the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The influence of sample geometry on the permeability of a porous sandstone
Although detailed guidelines exist for measuring the physical and mechanical properties of laboratory rock samples, guidelines for laboratory measurements of permeability are sparse. Provided herein are gas permeability measurements of cylindrical samples of Darley Dale sandstone (with a connected porosity of 0.135 and a pore and grain size of 0.2–0.3 mm) with different diameters (10, 20, and 25 mm) and lengths (from 60 to 10 mm), corresponding to aspect (length ∕ diameter) ratios between 6.2 and 0.4. These data show that, despite the large range in sample length, aspect ratio, and bulk volume (from 29.7 to 1.9 cm3), the permeabilities of the Darley Dale sandstone samples are near identical (3– m2). The near-identical permeability of these samples is considered the consequence of the homogeneous porosity structure typical of porous sandstones and the small grain and pore size of Darley Dale sandstone with respect to the minimum tested diameter and length (both 10 mm). Laboratory permeability measurements on rock samples with inhomogeneous porosity structures or with larger grain and pore sizes may still provide erroneous values if their length, diameter, and/or aspect ratio is low. Permeability measurements on rocks with vastly different microstructural properties should now be conducted in a similar manner to help develop detailed guidelines for laboratory measurements of permeability.
- Article
(7496 KB) - Full-text XML
- BibTeX
- EndNote
Suggested methods and instruments exist for measuring the physical and mechanical properties of rock, such as uniaxial compressive strength and fracture toughness. For example, the guidelines presented by the International Society for Rock Mechanics (ISRM; https://www.isrm.net/, last access: February 2019) and the American Society for Testing and Materials (ASTM; https://www.astm.org/, last access: February 2019) are often quoted in experimental papers to assure the community that the measurements were conducted according to a strict standard. The benefits of such practices are that published experimental data are (1) of a high standard and (2) can be compared from one publication to another. However, although most laboratory studies of permeability describe their methods in detail, there is no community consensus on how such measurements ought to be performed.
Permeability is a measure of the ability of a material to transmit fluids (Guéguen and Palciauskas, 1994). The permeability of crustal rocks therefore controls the movement of fluids and distribution of pore pressure in the Earth's crust. As a result, permeability is thought to exert an influence over the recurrence of earthquakes (e.g. Sibson, 1992; Caine et al., 1996; Faulkner et al., 2010) and volcanic eruptions (e.g. Eichelberger et al., 1986; Melnik et al., 2005; Mueller et al., 2008; Farquharson et al., 2017; Cassidy et al., 2018), as well as the distribution of ores (e.g. Rowland and Simmons, 2012), the productivity of geothermal reservoirs (e.g. Grant et al., 2013), and the suitability and long-term integrity of CO2 storage sites (e.g. Wollenweber et al., 2010).
The permeability of rocks is measured in the laboratory using different methods (steady-state method, transient- or pulse-decay method (e.g. Brace et al., 1968; Mueller et al., 2005), and the oscillating pore pressure method (e.g. Kranz et al., 1990; Fischer and Paterson, 1992)), under different conditions (confining pressure (e.g. Brace et al., 1968; David et al., 1994; Nara et al., 2011) and temperature (e.g. Morrow et al., 2001; Kushnir et al., 2017)), using different pore fluids (liquid water and gas (e.g. Tanikawa and Shimamoto, 2009; Heap et al., 2018)), and on samples with different geometries (shape, length, and diameter). Different methods and different conditions are used to suit the nature of the rock samples tested and the goal of a particular study. For example, it is impracticable on laboratory timescales to measure low-permeability samples using the steady-state method, and high pressures are required when studying the permeability structure of the crust. Clearly, guidelines for measuring permeability in the laboratory cannot demand that all values are measured using the same technique and under the same conditions. However, it is appropriate to form a community consensus as to the factors common to these studies, such as recommendations as to the sample geometry, how a sample is dried (for measurements of gas permeability) or saturated (for measurements of water permeability) prior to measurement, how long a sample should be left at a certain pressure increment before a measurement is taken, which pore fluid should be used, and whether a confining pressure is required to prevent pore fluid from passing between the sample and the sample jacket. The aspect tackled in this study is sample geometry. For example, when rock samples are rare, small, and/or oddly shaped, permeability is sometimes measured on samples with geometries that may not be considered entirely appropriate. A minimum aspect ratio of unity is often anecdotally quoted for laboratory measurements of permeability but, to the author's knowledge, no experimental data exist to confirm or deny this rule of thumb. Using cylindrical core samples of a widely used porous sandstone, the goal of this contribution is to better understand the influence of sample geometry on laboratory measurements of permeability.
Darley Dale sandstone (Fig. 1), a feldspathic sandstone from Derbyshire (England), was chosen for this study due to its wide use in laboratory studies (e.g. Read et al., 1995; Ayling et al., 1995; Zhu and Wong, 1997; Wong et al., 1997; Baud et al., 2000, 2004; Wu et al., 2000; Heap et al., 2009). Darley Dale sandstone has a connected porosity of 0.135 and an average pore and grain size of 0.2–0.3 mm (Fig. 1). The mineral composition of Darley Dale sandstone (estimated from a thin section) is 69 % quartz, 26 % feldspar, 3 % clay, and 2 % mica (Heap et al., 2009).

Figure 1Microscopic image of Darley Dale sandstone, taken in plane polarized light using an optical microscope.
Three cylindrical core samples, of diameters 10, 20, and 25 mm, were cored from the same block and in the same direction and were cut and their ends ground flat and parallel to a nominal length of 60 mm. The three samples were then washed (to remove any water-soluble grinding fluid) and dried in a vacuum oven at 40 ∘C for at least 48 h. The permeabilities of the three samples were then measured as outlined below. Once measured (each sample was measured at least twice; an average of these values is presented herein), the length of each of the samples was reduced by 5 mm and the samples were washed, dried, and permeability was re-measured. This process was continued until the samples were 10 mm long (although the 10 mm diameter sample broke as its length was reduced from 20 to 15 mm). When the 20 mm diameter sample reached a length of 40 mm, five measurements of permeability were performed to ascertain measurement precision. The repeated use of the same three samples, as opposed to >30 unique samples, was an attempt to avoid permeability variability associated with natural sample heterogeneity.
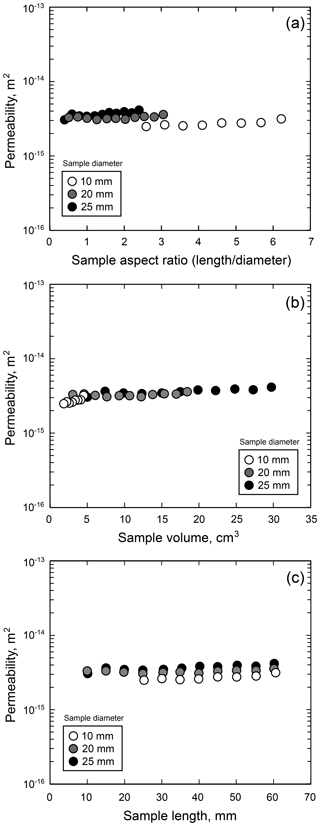
Permeability was measured using a benchtop gas (nitrogen) permeameter (Fig. 2; Farquharson et al., 2016; Heap and Kennedy, 2016) using the steady-state flow method (selected due to the reasonably high permeability of Darley Dale sandstone). All permeability measurements were conducted under a confining pressure, Pc, of 1 MPa and under ambient laboratory temperatures. A confining pressure of 1 MPa was used to prevent gas from passing between the sample and the rubber jacket (Fig. 2). Samples were left at 1 MPa for 1 h prior to measurement to allow for microstructural equilibrium.
Figure 2Schematic of the benchtop gas permeameter used for this study (modified from Farquharson et al., 2016; Heap and Kennedy, 2016).
Volumetric flow rate, Qv, measurements were taken (using a Bronkhorst gas flowmeter with a maximum flow rate of 50 mL min−1 and a precision of 0.005 mL min−1) for six different pressure differentials, ΔP (defined here as the upstream pore fluid pressure, Pu, minus the downstream pore fluid pressure, Pd). In the permeameter used for this study (Fig. 2), Pd is simply the atmospheric pressure (taken here to be 101 325 Pa). Values of ΔP were typically between 0.05 and 0.2 MPa (measured using a pressure transducer with a precision of 5 Pa), equating to flow rates between 5 and 45 mL min−1 (depending on the radius of the sample). Flow rates, and their corresponding pressure differentials, were recorded only when these values were constant. Assuming laminar flow, the permeability, kD, was then calculated for each ΔP using the following relation:
where μ is the viscosity of the pore fluid (taken as the viscosity of nitrogen at 20 ∘C Pa s), Pm is the mean pore fluid pressure (i.e. (), and A and L are the sample cross-sectional area and length, respectively. Sample lengths and diameters were measured using digital callipers (with a precision of 0.005 mm).
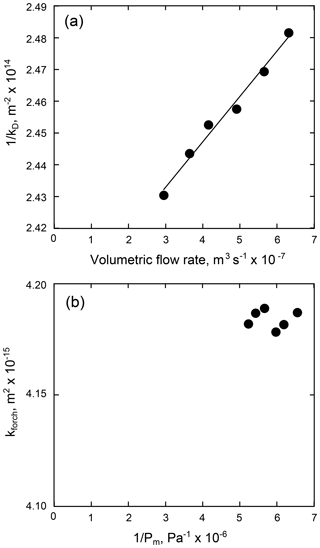
Figure 3(a) The reciprocal of Darcian permeability, kD, as a function of volumetric flow rate (for the sample 25 mm in diameter and 60 mm in length). The data can be well described by a positive linear slope: the Forchheimer correction is therefore needed. (b) The Forchheimer-corrected permeability as a function of the reciprocal of the mean pore fluid pressure (for the sample 25 mm in diameter and 60 mm in length; the same experiment shown in panel a). Since these data cannot be well described by a positive linear slope, no Klinkenberg correction is required.
The reason for calculating kD for different values of ΔP is to assess the Darcian permeability (Eq. 1) for fluid-flow-related artefacts: gas slip along flow channel walls (i.e. the Klinkenberg effect; Klinkenberg, 1941) and/or turbulent flow (i.e. the Forchheimer effect; Forchheimer, 1901). To check whether the Forchheimer correction is required, 1∕kD is plotted for each ΔP as a function of Qv. The Forchheimer correction is deemed necessary if these data are well described by a positive linear relationship (an example is shown in Fig. 3a; these data highlight that a Forchheimer correction is needed). The Forchheimer-corrected permeability is taken as the inverse of the y intercept of the best-fit linear regression of this positive linear relationship. If the Forchheimer correction is required, the data are then checked for the Klinkenberg correction. To do this, kforch is calculated for each ΔP using
where ξ, not strictly needed in this analysis, is the slope of the plot of 1∕kD as a function of Qv. kforch is then assessed as a function of 1∕Pm. The Klinkenberg correction is necessary if these data are well described by a positive linear relationship, and the true permeability is taken as the y intercept of the best-fit linear regression of the data. If the data on the plot of kforch as a function of 1∕Pm cannot be described by a positive linear slope, as in the example shown in Fig. 3b, then the true permeability is taken as the inverse of the y intercept of the best-fit linear regression on the graph of 1∕kD as a function of Qv (i.e. the best-fit linear regression shown in Fig. 3a). In the absence of a Forchheimer correction, the need for a Klinkenberg correction is determined by assessing kD as a function of 1∕Pm. A Klinkenberg correction is required if these data can be well described by a positive linear relationship. If required, the true sample permeability is given by the y intercept of the best-fit linear regression on the plot of kD as a function of 1∕Pm. kD is taken as the true permeability if no corrections are required and is given by the slope of the graph of Qv as a function of ΔP multiplied by the mean pore fluid pressure Pm. For the data collected for this study, either no correction or the Forchheimer correction was needed (see Table 1). The Klinkenberg correction was not required for any of the measurements (Table 1). More information on these methods can be found in Heap et al. (2017) and Kushnir et al. (2018).
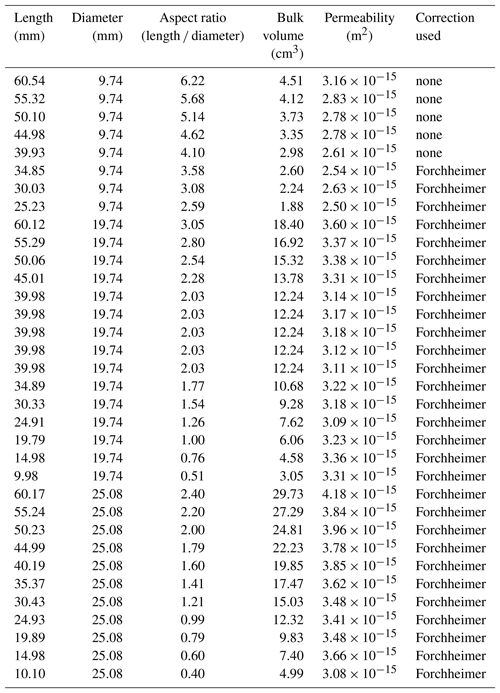
Plots of permeability as a function of sample aspect (length ∕ diameter) ratio, bulk sample volume, and sample length are provided in Fig. 4a, b, and c, respectively. These data show that, regardless of sample aspect ratio, volume, and length, the permeability of the measured Darley Dale sandstone samples did not differ significantly from 3 to m2 (Fig. 4; Table 1). The five measurements performed on the sample 20 mm in diameter and 40 mm in length, to ascertain measurement precision, yielded permeability values of , , , , and m2 (Table 1) (standard deviation of m2) and therefore highlight the high precision of the measurements presented.
Using cylindrical core samples of a widely used porous sandstone, the aim of this study was to better understand the influence of sample geometry on laboratory measurements of permeability. It is often anecdotally considered that an aspect ratio of unity is the minimum for reliable estimates of permeability. Here it is shown that, for Darley Dale sandstone, laboratory measurements of permeability yield the same value over a wide range of sample aspect ratios (from 6.2 and 0.4; Fig. 4a), including aspect ratios below unity, bulk volumes (from 29.7 to 1.9 cm3; Fig. 4b), and sample lengths (from 60 to 10 mm; Fig. 4c). It is likely that this is the result of the small pore and grain size (0.2–0.3 mm; Fig. 1) with respect to the minimum tested length ∕ diameter (10 mm) and the homogenous porosity structure of Darley Dale sandstone (Fig. 1). This result is of interest to those studying the permeability of porous sandstones, as it adds confidence to measurements conducted on samples with a small diameter, length, and/or volume. For example, since X-ray-computed tomography is often performed on small-diameter cores, permeability modelling using images of these cores could be confidently verified using laboratory measurements on the same cores (e.g. Fredrich et al., 2006). Based on the small pore size and homogenous pore structure of Darley Dale sandstone, core samples smaller than those measured herein (e.g. samples with diameters and/or lengths of 2 or 3 mm) may be sufficient to obtain reliable values of permeability. However, samples that contain, for example, very large pores or inhomogeneously connected porosity structures may still provide erroneous values of permeability if their lengths, diameters, and/or aspect ratios are low. Examples of rocks that are often characterized by complex microstructures include volcanic rocks (e.g. Farquharson et al., 2015; Colombier et al., 2017). Permeability measurements on rocks with vastly different microstructural properties should now be conducted in a similar manner to help develop detailed guidelines, such as a minimum microstructural feature (grain size or pore size) to sample diameter or length ratio, for laboratory measurements of permeability.
The data collected for this study are available in Table 1.
The author declares that there is no conflict of interest.
Philip Meredith kindly furnished the block of Darley Dale sandstone. Jamie
Farquharson and Alex Kushnir are thanked for their role in the development of
the benchtop permeameter. Alex Kushnir and Fabian Wadsworth are thanked for
proofreading the manuscript.
Edited by: Günter Kargl
Reviewed by: Mathieu Colombier and Audrey Ougier-Simonin
Ayling, M. R., Meredith, P. G., and Murrell, S. A.: Microcracking during triaxial deformation of porous rocks monitored by changes in rock physical properties, I. Elastic-wave propagation measurements on dry rocks, Tectonophysics, 245, 205–221, https://doi.org/10.1016/0040-1951(94)00235-2, 1995.
Baud, P., Zhu, W., and Wong, T.-f.: Failure mode and weakening effect of water on sandstone, J. Geophys. Res., 105, 16371–16389, https://doi.org/10.1029/2000JB900087, 2000.
Baud, P., Klein, E., and Wong, T.-F.: Compaction localization in porous sandstones: spatial evolution of damage and acoustic emission activity, J. Struct. Geol., 26, 603–624, https://doi.org/10.1016/j.jsg.2003.09.002, 2004.
Brace, W., Walsh, J. B., and Frangos, W. T.: Permeability of granite under high pressure, J. Geophys. Res., 73, 2225–2236, https://doi.org/10.1029/JB073i006p02225, 1968.
Caine, J. S., Evans, J. P., and Forster, C. B.: Fault zone architecture and permeability structure, Geology, 24, 1025–1028, https://doi.org/10.1130/0091-7613(1996)024<1025:FZAAPS>2.3.CO;2, 1996.
Cassidy, M., Manga, M., Cashman, K., and Bachmann, O.: Controls on explosive-effusive volcanic eruption styles, Nat. Commun., 9, 2839, https://doi.org/10.1038/s41467-018-05293-3, 2018.
Colombier, M., Wadsworth, F. B., Gurioli, L., Scheu, B., Kueppers, U., Di Muro, A., and Dingwell, D. B.: The evolution of pore connectivity in volcanic rocks, Earth Planet. Sc. Lett., 462, 99–109, https://doi.org/10.1016/j.epsl.2017.01.011, 2017.
David, C., Wong, T.-F., Zhu, W., and Zhang, J.: Laboratory measurement of compaction-induced permeability change in porous rocks: Implications for the generation and maintenance of pore pressure excess in the crust, Pure Appl. Geophys., 143, 425–456, https://doi.org/10.1007/BF00874337, 1994.
Eichelberger, J. C., Carrigan, C. R., Westrich, H. R., and Price, R. H.: Non-explosive silicic volcanism, Nature, 323, 598–602, https://doi.org/10.1038/323598a0, 1986.
Farquharson, J., Heap, M. J., Varley, N. R., Baud, P., and Reuschlé, T.: Permeability and porosity relationships of edifice-forming andesites: a combined field and laboratory study, J. Volcanol. Geoth. Res., 297, 52–68, https://doi.org/10.1016/j.jvolgeores.2015.03.016, 2015.
Farquharson, J. I., Heap, M. J., Lavallée, Y., Varley, N. R., and Baud, P.: Evidence for the development of permeability anisotropy in lava domes and volcanic conduits, J. Volcanol. Geoth. Res., 323, 163–185, https://doi.org/10.1016/j.jvolgeores.2016.05.007, 2016.
Farquharson, J. I., Wadsworth, F. B., Heap, M. J., and Baud, P.: Time-dependent permeability evolution in compacting volcanic fracture systems and implications for gas overpressure, J. Volcanol. Geoth. Res., 339, 81–97, https://doi.org/10.1016/j.jvolgeores.2017.04.025, 2017.
Faulkner, D. R., Jackson, C. A. L., Lunn, R. J., Schlische, R. W., Shipton, Z. K., Wibberley, C. A. J., and Withjack, M. O.: A review of recent developments concerning the structure, mechanics and fluid flow properties of fault zones, J. Struct. Geol., 32, 1557–1575, https://doi.org/10.1016/j.jsg.2010.06.009, 2010.
Fischer, G. J. and Paterson, M. S.: Measurement of Permeability and Storage Capacity in Rocks During Deformation at High Temperature and Pressure, in: Fault Mechanics and Transport Properties of Rocks, Academic Press, 213–252, 1992.
Forchheimer, P.: Wasserbewegung durch boden, Z. Ver. Dtsch. Ing., 45, 1782–1788, 1901.
Fredrich, J. T., DiGiovanni, A. A., and Noble, D. R.: Predicting macroscopic transport properties using microscopic image data, J. Geophys. Res., 111, B03201, https://doi.org/10.1029/2005JB003774, 2006.
Grant, M., Donaldson, I. G., and Bixley, P. F.: Geothermal Reservoir Engineering, Academic Press, 2013.
Guéguen, Y. and Palciauskas, V.: Introduction to the Physics of Rocks, Princeton University Press, Princeton, USA, 1994.
Heap, M. J. and Kennedy, B. M.: Exploring the scale-dependent permeability of fractured andesite, Earth Planet. Sc. Lett., 447, 139–150, https://doi.org/10.1016/j.epsl.2016.05.004, 2016.
Heap, M. J., Baud, P., Meredith, P. G., Bell, A. F., and Main, I. G.: Time-dependent brittle creep in Darley Dale sandstone, J. Geophys. Res., 114, B07203, https://doi.org/10.1029/2008JB006212, 2009.
Heap, M. J., Kushnir, A. R., Gilg, H. A., Wadsworth, F. B., Reuschlé, T., and Baud, P.: Microstructural and petrophysical properties of the Permo-Triassic sandstones (Buntsandstein) from the Soultz-sous-Forêts geothermal site (France), Geothermal Energy, 5, 26, https://doi.org/10.1186/s40517-017-0085-9, 2017.
Heap, M. J., Reuschlé, T., Farquharson, J. I., and Baud, P.: Permeability of volcanic rocks to gas and water, J. Volcanol. Geoth. Res., 354, 29–38, https://doi.org/10.1016/j.jvolgeores.2018.02.002, 2018.
Klinkenberg, L. J.: The permeability of porous media to liquids and gases, in: Drilling and production practice, American Petroleum Institute, New York, USA, 1941.
Kranz, R. L., Saltzman, J. S., and Blacic, J. D.: Hydraulic diffusivity measurements on laboratory rock samples using an oscillating pore pressure method, Int. J. Rock Mech. Min., 27, 345–352, https://doi.org/10.1016/0148-9062(90)92709-N, 1990.
Kushnir, A. R. L., Martel, C., Champallier, R., and Wadsworth, F. B.: Permeability evolution in variably glassy basaltic andesites measured under magmatic conditions, Geophys. Res. Lett., 44, 10262–10271, https://doi.org/10.1002/2017GL074042, 2017.
Kushnir, A. R. L., Heap, M. J., and Baud, P.: Assessing the role of fractures on the permeability of the Permo-Triassic sandstones at the Soultz-sous-Forêts (France) geothermal site, Geothermics, 74, 181–189, https://doi.org/10.1016/j.geothermics.2018.03.009, 2018.
Melnik, O., Barmin, A. A., and Sparks, R. S. J.: Dynamics of magma flow inside volcanic conduits with bubble overpressure buildup and gas loss through permeable magma, J. Volcanol. Geoth. Res., 143, 53–68, https://doi.org/10.1016/j.jvolgeores.2004.09.010, 2005.
Morrow, C. A., Moore, D. E., and Lockner, D. A.: Permeability reduction in granite under hydrothermal conditions, J. Geophys. Res., 106, 30551–30560, https://doi.org/10.1029/2000JB000010, 2001.
Mueller, S., Melnik, O., Spieler, O., Scheu, B., and Dingwell, D. B.: Permeability and degassing of dome lavas undergoing rapid decompression: an experimental determination, B. Volcanol., 67, 526–538, https://doi.org/10.1007/s00445-004-0392-4, 2005.
Mueller, S., Scheu, B., Spieler, O., and Dingwell, D. B.: Permeability control on magma fragmentation, Geology, 36, 399–402, https://doi.org/10.1130/G24605A.1, 2008.
Read, M. D., Ayling, M. R., Meredith, P. G., and Murrell, S. A.: Microcracking during triaxial deformation of porous rocks monitored by changes in rock physical properties, II. Pore volumometry and acoustic emission measurements on water-saturated rocks, Tectonophysics, 245, 223–235, https://doi.org/10.1016/0040-1951(94)00236-3, 1995.
Rowland, J. V. and Simmons, S. F.: Hydrologic, magmatic, and tectonic controls on hydrothermal flow, Taupo Volcanic Zone, New Zealand: Implications for the formation of epithermal vein deposits, Econ. Geol., 107, 427–457, https://doi.org/10.2113/econgeo.107.3.427, 2012.
Sibson, R. H.: Implications of fault-valve behaviour for rupture nucleation and recurrence, Tectonophysics, 211, 283–293, https://doi.org/10.1016/0040-1951(92)90065-E, 1992.
Tanikawa, W. and Shimamoto, T.: Comparison of Klinkenberg-corrected gas permeability and water permeability in sedimentary rocks, Int. J. Rock Mech. Min., 46, 229–238, https://doi.org/10.1016/j.ijrmms.2008.03.004, 2009.
Wollenweber, J., Alles, S., Busch, A., Krooss, B. M., Stanjek, H., and Littke, R.: Experimental investigation of the CO2 sealing efficiency of caprocks, Int. J. Greenh. Gas Con., 4, 231–241, https://doi.org/10.1016/j.ijggc.2010.01.003, 2010.
Wong, T.-F., David, C., and Zhu, W.: The transition from brittle faulting to cataclastic flow in porous sandstones: Mechanical deformation, J. Geophys. Res., 102, 3009–3025, https://doi.org/10.1029/96JB03281, 1997.
Wu, X. Y., Baud, P., and Wong, T.-f.: Micromechanics of compressive failure and spatial evolution of anisotropic damage in Darley Dale sandstone, Int. J. Rock Mech. Min., 37, 143–160, https://doi.org/10.1016/S1365-1609(99)00093-3, 2000.
Zhu, W. and Wong, T.-f.: The transition from brittle faulting to cataclastic flow: Permeability evolution, J. Geophys. Res., 102, 3027–3041, https://doi.org/10.1029/96JB03282, 1997.