Managing data of sensor-equipped transportation networks using graph databases

In this paper, we are concerned with data pertinent to transportation networks, which model situations in which objects move along a graph-like structure. We assume that these networks are equipped with sensors that monitor the network and the objects moving along it. These sensors produce time series data, resulting in sensor networks. Examples are river, road, and electricity networks.

Geographical information systems are used to gather, store, and analyse data, and we focus on these tasks in the context of data emerging from transportation networks equipped with sensors. While tailored solutions exist for many contexts, they are limited for sensor-equipped networks at this moment. We view time series data as temporal properties of the network and approach the problem from the viewpoint of property graphs. In this paper, we adapt and extend the theory of the existing property graph databases to model spatial networks, where nodes and edges can contain temporal properties that are time series data originating from the sensors. We propose a language for querying these property graphs with time series, in which time series and measurement patterns may be combined with graph patterns to describe, retrieve, and analyse real-life situations. We demonstrate the model and language in practice by implementing both in Neo4j and explore questions hydrology researchers pose in the context of the Internet of Water, including salinity analysis in the Yser river basin.

1 Introduction

Transportation networks are a common research subject. These networks range from river networks that transport water and road networks that transport vehicles to heat or electricity networks that transport energy. A transportation network is characterised by having a stable topology – that is, the connectivity between nodes does not change often – and objects or substances move through the topology. The objects or substances are measured or tracked by some sort of sensor, and these sensors create time series data. Using graphs to model transportation networks is a common practice based on the connection information often arising from vector-based Geographical Information System (GIS) data. Because these sensors themselves do not move, the time series can be attributed to the nodes and edges representing the vector elements. In the networks, there are also static data, which can be represented as common properties in the graph, such as the IDs of the vector elements. As a result, researchers have to process property graphs with time series in the nodes and edges. This is different from the field of temporal graphs because nodes and edges are always considered present here. Only the properties can change through time, in which case a property is considered to have different values at different points in time. In contrast, most work about temporal graphs assumes that nodes and edges can be removed or added, resulting in graphs where nodes and edges are linked to validity time intervals.

With the rise of the Internet of Things, the number of sensors in transportation networks has grown considerably, and the rate at which these sensors produce data is increasing too (McCabe et al., 2017). Therefore, the time series can have a high resolution of data points. Nodes and edges are well-supported in graph databases, and query languages exist to process them. However, managing time series in graph databases is not trivial. Additional data structures are required to store the time series, and the existing query languages do not support time series to express constraints (Gamper and Dignös, 2020). Similarly, time series databases are well-established with their query languages to deal with the timestamps and values. However, adding the graph structure of the network is not supported. A system that fully integrates and supports both graph structures and time series data is missing.

In this work, we use an existing model for property graphs to create a property graph model that includes time series in nodes and edges. We leverage pattern matching, commonly used in the current graph language, to create a query language and logic that can answer queries over the proposed graph model. One crucial part is that, in the query language the temporal properties, with their timestamp–value pairs, can interact with the nodes, edges, and their static properties. The natural order present in the time series is built into the query language to simplify writing constraints in the queries. This provides tools for studying and transforming the data for advanced analysis. The proposed logic is well-suited to objectively describe and study problems or shortcomings in the model or query language. Next to the theory in this work, the usage of the model and implementation is demonstrated on a practical use case within the Internet of Water project where electrical conductivity data are analysed for the Flemish Yser river.

A very preliminary version of the theory, presented in this paper, was published in Bollen (2022), without a theoretical framework and implementation. We want to use the present work to develop the theoretical foundation and to show how it can be implemented. In addition, we discuss experiments and additional examples here.

In Sect. 2, we discuss the related work, and in Sect. 3 the theoretical model for property graphs with time series is given. Section 4 defines the logic for the proposed query language and shows how this language can be realised using the Graph Pattern Matching Language (GPML). The section ends with some application examples. In Sect. 5, we describe our implementation of the graph model and query language using Neo4j and Cypher together with an experiment based on the Internet of Water project. Sections 6 and 7 discuss the proposed model and query language and present our conclusion.

2 Existing work

There is a long-lasting overlap between geographical information systems and the field of data management, especially if physical networks are studied. Our sensor networks closely align with the definition of “geosensor networks” by Nittel (2017). She points out that data are often handled by domain scientists who need to work with the data, preferably without needing to know the lower-level details of data management. This is also demonstrated in practice by the research of Rodríguez-Alarcón and Lozano (2022) for river basins, Hornsby and King (2008) for traffic on road networks, and Gilbert et al. (2018) for electricity networks, where each network is a transportation network in our definition and is modelled using a graph. Especially in the case of studying rivers, a lot of work is happening in Belgium, where climate change has a big impact because of the increasing occurrences of extreme meteorological events (Brouwers et al., 2015). It is, therefore, not surprising to see parties involved in handling rivers joining forces and investing in full-stack approaches encompassing measuring, storing, analysing, and managing data, as in the Internet of Water project (https://www.internetofwater.be/wat-is-internet-of-water/, last access: 20 November 2024). In this context, colleagues also studied the river Scheldt (Bollen et al., 2023) but approached the transportation network by modelling it as an interval labelled graph. In this work, we want to focus more on the raw time series in the geographical context.

In recent years, two types of graphs, resource description framework (RDF) graphs and property graphs, have come to the foreground. For the latter, the recent definition used is the definition given by Angles (2018). Bonifati et al. (2018) give a slightly different definition of property graphs. Before that, other versions of graphs were used: for example, the weighted graph (Devienne and Lebegue, 1986). George and Shekhar (2018) use this model and define time-aggregated graphs. In a time-aggregated graph, the weight of nodes and edges can vary over time. An example is the travel time in a network. This is part of dynamic, or temporal, graphs where the study focuses on nodes and edges that exist during a certain time (Debrouvier et al., 2021). There are also advanced systems, for example GRADOOP by Rost et al. (2022), that incorporate scaling and many interaction possibilities. This field is still an active research domain, as the recently started project HyGrpah (https://hygraph.net/, last access: 20 November 2024) shows. Even though existing temporal graphs might be able to accommodate our case, a dedicated graph definition for a property graph where certain properties are time series is not available to the best of our knowledge.

One of the first publications regarding the underlying logic or calculus for graph query languages is by Cruz et al. (1987) from 1987 regarding a query language on graphs with recursion. In this work, the relational model is used to store data. An approach based on a graph model is called regular path expression and is described by Backofen (1993). These ideas have been extended to regular path queries in tandem with the evolution of the graph model itself (Angles and Gutiérrez, 2008). Since then, different papers have been published that further build on regular path queries. Angles et al. (2017) show how this all fits together in the query languages. In their vision, the two basic elements of the graph query language are graph patterns and navigational patterns. The evolution is summarised by Bonifati et al. (2018) as the existence of regular path queries (RPQs) and conjunctive graph queries (CQs), which, when taken together, make u the language of conjunctive regular path queries (CRPQs). Adding disjunction to CRPQ results in a more expressive query language called union conjunctive regular path queries (UCRPQs). When considering edge labels in two directions, the theory also talks about two-way regular path queries (2RPQs), conjunctive two-way regular path queries (C2RPQs), and union C2RPQs (Barceló Baeza, 2013). However, these language classes do not account for reasoning over the properties of graphs. To accommodate this, the class of regular property graph queries can be used based on regular property graph logic and regular property graph algebra (Bonifati et al., 2018).

Despite the history, practical query languages have only been implemented in recent years. In contrast to early graph interaction, which was mainly imperative API-like, recent query languages are declarative (API: Application Programming Interface). The most important existing languages are Cypher (OpenCypher and GQL), SPARQL, Gremlin, and GSQL. There is an effort to standardise the graph query languages, as was done for SQL. This new standard, called GQL, incorporates elements from (open)Cypher, G-core, PGQL, and Tigergraph's GSQL (https://www.gqlstandards.org/existing-languages, last access: 20 November 2024). As Deutsch et al. (2022) show, these languages, especially GQL and SPARQL, have a common base for matching graph patterns, and it is called Graph Pattern Matching Language (GPML). The theoretical foundation of GPML has been recently described by Francis et al. (2022). They provide a calculus that uses the same concepts as the regular property graph logic.

For time series, declarative time series query languages and imperative query approaches exist. An elaborate theory, as in the case of the graph databases, does not exist to the best of our knowledge. The first versions of the time series database InfluxDB (https://www.influxdata.com/products/influxdb/, last access: 22 November 2024) have the query language InfluxQL, which uses SQL-like syntax and describes the results of the query in a declarative format. Now, a new language is used, called Flux, which is an imperative language where time series form a source in transformations. In an extended version of PostgreSQL, using TimescaleDB (https://www.timescale.com, last access: 20 November 2024), time series can be queried using SQL. However, they treat time series as tabular data, and they do not exploit the order of the measurements in the time series induced by the natural order of time.

3 A data model for property graphs with time series

The property graph model is well-suited to model transportation networks, and various definitions of this model exist: for example, the property graph model definition of Angles (2018) and the definition of Bonifati et al. (2018). In this work, the latter is used because it aligns better with our applications. Our definition of the “property graph with time series” model adapts the definition of Bonifati et al. in the book Querying Graphs (Bonifati et al., 2018) and adds time series based on the idea of Llusà Serra et al. (2016).

Definition 3.1. Given are a set of values 𝒱, a finite set of labels ℒ, and a set of timestamps 𝒯 (equipped with a total (temporal) order ≤). Further, we assume that a set of property keys 𝒦 is given, with two disjoint subsets 𝒦_S (S stands for static) and 𝒦_T (T stands for temporal). The sets 𝒱, ℒ, 𝒯, and 𝒦 are assumed to be pairwise disjoint. Lastly, the set $\mathcal{M}\subseteq \mathcal{T}\times \mathcal{V}$ denotes the set of measurements which are (timestamp,value) pairs.

A property graph with time series is then defined to be a structure

$$G=(\mathcal{N},\mathcal{E},\mathit{\lambda },{\mathit{\upsilon }}_{\mathrm{S}},{\mathit{\upsilon }}_{\mathrm{T}}),$$

where

• 𝒩 is a finite set of nodes;

• ℰ is a set of directed edges, where each edge belongs to 𝒩×𝒩;¹

• $\mathit{\lambda }:\mathcal{N}\cup \mathcal{E}\to {\mathcal{P}}_{<\mathit{\omega }}\left(\mathcal{L}\right)$ is a partial function assigning to nodes and edges a finite set of labels (here, 𝒫_<ω(ℒ) denotes the set of all finite subsets of ℒ);

• ${\mathit{\upsilon }}_{\mathrm{S}}:(\mathcal{N}\cup \mathcal{E})\times {\mathcal{K}}_{\mathrm{S}}\to \mathcal{V}$ is a partial function assigning a value to a static property of nodes and edges; and

• ${\mathit{\upsilon }}_{\mathrm{T}}:(\mathcal{N}\cup \mathcal{E})\times {\mathcal{K}}_{\mathrm{T}}\to {\mathcal{P}}_{<\mathit{\omega }}\left(\mathcal{M}\right)$ is a partial function assigning a finite set of measurements to a temporal property of nodes and edges. We require that in such a set no timestamp appears twice, and we call the image of the function υ_T a time series. □

Now, we introduce our simplified fictitious running example of such a graph, which is used throughout this paper.

Example 3.1. Our example of a property graph with time series contains seven nodes that all have a numeric identifier from 1 to 7, and these make up the set of nodes 𝒩. In addition, there are edges that represent the connectivity of the network. The connectivity is chosen to be unidirectional to reflect a river-like transportation network. There are six edges in total, being $(\mathrm{1},\mathrm{3}),(\mathrm{2},\mathrm{3}),(\mathrm{3},\mathrm{4}),(\mathrm{4},\mathrm{5}),(\mathrm{6},\mathrm{5})$, and (5,7). A visual representation is shown in Fig. 1. Each edge is identified by a pair of node identifiers. All nodes and edges can have zero or multiple labels to categorise them. In this example, we label all nodes with the label point, and we label all edges with the label path. Each node and edge is assigned a name to demonstrate the static properties. For the nodes, this name corresponds to the letter “N” together with the identifier and for the edges “E” with a number. For example, node 1 has a static property with key name and value N1, thus (1,𝚗𝚊𝚖𝚎) is mapped to N1. The edge (1,3), together with name, is mapped to the value E1. All mappings for the static properties are listed below. The temporal properties form the last part of the example. They consist of a property key and a value. The property value is considered to be a time series, which is a set of (timestamp,value) pairs. The values in the time series can be almost anything, but in this example, we use numerical values. For example, for node 1 the mapping is

$$\begin{array}{rl}& (\mathrm{1},\mathtt{\text{water-level}})\mapsto \\ & \mathit{\left\{}\right(\mathtt{\text{2022-08-15T10:00}},\mathrm{14}),(\mathtt{\text{2022-08-15T11:00}},\mathrm{14}),\\ & (\mathtt{\text{2022-08-15T12:00}},\mathrm{13}),(\mathtt{\text{2022-08-15T13:00}},\mathrm{13}),\\ & (\mathtt{\text{2022-08-15T14:00}},\mathrm{12}),(\mathtt{\text{2022-08-15T15:00}},\mathrm{12})\mathit{\}},\end{array}$$

which means that there is a time series with six values on 15 August 2022 around noon. Next to the nodes, there are also edges that have a temporal property; the times series represents the travel time for an object travelling along that edge.

We remark that, in this example, the timestamps are behaving perfectly. That is, timestamps are spread evenly, and all time series use the same timestamps. This does not need to be the case, and in reality it probably will not be the case. However, the example is easier to understand by assuming these characteristics.

The complete formal description of the example is as follows, with the remark that in the time series, the timestamps are on 15 August 2022, but only the time is shown for readability.

• $\mathcal{N}=\mathit{\{}\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6},\mathrm{7}\mathit{\}}$;

• $\mathcal{E}=\mathit{\left\{}\right(\mathrm{1},\mathrm{3}),(\mathrm{2},\mathrm{3}),(\mathrm{3},\mathrm{4}),(\mathrm{4},\mathrm{5}),(\mathrm{6},\mathrm{5}),(\mathrm{6},\mathrm{7}\left)\mathit{\right\}}$;

• $\mathit{\lambda }=\mathit{\{}\mathrm{1}\mapsto \mathit{\{}\mathtt{\text{point}}\mathit{\}}$, 2↦{𝚙𝚘𝚒𝚗𝚝}, 3↦{𝚙𝚘𝚒𝚗𝚝}, 4↦{𝚙𝚘𝚒𝚗𝚝}, 5↦{𝚙𝚘𝚒𝚗𝚝}, 6↦{𝚙𝚘𝚒𝚗𝚝}, 7↦{𝚙𝚘𝚒𝚗𝚝}, $(\mathrm{1},\mathrm{3})\mapsto \mathit{\left\{}\mathtt{\text{path}}\mathit{\right\}}$, $(\mathrm{2},\mathrm{3})\mapsto \mathit{\left\{}\mathtt{\text{path}}\mathit{\right\}}$, $(\mathrm{3},\mathrm{4})\mapsto \mathit{\left\{}\mathtt{\text{path}}\mathit{\right\}}$, $(\mathrm{4},\mathrm{5})\mapsto \mathit{\left\{}\mathtt{\text{path}}\mathit{\right\}}$, $(\mathrm{6},\mathrm{5})\mapsto \mathit{\left\{}\mathtt{\text{path}}\mathit{\right\}}$, $(\mathrm{6},\mathrm{7})\mapsto \mathit{\left\{}\mathtt{\text{path}}\mathit{\right\}}\mathit{\}}$;

• υ_S={ $(\mathrm{1},\mathtt{\text{name}})\mapsto \mathtt{\text{N1}}$, $(\mathrm{2},\mathtt{\text{name}})\mapsto \mathtt{\text{N2}}$, (3,𝚗𝚊𝚖𝚎) ↦𝙽3, (4,𝚗𝚊𝚖𝚎) ↦𝙽4, (5,𝚗𝚊𝚖𝚎) ↦𝙽5, (6,𝚗𝚊𝚖𝚎) ↦𝙽6, $(\mathrm{7},\mathtt{\text{name}})\mapsto \mathtt{\text{N7}}$, $\left(\right(\mathrm{1},\mathrm{3}),\mathtt{\text{name}})\mapsto \mathtt{\text{E1}}$, $\left(\right(\mathrm{2},\mathrm{3}),\mathtt{\text{name}})\mapsto \mathtt{\text{E2}}$, $\left(\right(\mathrm{3},\mathrm{4}),\mathtt{\text{name}})\mapsto \mathtt{\text{E3}}$, $\left(\right(\mathrm{4},\mathrm{5}),\mathtt{\text{name}})\mapsto \mathtt{\text{E4}}$, $\left(\right(\mathrm{6},\mathrm{5}),\mathtt{\text{name}})\mapsto \mathtt{\text{E5}}$, $\left(\right(\mathrm{5},\mathrm{7}),\mathtt{\text{name}})\mapsto \mathtt{\text{E6}}\mathit{\}}$;

• υ_T={ $(\mathrm{1},\mathtt{\text{water-level}})\mapsto \mathit{\left\{}\right(\mathtt{\text{10:00}},\mathrm{14})$, (11:00,14), (12:00,13), (13:00,13), (14:00,12), (15:00,12)},
  $(\mathrm{2},\mathtt{\text{water-level}})\mapsto \mathit{\left\{}\right(\mathtt{\text{10:01}},\mathrm{15})$, (11:02,15), (12:01,15), (13:01,15), (14:00,15), (15:01,16)},
  $(\mathrm{3},\mathtt{\text{water-level}})\mapsto \mathit{\left\{}\right(\mathtt{\text{10:00}},\mathrm{14})$, (10:30,13), (11:00,14), (11:30,14), (12:00,14), (12:30,15), (13:00,14), (13:30,14), (14:00,13), (14:30,12), (15:00,13)},
  $(\mathrm{5},\mathtt{\text{water-level}})\mapsto \mathit{\left\{}\right(\mathtt{\text{10:00}},\mathrm{14})$, (11:00,14), (12:00,15), (13:00,15), (14:00,14), (15:00,14)},
  $(\mathrm{6},\mathtt{\text{water-level}})\mapsto \mathit{\left\{}\right(\mathtt{\text{10:00}},\mathrm{18})$, (11:00,18), (12:00,17), (13:00,18), (14:00,19), (15:00,19)},
  $(\mathrm{7},\mathtt{\text{water-level}})\mapsto \mathit{\left\{}\right(\mathtt{\text{10:00}},\mathrm{18})$, (11:00,17), (12:00,16), (13:00,17), (14:00,18), (15:00,18)},
  $\left(\right(\mathrm{3},\mathrm{4}),\mathtt{\text{travel-time}})\mapsto \mathit{\left\{}\right(\mathtt{\text{10:00}},\mathrm{3.10})$, (11:00,3.50), (12:00,3.49), (13:00,3.47), (14:00,3.46), (15:00,3.44)},
  $\left(\right(\mathrm{4},\mathrm{5}),\mathtt{\text{travel-time}})\mapsto \mathit{\left\{}\right(\mathtt{\text{10:00}},\mathrm{3.20})$, (11:00,3.15), (12:00,3.53), (13:00,3.51), (14:00,3.48), (15:00,3.46)}}.

This concludes our example, a visual representation of which is shown in Fig. 1.□

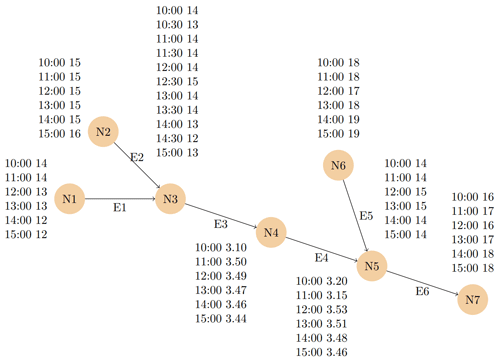
Figure 1 Visual graph representation of Example 3.1. The nodes are assigned a label point and the edges are labelled path; these labels are not shown. The timestamps also include a date, such as 15 August 2022, but it is not shown to reduce the clutter.

The total temporal order ≤ on the set 𝒯, assumed by Definition 3.1, induces a total order on the measurements in a time series. Indeed, the temporal order ≤ on 𝒯 induces an order (which we also denote by ≤) on ℳ, as follows: for $m_{\mathrm{1}},m_{\mathrm{2}}\in \mathcal{M}$, we define m₁≤m₂ if and only if τ(m₁)≤τ(m₂), where $\mathit{\tau }:\mathcal{M}\to \mathcal{T}$ is the projection on the time component (that is, τ returns the timestamp of a measurement). Furthermore, we define ν(m) to be the value of the measurement m (that is, its second component). In other words, a measurement m∈ℳ is the couple $\left(\mathit{\tau }\right(m),\mathit{\nu }(m\left)\right).$ The above order allows us to define a “next” relationship and a “previous” relationship between measurements in a time series. The definition of both is as follows. Given two measurements m₁ and m₂ in a time series s, m₂ is the next measurement after m₁, denoted $\mathit{next}(m_{\mathrm{2}},m_{\mathrm{1}},s)$ if and only if $m_{\mathrm{1}},m_{\mathrm{2}}\in s$, and m₁<m₂, and there is no measurement m in s with $m_{\mathrm{1}}<m<m_{\mathrm{2}}$ (here, < has the obvious meaning of ≤ but not equal). The definition for the previous measurement, $\mathit{previous}(m_{\mathrm{1}},m_{\mathrm{2}},s)$, then corresponds to $\mathit{next}(m_{\mathrm{2}},m_{\mathrm{1}},s)$. In the case that the second condition is dropped (that is, there might be another measurement between the other two), then we use predicates $\mathit{after}(m_{\mathrm{2}},m_{\mathrm{1}},s)$ to indicate that m₂ occurred after m₁ and $\mathit{before}(m_{\mathrm{2}},m_{\mathrm{1}},s)$ for the other case. In addition, we can extend this idea to define the first and last measurements. The first(m,s) and last(m,s) predicates are true for a measurement m, within a time series s, where there is no previous or next measurement for m in s, respectively.

4 A formal query language for property graphs with time series

4.1 Extending regular property graph logic

The concept of regular path queries is well-established and is an important concept (Nolé and Sartiani, 2016; Abiteboul and Vianu, 1999; and  Libkin and Vrgoč, 2012). For example, Cypher and GQL are based on the theory of regular property graph queries, described by Bonifati et al. (2018). These queries can be described using regular property graph logic or regular property graph algebra. To obtain a query language for property graphs with time series, we extend the regular property graph logic with elements to incorporate the time series. More specifically, we add the description of time series patterns for a temporal property in a node or an edge. The result is that the temporal properties are handled just like the nodes, edges, and properties. A query can contain node, edge, path, static property, and temporal property constraints that can be evaluated simultaneously. These constraints may depend on each other without the need for multiple queries.

We take the syntax and semantic definitions of regular property graph logic by Bonifati et al. (2018) and with it define our logic for property graph query language with time series, or GQL-TS logic. This is done by adding formal descriptions for temporal properties and querying them. We show how these logical elements can be realised as time series and measurement patterns in the Graph Pattern Matching Language. In the last part, example queries are given to demonstrate the different possibilities of our graph query language with time series, which we abbreviate as GQL-TS. The entire definition of regular property graph language is also included in this section. We add to it elements that deal with temporal properties – that is, time series – and how these are concatenated with the constraints. For the syntax and the semantics, the existing theory is first given, and we subsequently introduce the new elements added by us.

4.1.1 Syntax of GQL-TS logic

In this section, we give the syntactical definition of GQL-TS logic.

A query, expressed in GQL-TS logic, is conceived to take a property graph with time series (as presented in Definition 3.1) as input, and it takes the form of a set of non-recursive datalog-style rules. Each rule is a description of a sub-graph pattern or path of the input graph and is of the form

$$\begin{array}{}\text{(1)}& head\leftarrow bod{y}_{\mathrm{1}},\mathrm{\dots },bod{y}_m,constrain{t}_{\mathrm{1}},\mathrm{\dots },constrain{t}_n,\end{array}$$

which has a head predicate and, in the body, a sequence of body predicates, possibly in combination with additional constraints.

First, we need some additional notions and notations. We use 𝒩^var to denote the (possibly infinite) set of variables that represent nodes in a graph. Similarly, we have the set ℰ^var of variables that refer to edges in a graph. Finally, we assume an infinite set ℒ⁽²⁾ of fresh predicate names of arity 2.

We define the components of a query rule in GQL-TS logic. First, we define the form of the “head” of a rule, which either creates a new relation (called ℓ₂) or a result relation of some arity a.

Definition 4.1. The head of rule (1) either has the form

$${\mathrm{\ell }}_{\mathrm{2}}(x,y),$$

where ℓ₂∈ℒ⁽²⁾, $x,y\in {\mathcal{N}}^{var}$, or the form

$$\mathtt{\text{result}}(x_{\mathrm{1}},\mathrm{\dots },x_a),$$

with a≥1 and $x_{\mathrm{1}},\mathrm{\dots },x_a\in {\mathcal{N}}^{var}$. In the first case, we define $var\left(head\right):=\mathit{\{}x,y\mathit{\}}$, and in the second case, we define $var\left(head\right):=\mathit{\{}{x}_{\mathrm{1}},\mathrm{\dots },x_a\mathit{\}}$.□

Next, we define the form of the “body” components of a rule, which either uses an existing or previously created edge relation (called ℓ₂), computes the transitive closure of such an edge relation (denoted by ${\mathrm{\ell }}_{\mathrm{2}}^{*}$), or uses an existing unary node relation (called ℓ₁).

Definition 4.2. Each body_i in rule (1) has the form

• ℓ₂(x,y) 𝙰𝚂 e,

• ${\mathrm{\ell }}_{\mathrm{2}}^{*}(x,y)$, or

• ℓ₁(x),

where ${\mathrm{\ell }}_{\mathrm{2}}\in \mathit{\lambda }\left(\mathcal{E}\right)\cup {\mathcal{L}}^{\left(\mathrm{2}\right)}$ is of arity 2 and is not the predicate name used in the head of the rule, ℓ₁∈λ(𝒩) is of arity 1, $x,y\in {\mathcal{N}}^{var}$, and e∈ℰ^var. In the first case we define $var\left(bod{y}_i\right):=\mathit{\{}x,y,e\mathit{\}}$, in the second case we define $var\left(bod{y}_i\right):=\mathit{\{}x,y\mathit{\}}$, and in the third case we have var(body_i):={x}. □

Next, we define the form of the “constraint” components of a rule and distinguish between “static constraints” and “time series constraints”. In this definition, we need a set ℳ^var of measurement variables that range over measurements. When m∈ℳ^var, then m.value is a variable that ranges over values in 𝒱 and m.time is a variable that ranges over timestamps in 𝒯. Finally, we have a set Θ_v of binary operators (or relations) on the set of values 𝒱 and a set Θ_t of binary operators on 𝒯, to which the total order on timestamps ≤ is assumed to belong. Typically, we take Θ_v and Θ_t to be $\mathit{\{}=,\ne ,\le ,<,\ge ,>\mathit{\}}$.

Definition 4.3. Each constraint_j in rule (1) is either a static constraint or a time series constraint.

(1) Static constraints are of the form

• $x.{\mathit{\rho }}_{\mathrm{1}}{\mathit{\theta }}_{v}y.{\mathit{\rho }}_{\mathrm{2}}$,

• x.ρ₁ θ_v val, or

• x = y,

where $x,y\in {\mathcal{N}}^{var}\cup {\mathcal{E}}^{var}$, ${\mathit{\rho }}_{\mathrm{1}},{\mathit{\rho }}_{\mathrm{2}}\in {\mathcal{K}}_{\mathrm{S}}$, val∈𝒱, and θ_v is a binary operator from Θ_v. We define $var\left(constrain{t}_j\right)=\mathit{\{}x,y\mathit{\}}$ for the first and third case and var(constraint_j)={x} in the second case.

(2) Time series constraints are of the form

• $x.\mathit{\sigma }=[m_{\mathrm{1}},\mathrm{\dots },m_p]$, with p≥1;

• $x.\mathit{\sigma }=[m_{\mathrm{1}},\mathrm{\dots },m_k,*,m_{k+\mathrm{1}},\mathrm{\dots },m_p]$, with p≥2 and $\mathrm{1}\le k<p$;

• v₁ θ_v v₂; or

• t₁ θ_t t₂,

where $x\in {\mathcal{N}}^{var}\cup {\mathcal{E}}^{var}$, σ∈𝒦_T, and $m_{\mathrm{1}},\mathrm{\dots },m_p\in {\mathcal{M}}^{var}$ and where, furthermore,

• θ_v∈Θ_v, v₁, and v₂ are

  • values from 𝒱;

  • of the form m.value, with m∈ℳ^var; or

  • the result of a function (with co-domain in 𝒱) applied to value and time constants as well as variables.

• θ_t∈Θ_t, t₁, and t₂ are

  • timestamps from 𝒯;

  • of the form m.time, with m∈ℳ^var; or

  • the result of a function (with co-domain in 𝒯) applied to value and time constants and variables.
    □

We are ready to give the definition of a rule in GQL-TS logic.

Definition 4.4. A GQL-TS logic rule has the form

$$head\leftarrow bod{y}_{\mathrm{1}},\mathrm{\dots },bod{y}_m,constrain{t}_{\mathrm{1}},\mathrm{\dots },constrain{t}_n,$$

with m>0 and n≥0, where head, body_i, and constraint_j are as defined in Definitions 4.1, 4.2, and 4.3, with the additional restriction that

$$var\left(head\right)\subseteq \bigcup _{i=\mathrm{1}}^{m}var\left(bod{y}_i\right)\cup \bigcup _{j=\mathrm{1}}^{n}var\left(constrain{t}_j\right).\square$$

A query expressed in GQL-TS logic is then simply described by a (non-recursive) collection of GQL-TS logic rules. At least one rule in a query needs to have a special head result describing the final output of the query. We need to discuss the notion of the “dependency graph” of query Q such that we can define what is meant by non-recursive. In the rules of Q, several predicates may appear: some are existing node and edge predicates of the property graph with time series, and some are newly created predicates. In the dependency graph of Q, the predicates are nodes, and there is an edge from predicate ℓ to predicate ℓ^′ if ℓ appears in the head and ℓ^′ in the body of some rule in Q. When ℓ appears in the head and ℓ^′ in the body of some rule, we call ℓ^′ a “successor” of ℓ and ℓ a “predecessor” of ℓ^′. This dependency graph is called non-recursive if it is acyclic and recursive if it contains a cycle. With that, we can give the formal definition of a GQL-TS logic query.

Definition 4.5. A GQL-TS logic query is a finite non-empty and non-recursive set of rules such that at least one rule has a head predicate result and all result predicates have the same arity.□

When the predicate result appears more than once, we assume that this results in the union of the rules, as will be clear in the next section, where we define the semantics of GQL-TS logic.

Example 4.1. To make this more tangible, two example queries are now discussed. Take the graph in Example 3.1: on it, we want to find all nodes with the same temperature at the same moment in time as node N1. In other words, we need a query that expresses two node patterns where one matches node N1 and the other a node with the same value at the same moment for the temporal property “temperature”.

$$\begin{array}{rl}\mathtt{\text{result}}& (m,a,b)\leftarrow \\ & \mathtt{\text{point}}\left(n\right),\mathtt{\text{point}}\left(m\right),n.\mathtt{\text{name}}=\mathtt{\text{N1}},\\ & n.\mathtt{\text{temperature}}=\left[a\right],m.\mathtt{\text{temperature}}=\left[b\right],\\ & a.\mathit{value}=b.\mathit{value},a.\mathit{time}=b.\mathit{time},n.\mathit{name}\ne m.\mathit{name}\end{array}$$

First the head of the rule $\mathtt{\text{result}}(m,a,b)$ is given. It states that the query will return all matches for the variables m, a, and b, for which additional criteria are defined. Starting with the body predicates, 𝚙𝚘𝚒𝚗𝚝(n) and 𝚙𝚘𝚒𝚗𝚝(m), match a node with the label “point” to the node variables n and m. The node's name matched to n needs to be equal to N1, which is expressed by the constraint $n.\mathtt{\text{name}}=\mathtt{\text{N1}}$. This last part is already a constraint as given in Definition 4.3. The next four constraints focus on the temporal properties, with the first two matching a measurement a and b in the temporal node property temperature in node n and m, respectively. These measurements need to have the same value at the same moment in time, expressed by the constraints $a.\mathit{value}=b.\mathit{value}$ and $a.\mathit{time}=b.\mathit{time}$. Finally, the constraint $n.\mathit{name}\ne m.\mathit{name}$ is needed to prevent the query from matching the same node to m and n. This is done with the name in this case but can be realised with any node property that can differentiate any two nodes.

Edges and the temporal properties of those are the focus of the second example query. In the example graph, we want to find two consecutive edges where the travel time on the second edge (in direction) is lower than the travel time on the first edge.

$$\begin{array}{rl}\mathtt{\text{result}}& (e_{\mathrm{1}},e_{\mathrm{2}})\leftarrow \\ & \mathtt{\text{path}}(n,m)\text{ as }{e}_{\mathrm{1}},\mathtt{\text{path}}(o,p)\text{ as }{e}_{\mathrm{2}},m=o,\\ & e_{\mathrm{1}}.\mathtt{\text{travel-time}}=\left[a\right],e_{\mathrm{2}}.\mathtt{\text{travel-time}}=\left[b\right],\\ & a.\mathit{time}=b.\mathit{time},a.\mathit{value}<b.\mathit{value}\end{array}$$

This formal query example includes two edge variables in the header: e₁ and e₂. Here, two different body predicates are used, 𝚙𝚊𝚝𝚑(n,m) as e₁ and 𝚙𝚊𝚝𝚑(o,p) as e₂, that match edges with the label “path”. These predicates also explicitly link four node variables to the nodes that make up the edges. In this example, we named these variables n, m, o, and p. The constraints can be written using these variables, defining the requirements to which the matches must adhere. First, the constraint m=o ensures that the two edges are consecutive because the end node of the first edge needs to be the same as the start node of the second edge. Secondly, constraints $e_{\mathrm{1}}.\mathtt{\text{travel-time}}=\left[a\right]$ and $e_{\mathrm{2}}.\mathtt{\text{travel-time}}=\left[b\right]$ again match a measurement in each edge's temporal property “travel time”. These measurements have to adhere to the constraints expressed on the last line: $a.\mathit{time}=b.\mathit{time}$ and $a.\mathit{value}<b.\mathit{value}$, expressing the requirements for the values and timestamps.

4.1.2 Semantics of GQL-TS logic

In this section, we give the semantics of GQL-TS logic queries when applied to a property graph with time series. Two parts form the following semantics: (a) the bodies and constraints of rules are satisfied by an assignment, and (b) each valid assignment contributes elements to a set defined by the head of a rule. The first part will be called the satisfaction of rules, and the second part will be the evaluation of rules. We first define the rule evaluation and then discuss the satisfaction problem for the bodies and constraints.

Given a property graph with time series $G=(\mathcal{N},\mathcal{E},\mathit{\lambda },{\mathit{\upsilon }}_{\mathrm{S}},{\mathit{\upsilon }}_{\mathrm{T}})$, a query Q, expressed in GQL-TS logic, consists of a finite set of rules R_Q, where a rule r∈R_Q is a GQL-TS logic rule and where at least one rule in R_Q has $\mathtt{\text{result}}(x_{\mathrm{1}},\mathrm{\dots },x_a)$ as its head. We denote the predicate of the head of rule r by head(r).

When a rule r has head predicate ℓ=head(r), and only when the semantics of all predicates ℓ^′ that are successors of ℓ in the dependency graph of Q have been evaluated on G, we can define the semantics of the predicate ℓ on G. We remark that this recursive process stops since the dependency graph of Q is acyclic.

The evaluation of a rule r∈R_Q on G results in the creation of a c_r-ary relation, where c_r is the arity of ℓ=head(r). This c_r-ary relation is defined in terms of assignments of the form

$$\mathit{\mu }:{\mathcal{N}}^{var}\cup {\mathcal{E}}^{var}\cup {\mathcal{M}}^{var}\to \mathcal{N}\cup \mathcal{E}\cup \mathcal{M},$$

which assign identifiers to node, edge, and measurement variables. Suppose that rule r has the form $head\leftarrow bod{y}_{\mathrm{1}},\mathrm{\dots },bod{y}_m,constrain{t}_{\mathrm{1}},\mathrm{\dots },constrain{t}_n$; then we define Sat(r) to be the set of assignments μ for which

$$\begin{array}{rl}& G\vDash (bod{y}_{\mathrm{1}}\wedge \mathrm{\cdots }\wedge bod{y}_m\wedge constrain{t}_{\mathrm{1}}\wedge \mathrm{\cdots }\wedge \\ & constrain{t}_n\left)\right[\mathit{\mu }]\end{array}$$

in the usual sense used in predicate logic (for our specific constraints, in particular those on time series, we give the details below). If the head of r has the form $\mathrm{\ell }(x_{\mathrm{1}},\mathrm{\dots },x_{c_r})$, then the evaluation of the rule r on G is the set

$$\left[\right[r]{]}_G:=\mathit{\{}\left(\mathit{\mu }\right(x_{\mathrm{1}}),\mathrm{\dots },\mathit{\mu }(x_{c_r}\left)\right)\mid \mathit{\mu }\in Sat\left(r\right)\mathit{\}}.$$

The head $\mathrm{\ell }(x_{\mathrm{1}},\mathrm{\dots },x_{c_r})$ of rule r may appear in several rules of the query Q (possibly with other variable names). Then, we define the semantics of this predicate ℓ in G to be

$$\left[\right[\mathrm{\ell }]{]}_G:=\bigcup _{r\in R_Q,head\left(r\right)=\mathrm{\ell }}[\left[r\right]{]}_G.$$

The result of the evaluation of the query Q on the property graph with time series G is then defined to be the a-ary relation

$$\left[\right[Q]{]}_G:=\bigcup _{r\in R_Q,head\left(r\right)=\mathtt{\text{result}}}[\left[r\right]{]}_G.$$

What remains to be specified is the meaning of G⊧body_i[μ] and G⊧constraint_j[μ] for a body_i in a rule r (as in Definition 4.2) and constraint_j in a rule r (as in Definition 4.3).

Satisfaction of body predicates. We define the meaning of G⊧body_i[μ] for each of the various forms of body_i that we defined earlier in Definition 4.2.

A body predicate body_i in a rule r is satisfied by a mapping μ.

The following applies.

• If body_i is of the form ℓ₂(x,y) 𝙰𝚂 e and ℓ₂∈λ(ℰ), then G⊧(ℓ₂(x,y) as e)[μ] if an edge exists in ℰ such that $\mathit{\mu }\left(e\right)=\left(\mathit{\mu }\right(x),\mathit{\mu }(y\left)\right)\in \mathcal{E}$ and ℓ₂∈λ(μ(e)).

• If body_i is of the form ℓ₂(x,y) 𝙰𝚂 e and ℓ₂∈ℒ⁽²⁾, then G⊧(ℓ₂(x,y) 𝙰𝚂 e)[μ] if an edge exists in [[ℓ₂]]_G with $\mathit{\mu }\left(e\right)=\left(\mathit{\mu }\right(x),\mathit{\mu }(y\left)\right)\in \left[\right[{\mathrm{\ell }}_{\mathrm{2}}]{]}_G$.

• If body_i is of the form ${\mathrm{\ell }}_{\mathrm{2}}^{*}(x,y)$, an additional set is needed before we can define the satisfaction condition. For this purpose, we introduce the following notation:

  $$x\stackrel{\mathrm{\ell },G}{⟶}y,$$

  which expresses that the tuple (x,y) belongs to (1) the transitive closure of the edges in G with label ℓ when ℓ is an existing label in G or (2) the transitive closure of a newly created relation, labelled ℓ, when ℓ is not in the original graph G. The set $\left[\right[{\mathrm{\ell }}_{\mathrm{2}}^{*}]{]}_G$ is then defined as

  $$\mathit{\left\{}\right(x,x)\mid x\in \mathcal{N}\mathit{\}}\cup \mathit{\left\{}\right(x,y)\mid x,y\in \mathcal{N}\text{ and }x\stackrel{{\mathrm{\ell }}_{\mathrm{2}},G}{⟶}y\mathit{\}}.$$

  We want to remark that the meaning of this set has to be interpreted as “zero or more times an edge with label ℓ”. Therefore, the pairs $(x,x)\mid x\in \mathcal{N}$ are included to ensure that assignments where the edge occurs zero times are possible. Finally, $G\vDash \left({\mathrm{\ell }}_{\mathrm{2}}^{*}\right(x,y\left)\right)$ if $\left(\mathit{\mu }\right(x),\mathit{\mu }(y\left)\right)\in \left[\right[{\mathrm{\ell }}_{\mathrm{2}}^{*}]{]}_G$.

• If body_i is of the form ℓ₁(x) with ℓ₁∈λ(𝒩), then G⊧(ℓ₁(x)) if μ(x)∈𝒩 and ℓ₁∈λ(μ(x)).

Satisfaction of constraints. We define the meaning of G⊧constraint_j[μ], for each form of constraint_j that appears in Definition 4.3. For each of the comparison relations θ_v and θ_t, we also use this symbol for their interpretation in the structure G (abusing notation).

• If constraint_j is of the form $x.{\mathit{\rho }}_{\mathrm{1}}{\mathit{\theta }}_{v}y.{\mathit{\rho }}_{\mathrm{2}}$, then $G\vDash (x.{\mathit{\rho }}_{\mathrm{1}}{\mathit{\theta }}_{v}y.{\mathit{\rho }}_{\mathrm{2}})\left[\mathit{\mu }\right]$ if $\mathit{\mu }\left(x\right),\mathit{\mu }\left(y\right)\in \mathcal{N}\cup \mathcal{E}$ and ${\mathit{\upsilon }}_{\mathrm{S}}\left(\mathit{\mu }\right(x),{\mathit{\rho }}_{\mathrm{1}}){\mathit{\theta }}_v{\mathit{\upsilon }}_{\mathrm{S}}\left(\mathit{\mu }\right(y),{\mathit{\rho }}_{\mathrm{2}}))$.

• If constraint_j is of the form x.ρ₁ θ_v val, then G⊧(x.ρ₁ θ_v val)[μ] if $\mathit{\mu }\left(x\right)\in \mathcal{N}\cup \mathcal{E}$ and υ_S(μ(x),ρ₁) θ_v val.

• If constraint_j is of the form x = y, then G⊧(x = y)[μ] if μ(x)=μ(y).

For the constraints concerning the time series, two additional functions are assumed to exist. We assume a function exists, with co-domain in 𝒱, that takes as input value and time constants as well as variables. We denote this function with f_𝒱. Similarly, the function taking value and time constants as well as variables with co-domain 𝒯 is represented with f_𝒯.

• If the form of constraint_j is $x.\mathit{\sigma }=[m_{\mathrm{1}},\mathrm{\dots },m_p]$, then $G\vDash (x.\mathit{\sigma }=[m_{\mathrm{1}},\mathrm{\dots },m_p\left]\right)\left[\mathit{\mu }\right]$ if

  • 1.

    $\mathit{\mu }\left(x\right)\in \mathcal{N}\cup \mathcal{E}$,

  • 2.

    $\mathit{\left\{}\mathit{\mu }\right(m_{\mathrm{1}}),\mathrm{\dots },\mathit{\mu }(m_p\left)\mathit{\right\}}\subseteq {\mathit{\upsilon }}_{\mathrm{T}}\left(\mathit{\mu }\right(x),\mathit{\sigma })$, and

  • 3.

    for all m_l values with $\mathrm{1}\le l\le p$ μ(m_l)∈ℳ and $\mathit{next}\left(\mathit{\mu }\right(m_{l+\mathrm{1}}),\mathit{\mu }(m_l),{\mathit{\upsilon }}_{\mathrm{T}}(\mathit{\mu }\left(x\right),\mathit{\sigma }\left)\right)$ holds.

  We remark that if p=1, then next() cannot be satisfied and should be ignored (similarly, when l=p).

• If the form of constraint_j is $x.\mathit{\sigma }=[m_{\mathrm{1}},\mathrm{\dots },m_k,*,m_{k+\mathrm{1}},\mathrm{\dots },m_p]$, with p≥2 and $\mathrm{1}\le k<p$, then $G\vDash (x.\mathit{\sigma }=[m_{\mathrm{1}},\mathrm{\dots },m_k,*,m_{k+\mathrm{1}},\mathrm{\dots },m_p\left]\right)$ if

  • 1.

    $\mathit{\mu }\left(x\right)\in \mathcal{N}\cup \mathcal{E}$,

  • 2.

    $\mathit{\left\{}\mathit{\mu }\right(m_{\mathrm{1}}),\mathrm{\dots },\mathit{\mu }(m_p\left)\mathit{\right\}}\subseteq {\mathit{\upsilon }}_{\mathrm{T}}\left(\mathit{\mu }\right(x),\mathit{\sigma })$, and

  • 3.

    for all m_l values with $\mathrm{1}\le l\le p$ μ(m_l)∈ℳ and $\mathit{next}\left(\mathit{\mu }\right(m_{l+\mathrm{1}}),\mathit{\mu }(m_l),{\mathit{\upsilon }}_{\mathrm{T}}(\mathit{\mu }\left(x\right),\mathit{\sigma }\left)\right)$ holds, except for l=k, and then $\mathit{after}\left(\mathit{\mu }\right(m_{l+\mathrm{1}}),\mathit{\mu }(m_l),{\mathit{\upsilon }}_{\mathrm{T}}(\mathit{\mu }\left(x\right),\mathit{\sigma }\left)\right)$ holds.

The following applies.

• If constraint_j has the form v₁ θ_v v₂ and v₁ is of the form m.value and v₂∈𝒱, then G⊧(v₁ θ_v v₂)[μ] if μ(m)∈ℳ and ν(μ(m)) θ_v v₂.

• If constraint_j has the form v₁ θ_v v₂ and v₁ is the result of f_𝒱(m.time) with m∈ℳ^var and v₂∈𝒱, then G⊧(v₁ θ_v v₂)[μ] if μ(m)∈ℳ and f_𝒱(τ(μ(m))) θ_v v₂.

• If constraint_j has the form v₁ θ_v v₂ and v₁ and v₂ are value constants, the result of f_𝒱 applied to time constants, or the result of f_𝒱 after μ is applied to variables, then G⊧(v₁ θ_v v₂)[μ] if v₁ θ_v v₂.

The following applies.

• If constraint_j has the form is t₁ θ_t t₂ and t₁ is of the form m.time and t₂∈𝒯, then G⊧(t₁ θ_t t₂)[μ] if μ(m)∈ℳ and τ(μ(m)) θ_t t₂.

• If constraint_j has the form is t₁ θ_t t₂ and t₁ is the result of f_𝒯(m.value) with m∈ℳ^var, then G⊧(t₁ θ_t t₂)[μ] if μ(m)∈ℳ and f_𝒯(ν(μ(m))) θ_t t₂.

• If constraint_j has the form is t₁ θ_t t₂ and t₁ and t₂ are value constants, the result of f_𝒯 applied to value constants, or the result of f_𝒯 after μ is applied to variables, then G⊧(t₁ θ_t t₂)[μ] if t₁ θ_t t₂.

Example 4.2. In order to have a more practical understanding of the evaluation of the rules, the two queries introduced in Example 4.1 are evaluated here.

The first query contains one rule with head result that needs to be evaluated. This means that the evaluation of the query, denoted as [[Q]]_G, is given as ${\bigcup }_{r\in R_Q,head\left(r\right)=\mathtt{\text{result}}}\left[\right[r]{]}_G$. There is only one; therefore, the expression can be simplified to [[Q]]_G:=[[r]]_G, with r the rule as given in the example. The evaluation of the rule is defined as finding all possible mappings for identifiers to node, edge, and measurement variables that satisfy all the constraints in the rule. In general $\left[\right[r]{]}_G:=\mathit{\{}\left(\mathit{\mu }\right(x_{\mathrm{1}}),\mathrm{\dots },\mathit{\mu }(x_{c_r}\left)\right)\mid \mathit{\mu }\in Sat\left(r\right)\mathit{\}}$, and this results in $\left[\right[Q]{]}_G:=\mathit{\{}\left(\mathit{\mu }\right(n),\mathit{\mu }(m),\mathit{\mu }(a),\mathit{\mu }(b\left)\right)\mid \mathit{\mu }\in Sat\left(r\right)\mathit{\}}$ for this exact query, where the node variables n and m need to mapped, as well as the measurements variables a and b. To conclude the evaluation, each possible mapping with the graph needs to be considered. First, the node variables are mapped, and if there is a valid mapping considering the constraints, then the measurement variable mappings are tried. There are seven nodes in total, which yields 49 possible mappings. One possible mapping is n←2 and m←3, which already satisfies the predicates 𝚙𝚘𝚒𝚗𝚝(n) and 𝚙𝚘𝚒𝚗𝚝(m), but the constraint $n.\mathit{name}=\mathtt{\text{N1}}$ is not satisfied. Consequently, we can already see that only mapping where n←1 can satisfy the entire rule. Similarly, m←1 can never be a part of the mapping because it would violate constraint $n.\mathit{name}\ne m.\mathit{name}$. We are left with six possible mappings where either 2, 3, 4, 5, 6, or 7 is mapped to m. For each of these, we have to see if there is a valid mapping for a and b. The constraint $a.\mathit{time}=b.\mathit{time}$ reduces the number of possible mappings drastically. What remains is to see that $a.\mathit{value}=b.\mathit{value}$. The following mappings satisfy this constraint.

• m←2: none.

• m←3: $a\leftarrow (\mathtt{\text{10:00}},\mathrm{14})$, $b\leftarrow (\mathtt{\text{10:00}},\mathrm{14})$; $a\leftarrow (\mathtt{\text{11:00}},\mathrm{14})$, $b\leftarrow (\mathtt{\text{11:00}},\mathrm{14})$.

• m←4: none because there is already no mapping for b.

• m←5: $a\leftarrow (\mathtt{\text{10:00}},\mathrm{14})$, $b\leftarrow (\mathtt{\text{10:00}},\mathrm{14})$; $a\leftarrow (\mathtt{\text{11:00}},\mathrm{14})$, $b\leftarrow (\mathtt{\text{11:00}},\mathrm{14})$.

• m←6: none.

• m←7: none.

In total, four valid mappings can be found.

1. $\mathit{\mu }=(n\leftarrow \mathrm{1},m\leftarrow \mathrm{3},a\leftarrow (\mathtt{\text{10:00}},\mathrm{14}),b\leftarrow (\mathtt{\text{10:00}},\mathrm{14}\left)\right)$,

2. $\mathit{\mu }=(n\leftarrow \mathrm{1},m\leftarrow \mathrm{3},a\leftarrow (\mathtt{\text{11:00}},\mathrm{14}),b\leftarrow (\mathtt{\text{11:00}},\mathrm{14}\left)\right)$,

3. $\mathit{\mu }=(n\leftarrow \mathrm{1},m\leftarrow \mathrm{5},a\leftarrow (\mathtt{\text{10:00}},\mathrm{14}),b\leftarrow (\mathtt{\text{10:00}},\mathrm{14}\left)\right)$, or

4. $\mathit{\mu }=(n\leftarrow \mathrm{1},m\leftarrow \mathrm{5},a\leftarrow (\mathtt{\text{11:00}},\mathrm{14}),b\leftarrow (\mathtt{\text{11:00}},\mathrm{14}\left)\right)$.

This means that this query returns four answers when evaluated on the graph given in Example 3.1. Since the head of the rules includes only the variables m, a, and b, the actual result collection of the query is

$$\begin{array}{rl}& \mathit{\left\{}\right(\mathrm{3},(\mathtt{\text{10:00}},\mathrm{14}),(\mathtt{\text{10:00}},\mathrm{14})),(\mathrm{3},(\mathtt{\text{11:00}},\mathrm{14}),\\ & (\mathtt{\text{11:00}},\mathrm{14})),(\mathrm{5},(\mathtt{\text{10:00}},\mathrm{14}),(\mathtt{\text{10:00}},\mathrm{14})),\\ & (\mathrm{5},(\mathtt{\text{11:00}},\mathrm{14}),(\mathtt{\text{11:00}},\mathrm{14}\left)\right)\mathit{\}}.\end{array}$$

This nicely demonstrates how the variables denoted in the result() head define what is returned by the query.

Only the mappings for the variables and the final result are discussed for the second query. In theory, all possible mappings of edges need to be considered for e₁ and e₂. However, the constraint m=o only allows consecutive edges. In addition, the constraint with $e_{\mathrm{1}}.\mathtt{\text{travel-time}}=\left[a\right]$ and $e_{\mathrm{2}}.\mathtt{\text{travel-time}}=\left[b\right]$ quickly reduces the possible number of mappings to only one: $e_{\mathrm{1}}\leftarrow (\mathrm{3},\mathrm{4})$ and $e_{\mathrm{2}}\leftarrow (\mathrm{4},\mathrm{5})$. As last time, all possible measurements need to be matched, considering the constraints $a.\mathit{time}=b.\mathit{time}$ and $a.\mathit{value}<b.\mathit{value}$. Only one mapping with $a\leftarrow (\mathtt{\text{11:00}},\mathrm{3.50})$ and $b\leftarrow (\mathtt{\text{11:00}},\mathrm{3.15})$ is able to do this. Therefore, the result of this query contains only one entry: $\mathit{\left\{}\right((\mathrm{3},\mathrm{4}),(\mathrm{4},\mathrm{5})\left)\mathit{\right\}}$. We remark that, if other measurements in these temporal properties yielded a valid mapping, the result would remain the same since the union would eliminate the duplicate entry for e₁ and e₂. If the measurements themselves were included, then this would not happen.

4.2 Graph query language with time series

In this section, the GPML notation is extended with elements to describe time series with time series patterns consisting of measurement patterns. Important is that, in a time series pattern, two consecutive measurement patterns indicate that the measurements matched need to fulfil the next() relationship. We start with an introduction of the existing GPML notation of queries. These express graph patterns matching nodes and edges. The ability to express temporal properties in these nodes and edges is added by us in the subsequent subsection. First, the syntax of a measurement pattern is described. Afterwards, we demonstrate how these can be combined into a time series pattern, and finally, these time series patterns are linked with existing GPML notation. When all these elements are described, then we will discuss a set of example queries that demonstrate the use of the newly developed notation.

4.2.1 GPML introduction

To recap, we will first show some important notations of GPML. We refer to Deutsch et al. (2022) for a complete description of the notation. A pattern in GPML describes the structure to which sub-graphs need to adhere to be considered a match. Additional information, such as properties and labels, involves constraints added to the pattern.

A node is described by a set of round brackets, a possible name, and a label within the brackets separated by a colon. Property constraints can be expressed after the WHERE clause. The property key is written, followed by a constant or variable that constrains the property value. This is demonstrated in the following example.

    (a:point WHERE name = 'N1');

The pattern describes a node with label point and a property name that needs to have the value N1. Each node that matches the pattern is assigned to the variable a. We remark that a represents one node match at a time.

An edge is represented by two square brackets and an arrow. The pattern can contain a label, an edge type, a variable name, and properties. The notation for these three elements is exactly the same as for node patterns.

    ()-[b:path WHERE name = 'E3']->();

In this example, an edge is described with a type path, and it must have a property name, which should be equal to E3. The direction of the edge is indicated by the arrow to the right. The two () patterns describe the existence of a node with no additional requirements, but any valid node pattern is allowed. Similar to the empty nodes, the most basic edge pattern between two nodes is -[]-, which only requires the existence of an edge with no additional constraints. Together with two blank nodes, ()-[]-(), the pattern would produce all matches of two nodes with an edge between them. An edge can be matched zero or multiple times by using the Kleene star or one of the other repetition notations.

Finally, a query consists of node and edge patterns, preceded by the keyword MATCH and followed by an optional keyword WHERE, after which additional constraints can be written using the variables that are used in the node and edge patterns.

4.2.2 Measurement pattern

We consider a measurement a timestamp–value pair. A measurement pattern <m> describes a measurement, where m.timestamp represents the timestamp component and m.value the value component. For example, if m is matched to (2022-08-15T13:00,17), then m.timestamp = 2022-08-15T13:00 and m.value = 17.

4.2.3 Time series pattern

A time series consists of one or multiple measurements with an order on their timestamp. Therefore, a time series pattern is one or multiple measurement patterns that describe a subset of the time series together. Two concatenated measurement patterns express two measurements for which the next predicate holds. This means that for the pattern <m><n> and series s, $\mathit{next}(n,m,s)$ is true (or $\mathit{previous}(m,n,s)$).

In GPML, some quantifiers allow patterns to be repeated. The Kleene star is the most generic but is accompanied by three additional quantifiers. These quantifiers can be used in the time series patterns. However, the meaning is slightly different. Between two measurements, m and n, an additional, anonymous measurement can be matched if the Kleene star precedes the second measurement pattern: for example, <m>*<n>. The repetition can be limited by a minimum *{a,} – that is, the pattern has to occur at least a times – or by a range *{a,b}, in which case the pattern has to occur at least a times and not more than b times. The last quantifier is +, which is equal to *{1,}.

4.2.4 Time series patterns as temporal properties

Finally, all we have to show is how the time series patterns are linked to node and edge patterns. The same notation as for the static properties is used to link the time series patterns to a graph pattern. To express a temporal property of a node or edge, a time series pattern needs to be added to the node or edge properties, together with the name of the temporal property. This is expressed by writing, after the WHERE keyword, the temporal property key, then an equals sign, followed by a time series pattern. To differentiate the static and temporal properties, both groups are separated by the keyword SERIES, and we will always place the static properties first.

4.2.5 Examples

The following are queries for the running example, given in Example 3.1 and shown in Fig. 1.

Example 4.3. In this example, the query's result is the temperature at 14:00 in a node with the name N6. The corresponding pattern matches the node with name equal to N6 and a water-level property, which is a temporal property, with one measurement pattern x. The timestamp of measurement x needs to be equal to 2022-08-15T14:00.

    MATCH (n:point WHERE name = "N6"
          SERIES water-level = <x>)
    WHERE x.timestamp = "2022-08-15T14:00";

There is only one match in the example graph – that is, node 6 with the value 19 at 14:00.

Example 4.4. In this second example, two different nodes are matched, requiring both to have a temporal property water-level, in which a measurement with the same value at the same time exists.

    MATCH (n:point WHERE SERIES water-level
           = <a>),
          (m:point WHERE SERIES water-level
           = <b>)
    WHERE a.value = b.value
          AND a.timestamp = b.timestamp
          AND NOT n = m;

In the example graph, this query will produce eight matches: one where n maps to node 1 and m maps to node 3 and where the value is 14 at 10:00 and 11:00. There is also one where m is mapped to 5 for 10:00 and 11:00 with a value of 14. There is another one with 𝚗→𝟹 and 𝚖→𝟻 at 10:00 and 11:00 the value 14. The last match is for nodes 2 and 5, with a value of 15 at 12:00 and 13:00.

We remark that there are 16 matches. The same match can be made for each match given with the nodes reversed for n and m. These eight additional matches are not shown. This query can prevent double results by requiring the ID of node n to be smaller than that of node m.

Example 4.5. The following example focuses on variable length paths and the variable-length time series patterns.

    MATCH (n:point WHERE name = "N7" SERIES
           water-level = <a>)
        <-[:path+]-(m:point WHERE SERIES
        water-level = <b>*<c>
    WHERE a.timestamp = "2022-08-15T15:00"
        AND a.timestamp = c.timestamp
        AND b.value >= a.value;

The query should match all nodes upstream of node 7 that contain a temporal property water-level, wherein a measurement exists that occurred before 15:00 and where the value of that measurement is higher than the value in node 7 at 15:00. Valid matches are where m is equal to node 6 and where measurement b is assigned to (14:00,19), (13:00, 18), (11:00, 18), or (10:00, 18). We remark that the measurement of 15:00 in node 6 is not matched because the previous() predicate still needs to be true for measurements b and c. Similarly, node 7 is not matched with n and m because + is used in the edge pattern, which means the edge should occur at least once.

The temporal properties are treated at the same level as static properties, nodes, and edges.² This means the dependency between temporal and static properties can be expressed within one query. The following example depicts a situation where node or edge properties determine the time a temporal property needs to be constrained.

Example 4.6. In this example, the query matches measurements based on values that occurred earlier in the path we want to match. The time that the travel-time series are matched depends on the measurements in the node. Further, down the path, it again depends on the previous matches.³

    MATCH (a:point WHERE SERIES water-level
           =<m1>)
        -[x:path WHERE SERIES travel-time
          =<t1>]->(b:point WHERE SERIES
          water-level=<m2>)
        -[y:path WHERE SERIES travel-time
          =<t2>]->(c:point WHERE SERIES
          water-level=<m3>)
    WHERE t1.value > threshold
        AND t1.time = m1.time
        AND m2.time = m1.time + t1.value
        AND t2.time = m2.time
        AND m3.time = m2.time + t2.value;

Extending this example to include static properties in the constraints is possible. This could be, for example, when only the speed is given, and the length of the edge is needed to calculate the travel time. We want to remark that taking the sum of two values is not described in the logic, nor are other operations on values. We assume they can be used as long as the result is again a valid value. For example, in current Cypher implementations, such operations do exist.

Compared to procedures implemented in a query language or methods implemented using drivers for the databases, the method presented here gives more possibilities for writing constraints. In addition, early pruning of the graph or time series matching is now possible. If they are treated separately, the graph part needs to be retrieved first, and subsequently, the time series need to be queried, or vice versa. This does not provide the same flexibility as our method.

5 Implementation

To demonstrate the idea in practice, we developed a database system that can store graphs as defined in Definition 3.1 and query it with our proposed query language. Based on the additions described in Sect. 4.2, an existing query language is extended to facilitate queries considering the new temporal properties. We chose to realise this with the Neo4j database. It is well-established in practice and provides a good foundation. The open-source query parser from OpenCypher, used in Neo4j, provides a suitable starting place for the query language implementation. Adding other functionalities to Neo4j is possible by using user-defined functions and procedures.

5.1 Storing in practice

There are different options to store the actual time series in the graph database. The storage approach is indifferent of the model presented earlier but usually supports either efficient storage or easier querying. In this work, we use the concept of a full-graph-based approach. That is, to store the time series in the graph database, we use the concept of the full graph model. This means the graph database is used to store the network's topology and time series. The latter are represented as linked lists of nodes in the graph. For each measurement, a node containing the timestamp and value of the measurement is created. These measurements can be linked by edges, connecting all measurements in the temporal order. This means that for each time series, there is a linked list of nodes where each node is a measurement. A head time series node is added to these lists when the time series is linked to a node (of the spatial part). This way, the node of the topology and the head nodes can be linked by a specially typed edge. For edges, this is not possible. There, a similar link can be established by adding a unique ID in the head node of the time series and the static properties of the edge. This would also be possible for nodes, leading to a more consistent design. But we determined that it would impact the query performance, although future research has to verify this. We chose to link the oldest measurement as the first measurement to the head node. This means the latest measurement is stored at the end of the linked list. We selected this approach because, this way, the order of measurements described in the queries corresponds to the order in which they are matched. It could be interesting to store the most recent measurement first because users might be more interested in recent measurements. Of course, the full graph model has a noticeable impact on the total number of nodes and edges stored, as we will show. However, practical experiments have not yet shown any limitations.

5.2 Querying in practice

A new query parser was implemented using Antlr (https://www.antlr.org, last access: 20 November 2024) to implement the query language. This parser can parse the graph query language with time series and translate the queries into standard Cypher. This is possible because time series and measurement patterns are actual graph patterns. Specifically, it is possible to translate each measurement pattern into a node pattern and a time series pattern into a path pattern. These translated patterns can be joined with the pattern for the topology in one query, which can be evaluated by the default query engine of Neo4j. This query translator is implemented with a Spring Boot server that takes a query, sends the translation to the Neo4j database, and returns the result. The user can interact with this system using a web interface implemented using React.

Our grammar for the query language is based on the G4 Cypher grammar. The original grammar specification can be found on the OpenCypher Git repository.⁴ The grammar describes valid measurement and time series patterns by adding the following rules.

We first define the grammar describing a measurement itself. Therefore, a MeasurementPattern is defined and it exists out of the two arrow heads with a variable in between. The following grammar rule already provides the possibility for the implementation to explicitly mention the timestamp or value directly in the measurement patterns in the case of an equality. For example, <2023-10-20,50> equals a measurement on 20 October 2023 and a value of 50.

    oC_MeasurementPattern :
      oC_RangeLiteral?
      oC_LeftArrowHead SP?
      (oC_Variable | (oC_Expression SP?
      ',' SP? oC_Expression))
      SP? oC_RightArrowHead ;

We remark that there is also a range literal that may occur in front of a measurement. This is useful for describing two measurements where one or multiple measurements may occur in between, as we discussed earlier.

The next three elements are all grammar rules we need to describe a series pattern including the name and measurement patterns.

    oC_SeriesPatterns :
      SERIES SP oC_SeriesPattern SP? (','
      SP? oC_SeriesPattern)* ;

    oC_SeriesPattern :
      oC_PropertyKeyName SP? ':' SP?
      oC_MeasurementPattern+ ;

    SERIES :
      ( 'S' | 's' ) ( 'E' | 'e' )
      ( 'R' | 'r' ) ( 'I' | 'i')
      ( 'E' | 'e' ) ( 'S' | 's' ) ;

A series pattern consists of a name for the series followed by a colon and at least one measurement pattern. We introduce a new rule, SeriesPatterns, that allows the user to describe different series patterns separated by a comma. In order to differentiate the temporal properties from the static properties we use the SERIES keyword for which a separate definition rule is used.

To link these series patterns to the existing property patterns, only the rule expressing the mapping for properties needs to be updated to include the time series pattern.

    oC_MapLiteral:
      '{' SP?
      (oC_PropertyKeyName SP? ':' SP?
      oC_Expression SP?
      (',' SP? oC_PropertyKeyName SP? ':'
      SP? oC_Expression SP?)* )?
      (oC_SeriesPatterns)?'}' ;

Compared to the description with GPML, the properties of nodes and edges are not expressed after a WHERE clause but are enclosed in curly brackets. In addition, equals signs linking property keys and property values (for static and temporal properties) are replaced by a colon. This nicely demonstrates that the description of our query language with GPML is easily implemented in any GPML-based query language. We want to remark that, recently, a new specification version was made available, and our changes are not yet compatible with this new version. Our full grammar specification is available on OSF (https://osf.io/j9cn5/, last access: 20 November 2024).

5.3 Experiment

This section focuses on implementing the proposed theory and testing its feasibility. An experiment was conducted to study water quality measurements in the Internet of Water project as a proof of concept. In this section, the tests are designed to determine whether domain experts can express their questions in the newly designed system. A benchmark or performance study is not yet included, but we do report some performance statistics to give some context.

In Flanders, the Internet of Water (IoW) project (https://www.internetofwater.be/wat-is-internet-of-water/, last access: 20 November 2024) aims to enhance monitoring and governance of the Flemish waterways. Hundreds of sensors are deployed and monitored along the Flemish rivers. The sensor data are made available on the data platform of the Flemish environmental agency, which is one of the partners in the project. VITO (Flemish Institute for Technological Research) contributes to the project by analysing the data (Pagán et al., 2020) to answer questions such as the following: what is the salinity at any possible part of the river? What is the current drought status of a river? These questions are important to scientists and managers since climate change leads to more extreme meteorological weather phenomena. These situations affect water supply and water quality, for example, due to the influence of the salty sea on rivers, which can contaminate the drinking water and surrounding land area (Gobin, 2012).

In this set-up, we study the Yser river west of Flanders, depicted in Fig. 2. It is a region prone to salt intrusion because it is close to the sea. In dry periods, salty seawater will push land inwards along the river and intrude via groundwater (Desmet and Bauwel, 2023). For this reason, 42 electrical conductivity (EC) and water temperature (WT) sensors have been placed on the river, and we use the resulting measurements to pose typical questions.

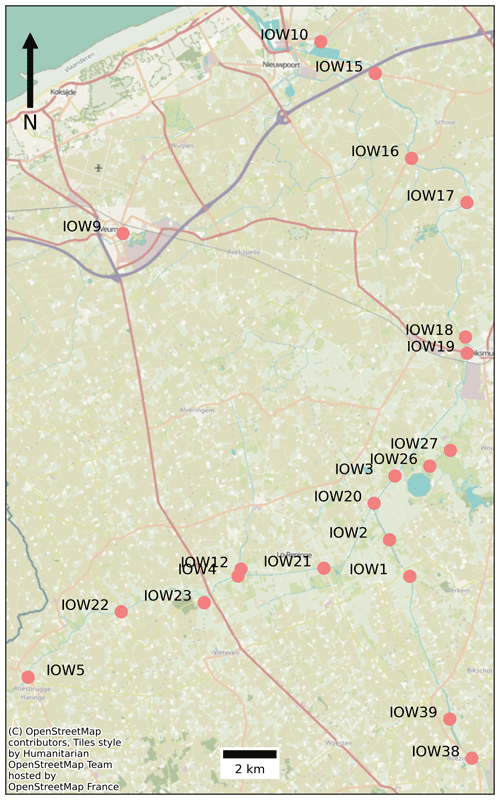
Figure 2 Overview of the Yser river in the west of Belgium. Only a subset of the stations is shown. There are more stations in the data set, but they are not drawn to reduce clutter.

To model the river, we use the Vlaamse Hydrographic Atlas (VHA), a digital GIS data set representing all rivers in Flanders. In this data set, the rivers consist of smaller river segments, represented as line geometries. Sensors are attributed to segments, and because the researchers are interested in studying the river per segment, we chose to model each segment as a node in the graph. If water flows from one segment to another, the two nodes, representing those two segments, are connected by an edge indicating the water flow. In total, there are 534 segments in this use case. The graph thus contains 534 nodes, and they are connected by 541 edges. Distributed over this network are 42 sensors, each producing EC25 measurements every 15 min.⁵ From now on, when values of the measurements are shown, they are in micro-Siemens per centimetre, μS cm⁻¹. We selected the data between 1 January 2022 and 1 May 2022. One time series has 4 months of data with a resolution of 15 min, which results in 11 520 measurements per sensor. However, since it is real life and some measurements are missing, not all series have so many measurements. With the measurements added, the database using the full graph model consists of 395 074 nodes. This results in Neo4j (version 4.2.3) in 53 MB of disk space usage. Details are included in Table 1.

Table 1 Disk usage of the Neo4j database for the Yser data.

Before we discuss the queries in detail, some additional information about the use case is needed. Most of the sensors in the Internet of Water are numbered and named: for example, IOW1 for Internet of Water sensor number 1. Some sensors have slightly different names because they already existed before the project. This name can be used to identify the series of the sensor in the graph uniquely. Our implementation allows users to add labels to the series, as is possible for nodes and edges. For this use case, all series are EC25 measurements, so we assign the label “ec25” to each series. To identify a series by name or label, the following notation is used: name:label:pattern. For example, IOW1:ec25:<a> is the pattern for a series with the name IOW1 and the label ec25. Similarly, we can use the pattern IOW1::<a> for the series with the name IOW1 and no label requirements or :ec25:<a> for a series that has the label ec25 with no name requirements. This addition is not yet described or defined in our proposed logic but is implemented in the proof of concept. We will study the data by posing different questions that researchers within the Internet of Water project pose. These queries will be increasingly complex.

Query 1. Every segment is uniquely identified with the vhas number (the ID of the segment). In this first query, we are going to look up the location of a sensor by querying for the vhas of the segment. The DISTINCT keyword ensures that only one row is returned. Because every measurement in the series can be matched with the pattern, the query without DISTINCT would return as many rows as measurements in the series. The result of this query is one record containing the value 6033646 for n.vhas.

    MATCH (n:segment {SERIES IOW1:ec25:
    <a>}) RETURN DISTINCT n.vhas;

Query 2. The second example query is a typical question where the value of a specific moment and location is requested. In this case, the value of the IOW1 sensor at midnight on 30 March.

    MATCH (n:segment {SERIES IOW1::<a>})
    WHERE a.timestamp = datetime("2022-
    03-30T00:00:00+0000")
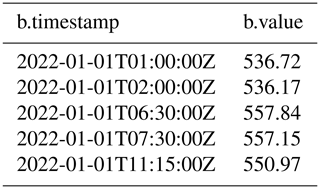
    RETURN a.value;

The value – that is, a.value – is 1230 for the series of IOW1 at the specified timestamp. The result of the query contains only one record because there is only one match in the graph for this pattern.

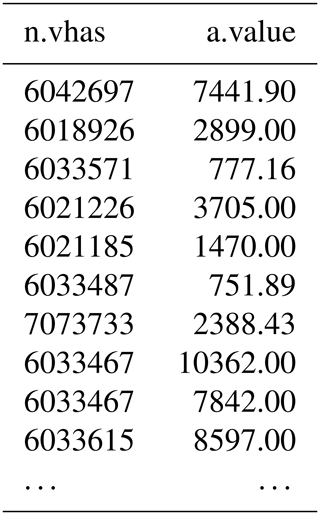
Query 3. With this example, we show how a label can access a series with a specific type. The names or locations might be unknown, but the series type is known. Here, we want to access EC measurements and see their values on 30 March at midnight. The results are shown in Table 2, where, next to the value, the vhas of the segment is returned where the series is on. In total 36 records are returned, but we truncated the table for readability reasons.

    MATCH (n:segment {SERIES :ec25:<a>})
    WHERE a.timestamp = datetime("2022-
    03-30T00:00:00+0000")
    RETURN n.vhas, a.value;

Table 2 Result table containing the first 10 records from the answer to Query 3.

Query 4. This query demonstrates a more advanced series pattern. Because consecutive measurement patterns match consecutive measurements in the series, it is possible to describe a peak. A peak is described as three measurements a, b, and c, where the value of b is higher than the value of a and c.

    MATCH (n:segment {SERIES IOW1:ec25:
     <a><b><c>})
    WHERE a.value < b.value AND c.value
     < b.value
    RETURN DISTINCT b.timestamp, b.value
     LIMIT 5;

The result of this query, where only the first five matches are returned, is shown in Table 3. With each peak, we also return the timestamp of measurement b to see when the peak occurred. Although this query matches many small local peaks, it demonstrates the declarative power of time series patterns. More advanced peak descriptions can be built to find peaks of interest more precisely.

Table 3 Five first records retrieved by Query 4 showing five peak values in sensor IOW1.

Query 5. This query demonstrates how surpassing a threshold in a series can be identified. Such a query interests scientists who, for example, want to find river pollution spills. They know that the EC value would pass a threshold in the event of a spill, but they do not know if and where this happens. The following query matches measurements passing a threshold and returns where and when this occurred.

    MATCH (n:segment {SERIES :ec25:<a>})
    WHERE a.value > 90000
    RETURN n.vhas, a.timestamp, a.value;

The database returns one record: ("6033602", 2022-02-22T11:45Z, 99 999.0). The vhas indicates on which segment in the river the spill would happen, the timestamp of the measurements indicates the time of the event, and we added the measured EC value. This type of query can also be used to set up data validation or find faulty measurements. Likely, this result could be a positive match as a faulty measurement since it is exceptionally high.

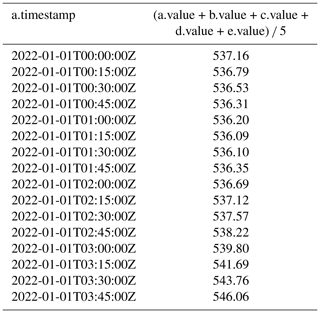
Query 6. The values of the measurements can be used to derive analytical results. In this case, the query retrieves a series at a specific location and calculates a moving average window. Every possible pattern match is returned as a record, and each record selects five consecutive measurements.

    MATCH (n:segment {SERIES IOW1:ec25:
     <a><b><c><d><e>})
    WHERE a.timestamp < datetime("2022-
     01-01T04:00:00+0000")
    RETURN a.timestamp, (a.value+b.value
     +c.value+d.value+e.value)/5;

The results in Table 4 show the moving average for sensor IOW1 during the first 4 h of 01 January.

Table 4 Records showing the average moving window returned by Query 6.

Query 7. Using more advanced graph patterns is useful to describe network structures where the location might be unknown. As this query shows, it looks for a path between two given locations in the network and retrieves the value measured on 30 March at midnight along possible paths. Specifically, the query looks for each ec25-labelled series on a possible path between segment 6031906 and segment 6033656.

    MATCH (:segment {vhas: "6031906"})
           -[:flowsto*]->
          (n:segment {SERIES :ec25:<a>})
           -[:flowsto*]->
          (:segment{vhas: "6033656"})
    WHERE a.timestamp = datetime("2022-
     03-30T00:00:00+0000")
    RETURN n.vhas, a.value;

The database returns the information that at this point in time, there is a path with a series on segment 6042697, and the value there at this point in time is 7441.90.

Query 8. In the IoW project, the water team of VITO established different use cases and models to analyse the Yser river and its water quality. One of the results is the IGOR tool (Desmet and Bauwel, 2023), which is used to analyse electrical conductivity on the Yser river. IGOR provides the ability to interpolate the sensor's measurements for any given location on the river. This interpolation query is the final analysis step to demonstrate and test the database in this context. In the graph, it should be possible to do the same interpolation for any location. Locations in the graphs are considered to be the nodes, and the nodes correspond to segments. This would mean the interpolation can be done for each segment, with or without a sensor. This matches the closest sensor upstream and downstream of the specified location. Subsequently, it interpolates the values for all the provided points in time linearly to the distance between the sensors and the location. This means that, for a given location, the entire time series is interpolated as long as both sensors have a value for the same moment in time.

    MATCH up_path = (up:segment {SERIES
            IOW19:ec25:<x>})-[:flowsto*]
            ->(i:segment {id:"14674"}),
          down_path = (i:segment
            {id:"14674"})-[:flowsto]->
            (down:segment {SERIES
            IMC_910040:ec25:<y>})
    WHERE x.timestamp = y.timestamp
    WITH *, REDUCE(s = 0, seg IN
        nodes(up_path) | s + seg.length)
        as up_distance,
        REDUCE(s = 0, seg IN
        nodes(down_path) | s
        + seg.length) as down_distance
    RETURN  x.timestamp,
        (x.value*(1-(up_distance/
        (up_distance+down_distance))))
        + (y.value*(1-(down_distance/
        (up_distance+down_distance))))

The system's power lies in the fact that the sensors do not need to be known. With an additional subquery, the closest sensors can be determined. The first MATCH part is the subquery that first explores the shortest path to a sensor and calculates the distance to the sensors using two WITH clauses. This step must be separated from the rest because taking the minimum of a group of matches is impossible if other fields are used. Using other fields with aggregation functions results in “group-by” clauses, similar to SQL. To prevent this, the minimum is determined in the subquery. These minimum distances are subsequently used in the second MATCH query to look up the series values and interpolate the EC values. The second part is the same query as before, except that no sensor name is used, and instead, the distance of the matched sensor is compared to the minimum distance obtained in the first part.

    MATCH up_path = (up:segment {SERIES
                    :ec25:<x>})-[:flowsto*]->
                    (i:segment {id: "14674"}),
          down_path = (i)-[:flowsto*]->
          (down:segment {SERIES :ec25:<y>})
    WITH REDUCE(s = 0, seg IN nodes(up_path)
          | s + seg.length) as up_distance,
        REDUCE(s = 0, seg IN nodes(down_path)
          | s + seg.length) as down_distance
    WITH  min(up_distance) as up_min,
          min(down_distance) as down_min

    MATCH up_path = (up:segment {SERIES
                    :ec25:<x>})-[:flowsto*]->
                    (i:segment {id:"14674"}),
          down_path = (i)-[:flowsto*]->
                      (down:segment {SERIES
                      :ec25:<y>}),
    WHERE x.timestamp = y.timestamp
    WITH *,
        REDUCE(s = 0, seg IN nodes(up_path)
         | s + seg.length) as up_distance,
        REDUCE(s = 0, seg IN nodes(down_path)
         | s + seg.length) as down_distance
    WHERE up_distance = up_min AND
         down_distance = down_min
    RETURN i.id, x.timestamp, x.value, y.value,
        (x.value*(1-(up_distance/(up_distance
        +down_distance))))
        + (y.value*(1-(down_distance/
        (up_distance+down_distance))))
        as inter;

For the evaluation, the interpolation is executed for segment 14674 with all values available from 1 until 5 January. The sensor IOW18 is located on this segment, meaning all interpolated values can be compared to actual measured values. The root mean square error can be determined from this, which is 44.61. With values in the range of 450 to 675, this error is less than 10 %. Considering that the sensors have an error margin of up to 10 % for the measured EC values, this result can be considered good. However, the interpolation performance is not the goal of this paper. The main takeaway of this use case is that the proposed system can aid in solving relevant questions for transportation networks. This is what we considered to be proven by being able to fulfil the same work as a dedicated programmed tool such as IGOR.

6 Discussion

We acknowledge that it is possible to use existing temporal graphs to model and query transportation networks. There is work from Kuijpers et al. (2022) that models property graphs with categorical properties through time. Here, we explicitly want to model time series, possibly with a high resolution, and we want to emphasise that the network is stable, whereas the properties can take on many values through time. In addition, our approach exploits the fact that time series have a natural order and uses this in graph pattern expressions. We discussed the advantages of our query language compared to the procedures defined in addition to the existing query language. Nonetheless, procedures might need to be written because not everything is expressible in the proposed query language. That is, expressing constraints on each pair of nodes in a path where the path length is unbounded or expressing constraints on each pair of measurements where the number of measurements is unbounded is impossible.

The usage of labels in the experiment is a useful feature that was possible because the full graph model is used in the implementation. The implementation allows the labels of nodes to be used as labels for the time series. However, this use of labels for time series properties is not fully explored and defined. This should be realised in future steps to standardise the working, independent of the implementation method.

For each topology pattern, multiple measurement patterns can be valid in a time series. The number of matches in the end result is the sum of all valid patterns in the time series for each valid spatial pattern. At most, each measurement is a valid match for a time series pattern, and then the number of topological matches needs to be multiplied by the number of measurements in the relevant time series. This can impact the efficiency. Based on the model and logic presented here, this can now be studied more formally.

At the time of writing, the system is being demonstrated to and evaluated by expert researchers in hydrology and energy fields to evaluate the performance further and identify additional functionality. Therefore, the experiment shown should be seen as a proof of concept. A performance analysis or benchmark is not conducted because the current implementation is not mature enough, and such a study would lead to false results. For example, the current translated queries rely on the transitive closure computation (the “*” operator) in Neo4j. However, earlier research has shown that this operator cannot handle path queries with unbound length as efficiently as other functions (Bollen et al., 2021). However, we would like to indicate the usability based on this proof of concept. The database Neo4j (version 4.2.3) was deployed on a server with Ubuntu 20.04, a two-core system (Intel Xeon Gold 6136 CPU at 3.00 GHz) with 16 GB of memory. Queries 1 to 7 ran and retrieved results between 399 ms and 299 s (299 358 ms), including transferring the records over the network to the local computer. Also, 1 min query times occurred for queries 3, 7, and 8. The translation of the queries from our language to full Cypher was performed between 5 and 382 ms. Again, we want to stress that all these results merely indicate the current state. The implementation is focused on functionality and not performance-oriented, nor are the timings conducted repeatedly. An objective study needs to be conducted to validate the performance of an implementation that exhibits a higher level of technological readiness.

7 Conclusions

Transportation networks are a recurrent research topic and can be modelled using property graphs. With the rise of the Internet of Things, measuring the status of the networks has become easier and the data volume has increased in terms of the number of sensors and resolution of the measurements. These sensors produce time series that, ideally, should be included in the property graphs. Temporal graphs focus on nodes and edges being valid at a certain time. In contrast, transportation networks rarely change their topology, but the measurements are properties of nodes or edges, where the values change through time. Graph databases also exist for storing property graphs, as do time series databases to store the measurements, but a combination, exploiting the characteristics, is missing. In this work, a property graph model with time series is proposed to provide a basic model. This model considers time series on nodes and edges together with the traditional properties as first-class citizens. The model is accompanied by a query language logic, exploiting the natural order in time of the measurements, to describe graph patterns that can be matched. In addition, the paper shows how this logic can be realised in graph query languages based on the Graph Pattern Matching Language (GPML). This all together creates property graphs with time series and leads to a tool set for querying transportation networks or transforming them for more advanced processing. For the first time, it is possible to express patterns where there are constraints that take into account nodes, edges, properties, and measurements of time series – that is, timestamp and value pairs – at the same time. These can all depend on each other, providing the possibility to search and evaluate graphs on all these constraints at the same time. There is more work needed to formally study these graphs with respect to complexity and evaluation, as the increased data size might impact the query evaluation. However, there are also possibilities to exploit optimisations. For example, the new constraints can prune path searches earlier, or path searches can be limit the number of time series that need to be processed. The next step is to realise all this in practice by implementing the property graphs with time series in an actual database and providing the proposed query language together with a query engine that processes the queries. With this theory, a first step is set to store, process, and then also analyse transportation networks based on property graphs with time series. This, in turn, can support research concerned with these networks such as river networks, electricity networks, and heat networks, amongst others.