Feasibility of three-dimensional density tomography using dozens of muon radiographies and filtered back projection for volcanos

This study is the first trial to apply the method of filtered back projection (FBP) to reconstruct three-dimensional (3-D) bulk density images via cosmic-ray muons. We also simulated three-dimensional reconstruction image with dozens of muon radiographies for a volcano using the FBP method and evaluated its practicality.

The FBP method is widely used in X-ray and CT image reconstruction but has not been used in the field of muon radiography. One of the merits of using the FBP method instead of the ordinary inversion method is that it does not require an initial model, while ordinary inversion analysis needs an initial model.

We also added new approximation factors by using data on mountain topography in existing formulas to successfully reduce systematic reconstruction errors. From a volcanic perspective, lidar is commonly used to measure and analyze mountain topography.

We tested the performance and applicability to a model of Omuroyama, a monogenetic scoria cone located in Shizuoka, Japan. As a result, it was revealed that the density difference between the original and reconstructed images depended on the number of observation points and the accidental error caused by muon statistics depended on the multiplication of total effective area and exposure period.

Combining all of the above, we established how to evaluate an observation plan for volcanos using dozens of muon radiographies.

1 Introduction

1.1 Muon radiography and its principles

Muon radiography is a method that can be used to make a map of the inner bulk density structures of large objects such as volcanoes, archeological targets, and so on, using secondary cosmic-ray muons. These muons are generated by the interactions between high-energy primary cosmic rays (the main component is proton) and nuclei in the atmosphere. The flux, energy spectrum, and the zenith angle dependence of secondary cosmic-ray muons have been well researched (e.g., Dorman, 2004; Honda et al., 2004; Patrignani et al., 2016; Nishiyama et al., 2016). Their behavior including energy loss in various materials has also been investigated (Groom et al., 2001). Therefore, when we assume “density length”, which is the integral of multiplication of density and material thickness, we can evaluate the number of penetrating muons. Muon detectors have been developed in the field of particle physics and cosmic-ray physics. To make a bulk density map, we need to measure not only the counts of penetrating muons from the target, but also the direction. For example, nuclear emulsion films (Morishima et al., 2017), hodoscope by scintillating plastic bars (Jourde et al., 2013, Ambrosino et al., 2015), glass resistive plate chambers (Ambrosino et al., 2015), the multi-wire proportional chambers (Oláh et al., 2018) are capable of doing that. By implementing these muon detectors around the target, we can obtain the penetrating muon flux for each direction from the detector; then by comparing to the initial muon flux, we also obtain the attenuation of muons for each directions. By using the topographic data of the target, it is possible to derive the two-dimensional averaged bulk density from the muon attenuation and the path length of the target material.

The principle of X-ray radiography and muon radiography is very similar. There are two significant differences between these two methods: the first is the attenuation length. Typical X-ray beams can penetrate the material in less than 1 m water equivalent. Conversely, some muons can penetrate 1 km of water equivalent because their kinetic energy is very high. The second difference is the origin of the source. The source of cosmic-ray muons is completely environmental and we cannot control the flux while X-ray beams are generated by accelerating the electron artificially. Typically, the number of observed muons is much smaller than in ordinary X-ray radiography.

The first significant result for volcanology was the two-dimensional bulk density imaging of the shallow conduit in Mt. Asama by Tanaka et al. (2007a). Several observations have been made since this research (e.g., Tanaka et al., 2007b, 2014; Lesparre et al., 2012).

1.2 Three-dimensional bulk density imaging

The internal structure of volcanoes gives important information for volcanology. For example, the shape of a shallow conduit affects the eruption dynamics (Ida, 2007). However, muon radiography by only one direction makes just a 2-D image, and this density is the average of material along the muon path direction. Therefore, if we find some contrast in the 2-D density image, we cannot distinguish the actual position of this density anomaly along the muon path direction. To observe the real conduit shape, it is necessary to obtain the density image from different directions to reconstruct the three-dimensional bulk density image.

Tanaka et al. (2010) attempted to observe the target from two directions in Mt. Asama. Nishiyama et al. (2014, 2017) conducted a 3-D density analysis in the Showa-Shinzan lava dome, combined with gravity observation data, which is also sensitive to density. Jourde et al. (2015) evaluated this joint-inversion method between muon radiography and gravity, and they observed and conducted 3-D density analyses by using three-point muon radiography and gravity data (Rosas-Carbajal et al., 2017). These previous studies required prior information on internal density distribution because of insufficient observation data, and they were performed using the inversion technique.

In this study, we propose the application of a 3-D density reconstruction analysis method using filtered back projection (FBP), which does not require prior information. In the FBP method, it is possible to obtain a 3-D density distribution from many projection images only without using the inversion technique (Deans, 2007). This method is applied to X-ray-computed tomography (CT), so it is possible to apply to muon radiography data in principle. However, muon radiography differs from X-ray CT in three points. First, there is a constraint on the number of observation points and position. In X-ray CT, there are hundreds of observation points, and each position is controllable. However, for muon radiography, we can only use several dozen points, and the positions are limited because of topography. Second, the cosmic-ray muon attenuation flux is not a simple exponential. Therefore, the influence of muon statistical error depends on the results of 3-D density, which is not trivial. Third, in the case of muon radiography, typically the amount of signal is much less than for X-ray because the source of cosmic-ray muons is completely environmental. Therefore, it is important to study the features of the FBP method in the case of realistic observations with various numbers of muon radiographies. So we should consider not only the reconstruction error of the FBP method, but also how the error of muon statistics propagates to the final image.

2 Method

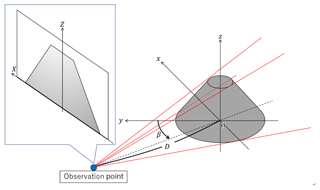
The radon transform is used to obtain projection images from all directions with respect to a density distribution. In muon radiography, this corresponds to acquiring observation data on density length from all directions. For three dimensions, the radon transform $p(X,Z,\mathit{\beta })$ of an object with density $\mathit{\rho }(x,y,z)$ is given by the following:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }p\left(X,Z,\mathit{\beta }\right)=\int \mathit{\rho }\left(-D\sin \mathit{\beta }+{\displaystyle \frac{t}{\sqrt{\mathrm{1}+X^{\mathrm{2}}+Z^{\mathrm{2}}}}}\right.\\ {\displaystyle }& {\displaystyle }\left(X\cos \mathit{\beta }+\sin \mathit{\beta }\right),D\cos \mathit{\beta }+{\displaystyle \frac{t}{\sqrt{\mathrm{1}+X^{\mathrm{2}}+Z^{\mathrm{2}}}}}\\ \text{(1)}& {\displaystyle }& {\displaystyle }\left.\left(X\sin \mathit{\beta }-\cos \mathit{\beta }\right),Z\right)\mathrm{d}t,\end{array}$$

where x, y and z are the positions in a 3-D volume; X and Z are the tangents of azimuth and elevation angle values, respectively; β is the observation point position at a counterclockwise angle with respect to the y axis; and D is the distance between the observation point and the origin. Figure 1 shows the geometric definition for these parameters.

Figure 1 A schematic of radon transform and the definition of parameters x, y, z, X, Z, β and D.

In a 3-D case, if observation data are cone-beam data and observation points only exist on the circumference, a complete inverse radon transform does not exist. Therefore, approximation is needed. Feldkamp (1984) proposed one of the best methods to approximate a solution with a small elevation angle in two dimensions. This approximation is written as follows:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{\rho }\left(x,y,z\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\underset{\mathrm{0}}{\overset{\mathrm{2}\mathit{\pi }}{\int }}\mathrm{d}\mathit{\beta }\underset{-X_M}{\overset{X_M}{\int }}\mathrm{d}X{\displaystyle \frac{D}{L_{\mathrm{2}}^{\mathrm{2}}\sqrt{\mathrm{1}+X^{\mathrm{2}}+Z^{\mathrm{2}}}}}\\ \text{(2)}& {\displaystyle }& {\displaystyle }p\left(X,Z_{\mathrm{0}},\mathit{\beta }\right)h\left(X_{\mathrm{0}}-X\right),\end{array}$$

where $Z_{\mathrm{0}}=z/(D-x\sin \mathit{\beta }-y\cos \mathit{\beta })$, $L_{\mathrm{2}}=\sqrt{\mathrm{1}+Z_{\mathrm{0}}^{\mathrm{2}}}(D+x\sin \mathit{\beta }-y\cos \mathit{\beta })$, $X_{\mathrm{0}}=(x\cos \mathit{\beta }+y\sin \mathit{\beta })/L_{\mathrm{2}}$ and h(X) are a Ram–Lak filter (Ramachandran and Lakshminarayanan, 1971). A feature of this method is that it does not require the shape or initial model of the object. However, when there is a density change in the vertical direction, the accuracy of the approximation decreases. In many examples of volcanic muon radiography, we obtain the shape of the volcano by using other methods; therefore, the influence of changes in the shape can improve the accuracy of the approximation. To estimate the elevation angle, we use the ratio of the path length of the observed muon $q\left(X,Z_{\mathrm{0}},\mathit{\beta }\right)$ to the approximation of $q_h\left(X,Z_{\mathrm{0}},\mathit{\beta }\right)$ (see Fig. 2), which can be written as follows:

$$\begin{array}{}\text{(3)}& {\displaystyle }p{}^{\prime }\left(X,Z,\mathit{\beta }\right)={\displaystyle \frac{q_h\left(X_m,z,{\mathit{\beta }}_n\right)}{q\left(X_m,Z_{\mathrm{0}n},{\mathit{\beta }}_n\right)}}p\left(X,Z,\mathit{\beta }\right),\end{array}$$

where $p{}^{\prime }\left(X,Z,\mathit{\beta }\right)$ is the approximation of the density length for the inverse radon transform. Finally, the reconstruction calculation formula can be written as follows:

$$\begin{array}{ll}\text{(4)}& {\displaystyle }& {\displaystyle }\mathit{\rho }\left(x,y,z\right)=\sum _{n=\mathrm{1}}^N\mathit{\delta }{\mathit{\beta }}_n\sum _{m=\mathrm{1}}^M\mathit{\delta }{X}_m\left(\mathrm{1}-{\displaystyle \frac{X_m}{D\left({\mathit{\beta }}_n\right)}}\mathit{\delta }{D}_n\right){\displaystyle }& {\displaystyle \frac{D\left({\mathit{\beta }}_n\right)}{L_{\mathrm{2}}^{\mathrm{2}}\sqrt{\mathrm{1}+X_m^{\mathrm{2}}}}}{\displaystyle \frac{p\left(X_m,Z_{\mathrm{0}n},{\mathit{\beta }}_n\right)}{q\left(X_m,Z_{\mathrm{0}n},{\mathit{\beta }}_n\right)}}{q}_h\left(X_m,z,{\mathit{\beta }}_n\right)h\left(X_{\mathrm{0}}-X_m\right),\end{array}$$

where m, n is the index of X, β, respectively. We name this the “path length normalization approximation”.

3 Simulation

In this section, we describe the specific components of the simulation calculation. The simulation calculation is divided into the following four steps:

1. parameter setup

2. simulation calculation of the observed muon counts

3. reconstruction calculation using data created in step 2

4. calculations for evaluating the reconstruction results.

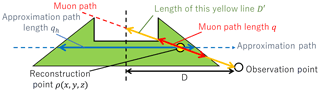
Figure 2 Path length schematic and the approximation difference between the Feldkamp approximation and the path length normalization approximation. In the Feldkamp approximation, the approximation density length is $p{}^{\prime }=D/D{}^{\prime }\times p$. In path length normalization, the approximation density length is $p{}^{\prime }=q_h/q\times p$.

3.1 Parameter setup for target and detector

We simulated and reconstructed the density structure of Omuroyama, which is located in Shizuoka, Japan. We chose this volcano for two reasons. First, this volcano is easily observable from all directions because there are no large structures around the surrounding muon shields in a topographical view. Second, there are no occurrences of muon radiography for these large scoria hills. Omuroyama is a large scoria hill. We base the internal structural model of the large scoria hill on observations at the time of its formation (Luhr and Simkin, 1993). However, there are currently no direct examples of these observations.

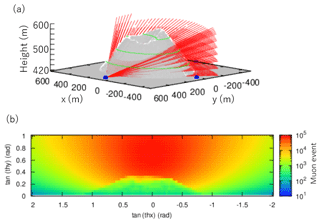
Figure 3 (a) Omuroyama digital elevation model (DEM) data from the Geospatial Information Authority of Japan. (b) The mountain body model and observation points (when the number of observation points is 16). Based on the Omuroyama digital elevation model (DEM) data from the Geospatial Information Authority of Japan. All areas with altitudes of 420 m or less are adjusted to an altitude of 420 m. The resolution is 5 m. The coordinate origin is at the summit (34.903056^∘ N, 139.094444^∘ E). Observation points are located on the circumference with a radius of 500 m centered on a point that was moved x = 50 m and y = 50 m from the summit.

Figure 3 shows the contour map of the Omuroyama model used in the simulation. We assume that the x axis is in the east–west direction, the y axis is in the north–south direction and the origin is the summit.

We configure the internal density distribution similarly to a checkerboard with a side length of 100 m and a density of 1000 and 2000 kg m⁻³. We presume that the first internal density distribution is defined as the original image and is expressed as ${\mathit{\rho }}^{\text{ori}}(x,y,z)$.

The field of view was set from −2 to 2 (−63.4 to 63.4 in degrees) horizontally and 0 to 1 (0 to 45 in degrees) vertically, and the angular resolution was set to 0.04 (2.3 in degrees) in tangent. The observed muon statistics affect the density reconstruction error: the number of muons observed is proportional to the effective area of the device S and the exposure period T. The total effective area and exposure period ST of all muon devices was set as 1000 m² ⋅ days. For example, when the number of observation points is 16, each ST per point is $\mathrm{1000}/\mathrm{16}=\mathrm{62.5}$ m² ⋅ days.

All observation points were assumed to be on the circumference of radius D=500 m placed at the center $\left(x,y\right)=(\mathrm{50}$ m, 50 m) of the mountain. The position of the observation points on the circumference is equal to the rotation angle from the reference line. The position β(rad) of the observation point is defined counterclockwise from the straight line parallel to the y axis and passes through the center $\left(x,y\right)=(\mathrm{50}$ m, 50 m) of the mountain. The value of β, on which the observation point is placed, must always be 1 at β=0, with the rest arranged at equal intervals along the circumference. For example, for the 16-observation-point case, the position of the observation point is ${\mathit{\beta }}_n=\frac{\mathrm{2}\mathit{\pi }}{\mathrm{16}}n$ (n=0, 1,..., 15). Figure 3 also shows the observation point arrangement when there are 16 observation points.

Figure 4 An example of theoretical muon count simulation: (a) the observation state at observation point A; (b) the theoretical muon count observation at that time.

3.2 Simulation calculation of muon count observation

The simulation calculation of the observed number of muons is mainly performed with the following procedures.

1. Calculate the density length $p(X,Z,\mathit{\beta })$ from ${\mathit{\rho }}^{\text{ori}}\left(x,y,z\right)$ for each observation direction viewed from the observation point.

2. Calculate the theoretical muon flux $F_{\mathrm{0}}(X,Z,\mathit{\beta })$ by using a previously prepared relationship among the muon flux, elevation angle and penetration density length. We used the cosmic-ray muon flux model of Honda et al. (2004) and the muon energy attenuation of Groom et al. (2001) for the calculations made here.

3. Calculate the theoretical muon count observation $N_{\mathrm{0}}(X,Z,\mathit{\beta })$ by multiplying $F_{\mathrm{0}}(X,Z,\mathit{\beta })$ the device area S of the observation period T and the solid angle of spatial decomposition in the observation direction.

Figure 4a shows the observation state at observation point A in Fig. 3, and Fig. 4b shows the theoretical muon count observation $N_{\mathrm{0}}(X,Z,{\mathit{\beta }}_{\mathrm{1}})$ at that time.

It is not suitable to use the muon flux table in the region of the 10 m water equivalent or less because of small change. To avoid this region, we did not use these data when the path length $q\left(X,Z_{\mathrm{0}},\mathit{\beta }\right)$ was 10 m or less.

3.3 Reconstruction calculation

The reconstruction calculation procedure is as follows:

1. Calculate the muon flux $F_{\mathrm{0}}(X,Z,\mathit{\beta })$ from the muon number $N_{\mathrm{0}}(X,Z,\mathit{\beta })$, device shape and observation period.

2. Calculate the observed density length $p(X,Z,\mathit{\beta })$ from $F_{\mathrm{0}}(X,Z,\mathit{\beta })$, as well as the relationship among the muon flux, elevation angle and penetration density length.

3. In the path length normalization approximation, calculate path length $q\left(X,Z_{\mathrm{0}},\mathit{\beta }\right)$ and approximation path length

   $q_h\left(X,Z_{\mathrm{0}},\mathit{\beta }\right)$ from the shape information.

4. Calculate the density reconstructed image ${\mathit{\rho }}^{\text{rec}}\left(x,y,z\right)$ from the density length $p(X,Z,\mathit{\beta })$ by using Eq. (4).

4 Simulation results and evaluation

4.1 Systematic error evaluation

We evaluated the systematic error, which is defined as the density difference between the original and reconstructed images at two points. First, we compared the differences between the methods for approximating the elevation angle (i.e., Feldkamp approximation and path length normalization approximation). Second, we quantified the relationship between the observation points and systematic errors.

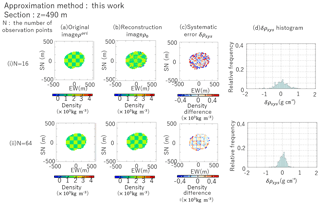
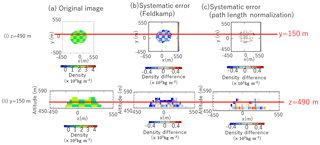
Figure 5 An example of the reconstruction results. All plots were calculated with the results from path length normalized approximation. The altitude of each section is 490 m. Plots are only from the mountains. (a) Original image: ${\mathit{\rho }}^{\text{ori}}(x,y,z)$; (b) reconstruction image: ${\mathit{\rho }}^{\text{rec}}(x,y,z)$; (c) systematic error: $\mathit{\delta }{\mathit{\rho }}^{\text{sys}}(x,y,z)$; (d) δρ^sys histogram: the relative frequency of systematic error. The mean of this plot is μ^sys, and the sample standard deviation is σ^sys.

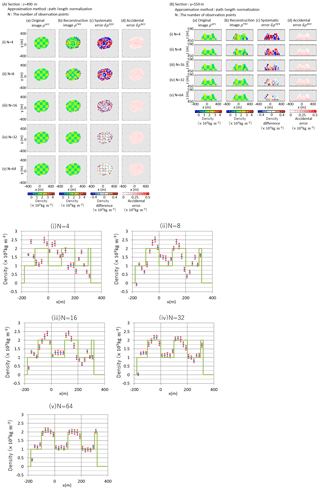
4.1.1 The relationship between the observation points and systematic errors

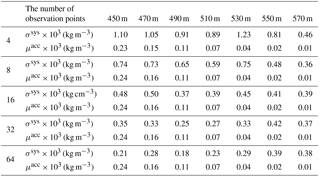
We modeled scenarios with 4, 8, 16, 32, 64, 128 and 256 observation points. The reconstruction results are shown in Fig. 5. The systematic error $\mathit{\delta }{\mathit{\rho }}^{\text{sys}}\left(x,y,z\right)$ was defined as $\mathit{\delta }{\mathit{\rho }}^{\text{sys}}\left(x,y,z\right)={\mathit{\rho }}^{\text{rec}}\left(x,y,z\right)-{\mathit{\rho }}^{\text{ori}}(x,y,z)$. To evaluate the systematic error of all the reconstruction results, we calculated the average of $\mathit{\delta }{\mathit{\rho }}^{\text{sys}}\left(x,y,z\right)$ over the entire object area as the average value of systematic error μ^sys, and the sample standard deviation $\mathit{\delta }{\mathit{\rho }}^{\text{sys}}\left(x,y,z\right)$ was defined as the systematic error distribution σ^sys.

Figure 6 The relationship between the number of observation points and the systematic error deviation σ^sys.

The relationship between the number of observation points and systematic error deviation σ^sys for the entire mountain body is shown in Fig. 6. As the number of observation points increases, the systematic error decreases. At an angular resolution of 0.04, there is almost no change at 64 or more points. At a resolution of 0.02, there is no change with more than 128 points. Therefore, when paying attention to the method of approximating the elevation angle, there are a number of implications when the number of observation points is 64 or more.

Figure 7 A comparison of the Feldkamp approximation and path length normalization approximation.

4.1.2 Comparison of Feldkamp approximation and path length normalization approximation

We simulated both the Feldkamp approximation and path length normalization approximation. Figure 7 shows the reconstruction results of both approximations. In the Feldkamp approximation, the average value of the systematic error μ^sys was $-\mathrm{0.22}\times {\mathrm{10}}^{\mathrm{3}}$ kg m⁻³, whereas it was $-\mathrm{0.01}\times {\mathrm{10}}^{\mathrm{3}}$ kg m⁻³ for the path length normalization approximation.

4.2 Evaluation of accidental errors

We also evaluated the accidental error $\mathit{\delta }{\mathit{\rho }}^{\text{acc}}\left(x,y,z\right)$ in the reconstruction results. This value is the density error caused by the statistical error of muon count $N(X,Z,{\mathit{\beta }}_{\mathrm{1}})$. We assumed that $N_{\mathrm{0}}(X,Z,\mathit{\beta })$ follows a Poisson distribution. We generated 500 types of values with errors assigned, according to the Poisson distribution (in the following, referred to as “muon statistical error”) of $N_{\mathrm{0}}(X,Z,\mathit{\beta })$. This is referred to as muon count with statistical error $N_j^{\text{stat}}(X,Z,\mathit{\beta })$ (j=1 to 500). Here, the index “j” represents the trial of different seeds of random numbers set to $N_j^{\text{stat}}(X,Z,\mathit{\beta })$ for every X,Z and β.

The accidental error $\mathit{\delta }{\mathit{\rho }}^{\text{acc}}\left(x,y,z\right)$ was defined as follows:

$${\displaystyle }\mathit{\delta }{\mathit{\rho }}^{\text{acc}}\left(x,y,z\right)=\sqrt{{\displaystyle \frac{\mathrm{1}}{J-\mathrm{1}}}\sum _{j=\mathrm{1}}^J{\left\{\mathit{\delta }{\mathit{\rho }}_j^{\text{rec}}\left(x,y,z\right)-\mathit{\delta }{\mathit{\rho }}^{\text{rec}}\left(x,y,z\right)\right\}}^{\mathrm{2}}}.$$

Figure 8a, b and c show the spatial distribution of the accidental errors. The accidental error did not depend on the location in the plane. The accidental error was smaller in a section with higher altitude, i.e., a section with a large elevation angle at observation. Moreover, we saw this trend regardless of the number of observation points.

We defined the average of $\mathit{\delta }{\mathit{\rho }}^{\text{acc}}\left(x,y,z\right)$ over the entire object area as the average systematic error value μ^acc, and the sample standard deviation of $\mathit{\delta }{\mathit{\rho }}^{\text{acc}}\left(x,y,z\right)$ was taken as the accidental error distribution σ^acc. Even if the number of observation points increased, no significant changes were observed in the accidental error.

Figure 8 (C). Reconstruction results across z=490 m and y=150 m cross sections. The green lines represent the original image (${\mathit{\rho }}^{\text{ori}}(x,y=\mathrm{150},z=\mathrm{490}))$, the blue points represent the reconstruction results with no accidental errors (${\mathit{\rho }}^{\text{rec}}(x,y=\mathrm{150},z=\mathrm{490}))$ and the red error bar indicates the accidental errors ($\mathit{\delta }{\mathit{\rho }}^{\text{acc}}(x,y=\mathrm{150},z=\mathrm{490}))$.

5 Discussion

5.1 Limit of systematic errors

In Fig. 6, the systematic error does not converge to zero even if the number of observation points increases to more than 200. The observation point position β is represented by a counterclockwise rotation (see Fig. 1 definition of parameters). The interval of β is the angular resolution of the observation point. Increasing the number of observation points is equivalent to increasing the angular resolution of β. When comparing the resolution of X with the resolution of β for the 64-point observation, the resolution of β is $\mathrm{360}/\mathrm{64}=\mathrm{5.6}$^∘, the angular resolution is 2.3^∘ and the resolution of β is lower than X. However, for 256 points, the angular resolution of β is 1.4^∘, which is higher than the angular resolution of X. Figure 6 shows that the systematic error converges near the number of observation points when the resolution of β exceeds the resolution of X. These results indicate that the systematic error depends on the poor resolutions of both X and β.

5.2 Influence of path length on approximation

Why is the average systematic error value different between the Feldkamp approximation and path length normalization approximation? For a volcano with a structure similar to Omuroyama, which is cone shaped with a crater on the summit, the length of the muon path and the elevation angle tend to be shorter than the path length estimated in the horizontal plane (see Fig. 2). In the path length normalization approximation, given that the approximation is made with the path length as a reference, the difference in path length is not important in the Feldkamp approximation; however, the difference in path length is not taken into consideration and is influenced by the change in the path length. As a result, in the Feldkamp approximation, the average value of the systematic error is negative because of the presence of results with short path lengths.

5.3 Elevation angle dependence of accidental errors

Why does the accidental error δρ^acc become smaller as the elevation section increases? The accidental error δρ^acc occurs as a result of muon statistical error. The muon statistical error follows a Poisson distribution. As the number of observed muons increases, the muon statistical error becomes relatively small. Conversely, the muon flux increases as the elevation angle increases. In a section with high altitude, the reconstruction calculation uses both data with a large elevation angle and data with a large number of observed muons, thus reducing the accidental error.

Table 1 The relationship among the number of observation points, systematic error deviation σ^sys (kg m⁻³) and mean accidental error μ^acc (kg m⁻³) on each “z” cross section.

5.4 Relation between muon counts and accidental errors

We performed these simulations under the condition that the total effective area of the observation device is equal. For a 16-point observation, ST per point is 62.5 m² ⋅ days; for a 32-point observation, the device area S per point is 2 times greater at 31.25 m² ⋅ days. Nevertheless, the results for the final accidental error values did not depend on the number of observation points (see Table 1). In Eq. (4), the operator is $\sum _{n=\mathrm{1}}^N$, where N is the number of observation points, and the factor $p_c\left(X_m,Z_{\mathrm{0}n},{\mathit{\beta }}_n\right)$ corresponds to the number of observed muons. p doubles if N is divided by 2 because the effective area also doubles. As a result of the calculation, $\mathit{\rho }\left(x,y,z\right)$ in Eq. (4) remains the same for every x, y and z value (i.e., each voxel). This is why the accidental error is nearly identical between the four-point observation and 64-point observation.

This discussion is able to apply for actual observation with any muon detector type. In the case of an emulsion-type detector, it is easy to divide the effective area S. In the case of hodoscope-type detectors, we can divide the exposure period T by moving the detector to another observation point (e.g., Tanaka, 2016).

5.5 Evaluation of observation plan

We summarized systematic error and accidental error for Omuroyama and ST = 1000 m² ⋅ days in Table 1. We can consider the better conditions of observation from this table. In this table, systematic error is larger than accidental error, excluding the case of 64 points and the 450 m cross section. When the number of observation points is 4 to 32, ST = 1000 m² ⋅ days is sufficient, but in the case of 64 points, it is better to use more STs.

5.6 Limit of this simulation

In this evaluation, the observation points were arranged in a circular orbit. In the future, it is necessary to study more realistic observation point placements. For example, it is difficult to put the observation points on the same plane or in the same interval of β because of topography. We should also work these cases as a next step.

6 Conclusions

We simulated the systematic error of the 3-D density structure of Omuroyama volcano by using several muon detectors via the FBP method with and without information on mountain topography.

• (i)

  Systematic error, which is defined as the density difference between the original and reconstructed images in each voxel internal mountain, depends on the angular resolution of the muon detectors and the number of observation points.

• (ii)

  By comparing the systematic error with and without information on mountain topography, the systematic error deviations are nearly identical. However, the mean value of systematic error becomes more precise in the former case; i.e., the value is more precise when a new method of approximation of path length normalization is used.

In addition, we studied the propagation of muon statistics to the final reconstruction results. By assuming that the multiplication of total effective area and exposure period is fixed and by changing only the number of observation points, the accidental error caused by muon statistics does not change. This accidental error depends only on the total muon statistics for all observation points.

Considering the above, we established how to evaluate an observation plan of dozens of muon radiographies.

7 Future prospects

We assumed that there are tens observation points in this study. The actual observations, which involve many nuclear emulsion muon detectors, were executed by Morishima et al. (2017). Furthermore, Oláh et al. (2018) succeeded in developing a high-quality and inexpensive multi-wire proportional chamber system. Considering such recent advances, the CT volcanic observation of volcanoes by using numerous muon detectors will be possible in the near future.