Soil CO₂ efflux errors are lognormally distributed – implications and guidance

Soil CO₂ efflux is the second-largest carbon flux in terrestrial ecosystems. Its feedback to climate determines model predictions of the land carbon sink, which is crucial to understanding the future of the earth system. For understanding and quantification, however, observations by the most widely applied chamber measurement method need to be aggregated to larger temporal and spatial scales. The aggregation is hampered by random error that is characterized by occasionally large fluxes and variance heterogeneity that is not properly accounted for under the typical assumption of normally distributed fluxes. Therefore, we explored the effect of different distributional assumptions on the aggregated fluxes. We tested the alternative assumption of lognormally distributed random error in observed fluxes by aggregating 1 year of data of four neighboring automatic chambers at a Mediterranean savanna-type site.

With the lognormal assumption, problems with error structure diminished, and more reasonable prediction intervals were obtained. While the differences between distributional assumptions diminished when aggregating data of single chambers to an annual value, differences were important on short timescales and were especially pronounced when aggregating across chambers to plot level.

Hence we recommend as a good practice that researchers report plot-level fluxes with uncertainties based on the lognormal assumption. Model data integration studies should compare predictions and observations of soil CO₂ efflux on a log scale. This study provides methodology and guidance that will improve the analysis of soil CO₂ efflux observations and hence improve understanding of soil carbon cycling and climate feedbacks.

1 Introduction

Instantaneous measurements of soil CO₂ efflux, such as those made with automated respiration chambers, have gained importance for understanding ecosystem carbon dynamics in recent years (Phillips et al., 2016). Poor understanding of the feedbacks of this flux to global change introduces large uncertainties in the predicted terrestrial carbon sink and the projection of the earth system (Friedlingstein et al., 2014). Hence, observations and associated uncertainty estimates at the ecosystem scale have the potential to better resolve model structural uncertainty and predictive ability (Vargas et al., 2010). Among measurement device enclosure types and configuration, chambers represent the most widely used approach for measuring pedon-scale soil CO₂ efflux (Livingston et al., 2006).

Derivation of ecosystem-scale CO₂ efflux, however, involves aggregating data across several chambers and across time. This aggregation poses problems in data analysis. Flux measurements from several chambers, which are typically representative of an area below 1 m², need to be aggregated to the plot level of hectares in order to compare them with ecosystem respiration inferred from eddy-covariance-based net land–atmosphere carbon fluxes (net ecosystem exchange, NEE) (Laville et al., 1999; Christensen et al., 1996; Held et al., 1990; Reth et al., 2005). Problems are indicated by the widespread finding of higher values for aggregated soil CO₂ efflux than NEE (Barba et al., 2018). Theoretically, upscaled soil respiration should always be smaller than ecosystem respiration and NEE, because soil respiration is only a part of ecosystem respiration, and NEE is always smaller than or equal to ecosystem respiration (but also see Janssens et al., 2001).

One challenge is spatial heterogeneity paired with a limited number of measurement locations, which together constrain the precision of the plot-level aggregated flux (Rodeghiero and Cescatti, 2008). Stronger spatial correlations or stronger correlations of soil CO₂ efflux with other more easily measurable spatially distributed variables could help with upscaling. However, the differences between chambers a few meters apart can be as great as between distant chambers (Giasson et al., 2013), and correlation with soil moisture or plant activity is not sufficiently strong and changes across seasons (Leon et al., 2014; Fóti et al., 2016).

A second challenge is posed by a large component of random error. It originates from intrinsic fine-scale process variation such as microbial metabolic pathways, gas diffusion, or microbial population dynamics and, to a smaller extent, from instrumentation error and flux calculations (Lavoie et al., 2015; Pérez-Priego et al., 2015). Random error is usually assumed to be normally distributed with constant variance; however, violation of this assumption poses problems for analysis and aggregation across space and time. A first problem is the increasing variance with increasing flux, which violates the assumption of homoscedasticity of variance, which is the base of many statistical tests. A second problem is the occurrence of strong tails, i.e., higher probability of large absolute errors (Savage et al., 2008; Cueva et al., 2015; Lavoie et al., 2015) compared to the normal assumption. This is often associated with hot spots and hot moments, i.e., locations or times where large fluxes occur on a small scale (Leon et al., 2014; Vargas et al., 2018). To overcome these problems, Savage et al. (2008) proposed using the Laplace distribution. Whether this proposal is applicable depends on how the data will be used. For instance, model data integration studies can use the Laplace assumption by using a cost function that is based on the median absolute deviation rather than the squared difference (Richardson et al., 2006). However, other statistical methods still rely on the normal assumption. For instance, using mixed-effects models (Pinheiro and Bates, 2000; Zuur et al., 2009) in aggregating measurements across several chambers requires the normal assumption for a random effect to represent grouping in the data.

The error distribution model becomes important for studies of model data integration, inverse modeling, and data assimilation (Zobitz et al., 2011; Wutzler and Carvalhais, 2014). In such studies one has to specify a cost function that usually depends on the likelihood of the observations given their uncertainties and the model prediction. The results of such studies often depend strongly on the choice of the cost function (Schoups and Vrugt, 2010; Vrugt and Sadegh, 2013). Using a cost function based on squared differences corresponds to the normal assumption, while a cost function based on the median absolute deviation corresponds to the assumption of error terms following a Laplace distribution (Richardson et al., 2006). A cost function based on the squared difference of log-transformed predictions and observations corresponds to the lognormal assumption.

In this study, we tackle this second challenge of analyzing and aggregating flux data associated with random error. We evaluate the assumption of random error being lognormally distributed as an alternative to the assumption of additive random error from a normal or Laplace distribution.

The lognormal distribution describes measurements with a more or less skewed distribution. It is defined as a continuous probability distribution of a random variable whose logarithm is normally distributed. Such distributions often arise when values are not negative, such as the usual case with soil CO₂ efflux that is mainly driven by autotrophic and heterotrophic respiration (but see Fa et al., 2016, and Roland et al., 2013, for exceptions in alkaline low-organic-matter soils). While the combination of complex additive processes or the sum of random numbers leads to normally distributed observations, a combination of multiplicative processes or the product of random numbers leads to lognormal observations (Limpert et al., 2001) . With the lognormal assumption, log-transforming observations allows further analysis using the normal assumption.

The objectives of this study are, first, to demonstrate that using the lognormal assumption leads to improved analysis of soil CO₂ efflux and, second, to help readers to apply the lognormal assumption to their own data.

Using observed fluxes of four automated soil CO₂ efflux chambers of a Mediterranean tree–grass savanna ecosystem, we compare the results of the lognormal approach to two traditional assumptions of normally or Laplace distributed random error. We show that the lognormal approach diminishes several problems: the lognormal approach leads to more reasonable prediction intervals of aggregated fluxes while keeping continuity of expected values with previously published aggregated fluxes. Finally we discuss assumptions and the implications of our findings.

2 Methods

2.1 Study site and measurement

Data were collected at the ES-LMa FLUXNET site near Majadas de Tiétar, Extremadura, Spain (39^∘56^′25.12^′′ N, 5^∘46^′28.70^′′ W). In May of 2015, 16 semi-automated soil efflux measurement chambers were installed in a stratified random sampling design (Rodeghiero and Cescatti, 2008; Giasson et al., 2013; Phillips et al., 2016) grouped into different treatments and canopy positions. The chambers are an in-house-developed stainless-steel design, connected to a LI-820 (LI-COR, Lincoln, Nebraska, USA) measuring in a half-hourly cycle. During this cycle one chamber at a time would close for a 3 min measurement duration. While there were 16 chambers in all, only data from four chambers in the open grassland stratum within the control plot are used for the purposes of this paper. The aggregate across these four chambers, here, is referred to as the plot-level estimate, although it only represents the open grassland and four chambers are not enough to capture the full spatial variability. Fluxes and their variance were computed from CO₂ concentration time series using the RespChamberProc R package (Sect. 2.8) by estimating the initial slope of concentration increase. These fluxes (plotted in Supplement 1) and associated variance are the input data for this study. They are denoted by R_Si and ${\mathit{\sigma }}_{oi}^{\mathrm{2}}$ in this paper. Data used in this paper range from November 2015 to November 2016. Additional details about the site can be found in El-Madany et al. (2018).

2.2 Distributional assumptions

Each measurement has uncertainty, and this uncertainty can be characterized by a density distribution. For similar environmental conditions, observed fluxes (R_S) scatter around a basic flux (R_B). The noise originates from both instrumentation error (IE) and process variation (PR), a stochastic component intrinsic to the measured soil system. While the nonsystematic component of IE is usually well described as a normally distributed random variable, PR can be described by a normal or Laplace distribution (Eq. 1),

$$\begin{array}{}\text{(1a)}& {\displaystyle }& {\displaystyle }{R}_{\mathrm{S}}=R_{\mathrm{B}}+{\mathit{ϵ}}_{\mathrm{PR},\mathrm{add}}+{\mathit{ϵ}}_{\mathrm{IE}}\text{(1b)}& {\displaystyle }& {\displaystyle }{\mathit{ϵ}}_{\mathrm{PR},\mathrm{add}}\sim \mathrm{norm}(\mathrm{0},{\mathit{\sigma }}_{\mathrm{PR},\mathrm{add}})\mathrm{or}\sim \mathrm{Laplace}(\mathrm{0},b)\text{(1c)}& {\displaystyle }& {\displaystyle }{\mathit{ϵ}}_{\mathrm{IE}}\sim \mathrm{norm}(\mathrm{0},{\mathit{\sigma }}_{\mathrm{IE}}),\end{array}$$

or alternatively with the lognormal distribution Eq. (2):

$$\begin{array}{}\text{(2a)}& {\displaystyle }& {\displaystyle }{R}_{\mathrm{S}}=R_{\mathrm{B}}{\mathit{ϵ}}_{\mathrm{PR},\mathrm{mult}}+{\mathit{ϵ}}_{\mathrm{IE}}\text{(2b)}& {\displaystyle }& {\displaystyle }{\mathit{ϵ}}_{\mathrm{PR},\mathrm{mult}}\sim \mathrm{lognorm}(-{\mathit{\sigma }}_L^{\mathrm{2}}/\mathrm{2},{\mathit{\sigma }}_L^{\mathrm{2}})\text{(2c)}& {\displaystyle }& {\displaystyle }R=\log \left(R_{\mathrm{S}}\right)\approx \log \left(R_{\mathrm{B}}\right)+\log \left({\mathit{ϵ}}_{\mathrm{PR},\mathrm{mult}}\right),\end{array}$$

where ϵ are error terms and σ_PR,add, b, and σ_L are scale parameters of their respective distributions. ϵ_PR,mult is assumed to be lognormally distributed with an expected value of 1. ϵ_IE is usually small compared to R_B ϵ_PR,mult (Lavoie et al., 2015), and hence approximation (Eq. 2c) allows analysis of log-transformed observations. If variance of IE increased with flux magnitude, too, it could also be modeled by a lognormal distribution; however, studies on chamber measurement error did not show such an increasing pattern (Kutzbach et al., 2007, Fig. 8), (Pérez-Priego et al., 2015, Figs. 3 and 4).

Equations (1) and (2c) are extreme cases of a hierarchical model that accounts for both types of error (Appendix B). The lognormal model (Eq. 2c) is sometimes applied without further consideration when log-transforming observations to counteract heteroscedasticity (e.g., Pennington et al., 2020).

2.3 Estimating random error

Error terms are the difference between observed fluxes and a true basic flux. The true flux is unknown but can be estimated by the average flux under similar environmental conditions.

A simple method of estimating the absolute error terms is daily differencing, excluding days with and after rain events (Savage et al., 2008). This daily differencing method (Eq. 3), also called the paired-observation approach, assumes that records 24 h apart represent similar environmental conditions and hence differences in the observed flux (Eq. 3) can be used to estimate the random error. It includes both the non-systematic component of IE and PR (Sect. 2.2).

$$\begin{array}{}\text{(3)}& \mathit{ϵ}=\left(R_{\mathrm{S},t}-R_{\mathrm{S},t+\mathrm{24}}\right)/\sqrt{\mathrm{2}}\end{array}$$

An alternative method is the lookup table approach (LUT). It is commonly used in the marginal distribution sampling method (Reichstein et al., 2005), a method used for filling gaps in data from eddy covariance sensors (Wutzler et al., 2018). When applied to soil CO₂ efflux observations in this study, similar environmental conditions were determined by the hour of the day (±1  h), temperature ($\pm \mathrm{3}{}^{\circ }\mathrm{C}$), soil moisture (±5 %), and a time window. The time window size was increased from ±1 to ±3, 12, and 24 d until there were at least five valid measurements to average across.

A third alternative is modeling the base flux by its relationship with ancillary observations, such as temperature. We tried modeling the CO₂ efflux temperature relationship with varying basal respiration (Gomez-Casanovas et al., 2013; Reichstein et al., 2005). However, cross-validation showed that this approach did not achieve good results for R_S at the Majadas site, because correlation with temperature is generally weak at water-limited sites (Vargas et al., 2018; Rey et al., 2011). Moreover, during dry periods small precipitation events caused respiration pulses without observed concurrent increases in soil moisture at 5 cm soil depth, where soil moisture sensors were located.

When using the lognormal assumption, daily differencing was applied to the log-transformed observed fluxes, whereas for the LUT approach the difference between observed and mean flux was computed with the log-transformed values $\log \left({\mathit{ϵ}}_{\mathrm{PR},\mathrm{mult}}\right)=R-\log \left(R_{\mathrm{S},\mathrm{LUT}}\right)$.

2.4 Estimating correlations in random error

The aggregation across time (Sect. 2.6) must take into account correlations among individual observations, because subsequent measurements are usually autocorrelated.

The correlation cannot be computed by the uncertainties of individual fluxes, ${\mathit{\sigma }}_{oi}^{\mathrm{2}}$, but requires the estimation of individual error terms. After estimating the error terms of all half-hourly fluxes by LUT (Sect. 2.3), we computed the empirical autocorrelation function from the time series of error terms using the acf function implemented in R (Venables and Ripley, 2002). Only the first components of the autocorrelation function can be estimated reliably from the time series. Hence, we only used those components ρ_k before the first negative autocorrelation (Zięba and Ramza, 2011) to construct the variance–covariance matrix. Correlation of error terms farther apart than the maximum number of estimated components of the empirical autocorrelation function was set to 0. Other components were $\mathrm{Cov}({\mathit{ϵ}}_i,{\mathit{ϵ}}_j)={\mathrm{cor}}_{ij}{\mathit{\sigma }}_D^{\mathrm{2}}={\mathit{\rho }}_{|i-j|}{\mathit{\sigma }}_D^{\mathrm{2}}$, where $\mathit{ϵ}={\mathit{ϵ}}_{\mathrm{PR},\mathrm{add}}$ and $\mathit{ϵ}=\log \left({\mathit{ϵ}}_{\mathrm{PR},\mathrm{mult}}\right)$ are the estimated error terms for the normal and lognormal assumption, respectively, and ${\mathit{\sigma }}_D^{\mathrm{2}}$ is the variance across those ϵ.

2.5 Gap filling

Gaps in the flux time series have to be filled before computing the annual aggregated flux. Shorter gaps were filled using the LUT with a window size up to ±24  d (Sect. 2.3). Longer gaps were filled by fitting a random-forest machine learning model (Vargas et al., 2018; Zhao et al., 2020) with predictors “half hour of the day”, global radiation, air temperature, soil temperature, precipitation, vapor pressure deficit (VPD), mean daily soil temperature, mean daily air temperature, soil moisture, mean soil moisture across chambers, and day length. Gap filling extrapolated at maximum 5 d into gaps. The remaining long gaps were treated as missing.

For the plot-level annual aggregation, we estimated the fluxes during long gaps by the mean flux of the other chambers. Using this mean of the other chambers is not fully statistically valid, because one should correct for the chamber offsets that vary slowly across time. However, this was the best estimate we could get for the dataset used.

2.6 Aggregating fluxes with the normal assumption

We are interested in the value and the uncertainty of the flux aggregated across time and across the replicate chambers of the recorded measurement. Across chambers we analyze a sample of four replicates. Across time, we are concerned with the propagation of the random variability induced by the random variations (measurement error and process variation) of the individual measurements (Eq. 4).

$$\begin{array}{}\text{(4)}& \mathrm{Var}\left(\stackrel{\mathrm{‾}}{R_{\mathrm{S}i}}\right)=\mathrm{Var}\left(\stackrel{\mathrm{‾}}{{\mathit{ϵ}}_i}\right)\approx \mathrm{Var}\left({\stackrel{\mathrm{‾}}{\mathit{ϵ}}}_{i\in i_{\mathrm{obs}}}\right)=f({\mathit{\sigma }}_{oi}^{\mathrm{2}},\mathit{\rho })\end{array}$$

The uncertainty of the aggregated value – here, the mean across several soil CO₂ fluxes – is the propagated uncertainty of the uncertainty of the single fluxes, ϵ_i (Eq. 1a). While the mean flux can be computed including gap-filled records, those gap-filled records may introduce systematic errors but should not contribute to the reduction of average random uncertainty with more observations (Eqs. 5b, 9). The uncertainty of error terms is provided by uncertainty, ${\mathit{\sigma }}_{oi}^{\mathrm{2}}$, reported with the observed fluxes, but their autocorrelation, ρ (Sect. 2.4), requires the estimation of error terms.

If IE is dominating, the error is usually well described by independent normal distributions with a mean of 0 (Eq. 1c) with the well-known error propagation rules (Eq. 5).

$$\begin{array}{}\text{(5a)}& {\displaystyle }\begin{array}{rl}E\left[\sum x_i\right]& =\sum E\left[x_i\right]\\ \mathrm{SD}\left[\sum x_i\right]& =\sqrt{\sum \mathrm{SD}(x_i{)}^{\mathrm{2}}},\end{array}\text{(5b)}& {\displaystyle }\begin{array}{rl}E\left[\stackrel{\mathrm{‾}}{x_i}\right]& =\stackrel{\mathrm{‾}}{E\left[x_i\right]}\\ \mathrm{SD}\left(\stackrel{\mathrm{‾}}{x_i}\right)& ={\displaystyle \frac{\mathrm{1}}{\sqrt{n}}}\sqrt{\stackrel{\mathrm{‾}}{\mathrm{SD}(x_i{)}^{\mathrm{2}}}},\end{array}\end{array}$$

where the bar denotes the mean, SD denotes standard deviation, and n is the number of elements in sequence x_i. In our case SD$\left(x_i\right)=\mathrm{SD}\left(R_{Si}\right)=\sqrt{{\mathit{\sigma }}_{oi}^{\mathrm{2}}}$.

However, for time series usually one must consider autocorrelation, where successive measurements are not independent of each other, i.e., where knowing the random error of one measurement holds information for predicting the error of other measurements close in time. One has to add covariance terms when summing variances. For autocorrelated series this leads to formulas dependent on the effective number of observations (Eq. 8) based on the autocorrelation function, which describes how strongly errors are correlated across time lags (Bayley and Hammersley, 1946; Zięba and Ramza, 2011).

$$\begin{array}{}\text{(6)}& {\displaystyle }\mathrm{Var}\left(\stackrel{\mathrm{‾}}{x}\right)={\displaystyle \frac{\mathrm{Var}\left(x\right)}{n_{\mathrm{eff}}}},\text{(7)}& {\displaystyle }\mathrm{Var}\left(x\right)={\displaystyle \frac{n_{\mathrm{eff}}}{n(n_{\mathrm{eff}}-\mathrm{1})}}\sum _{i=\mathrm{1}}^n(x_i-\stackrel{\mathrm{‾}}{x}{)}^{\mathrm{2}},\text{(8)}& {\displaystyle }{n}_{\mathrm{eff}}={\displaystyle \frac{n}{\mathrm{1}+\mathrm{2}{\sum }_{k=\mathrm{1}}^{n-\mathrm{1}}\left(\mathrm{1}-\frac{k}{n}\right){\mathit{\rho }}_k}},\end{array}$$

where $\stackrel{\mathrm{‾}}{x}$ denotes the mean of a vector of random variable x, n is the number of records, and ρ_k denote the coefficients of the autocorrelation function. The autocorrelation function is usually not known, but its first components can be reliably estimated from the data. We followed Zięba and Ramza (2011), who recommend using only the components before the first negative component for k in Eq. (8) instead of all n−1 components (Sect. 2.4).

In the studied case, x is the random error in half-hourly observations with an expected value of 0. One could use the estimated error terms (Sect. 2.3) for (x_i−0), but we used the original observation uncertainty, ${\mathit{\sigma }}_{oi}^{\mathrm{2}}$, given with each observation. Therefore, in Eq. (7) $(x_i-\stackrel{\mathrm{‾}}{x}{)}^{\mathrm{2}}$ is replaced by ${\mathit{\sigma }}_{oi}^{\mathrm{2}}$ and (n_eff−1) is replaced by n_eff because the degree of freedom for computing the mean, x_i, was not used. Then Eq. (6) becomes Eq. (9).

$$\begin{array}{}\text{(9)}& {\displaystyle }\mathrm{Var}\left(\stackrel{\mathrm{‾}}{x}\right){\displaystyle }={\displaystyle \frac{\mathrm{1}}{n_{\mathrm{eff}}}}\stackrel{\mathrm{‾}}{{\mathit{\sigma }}_{oi}^{\mathrm{2}}}\end{array}$$

Hence, the uncertainty ($\sqrt{\mathrm{Var}\left(\stackrel{\mathrm{‾}}{x}\right)}$) declines with $\sqrt{n_{\mathrm{eff}}}$ Eq. (9) compared to $\sqrt{n}$ with uncorrelated random errors of observed fluxes (Eq. 5b). Confidence intervals for aggregated mean fluxes were computed as $\stackrel{\mathrm{‾}}{x}\pm \mathrm{1.96}\mathrm{SD}\left(\stackrel{\mathrm{‾}}{x}\right)$, where SD denotes the standard deviation.

For gap-filled records the residual error is missing. Hence, those records do not contribute to the number of effective observations. However, they are included in computing the mean aggregated flux.

2.7 Aggregating fluxes with the lognormal assumption

An overview of the properties of the lognormal distribution is provided in Appendix A.

For aggregating fluxes across chambers, we first log-transformed each observed flux, R=ln R_S. For the aggregation across replicates, we used the log-transformed values of the same time from different chambers to compute the parameters μ and σ of the distribution (Eq. A4) across chambers. Next, we used the distribution parameters to obtain the expected value (Eq. A2a) and prediction interval between quantiles 2.5 % and 97.5 % (Eq. A6).

For aggregating fluxes of a single chamber across time, we considered the error term in each half-hourly measurement as a realization of a lognormally distributed random variable. The propagation of the error to the sum of such random variables (Eq. A7a) requires the distribution parameters. Hence, these parameters, μ_i and σ_L i, were first computed from the expected value, i.e., the measured flux, R_S i, and its variance that was reported together with the flux, ${\mathit{\sigma }}_{oi}^{\mathrm{2}}$ (Eq. A5). Gap-filled values in the time series complicated the application of Eq. (A7), because they should contribute to the expected value of the sum but should not contribute to the reduction in uncertainty with aggregation across many measurements. Hence, we computed the sum's scale parameter, σ_S, based on original measurements only, but computed the expected value with the inclusion of gap-filled values (Appendix Eq. A2). Hence, the expected value of the sum corresponded to the sum of the gap-filled measured fluxes (Eq. A7a). We provide the R function estimateSumLognormalSample with the lognorm R package (Sect. 2.8) to help with this aggregation.

At observations of low fluxes the instrumentation error component cannot be neglected and the lognormal assumption is violated. Such observations were treated as gap-filled for most of aggregation scenarios; i.e., they contributed to the expected value but not to the error propagation for the mean flux.

2.8 Useful software

For applying these concepts to researchers data, we provide well-documented code in two publicly available packages for the R language.

Computing fluxes from series of concentrations measured inside chambers is provided by the package RespChamberProc (https://doi.org/10.5281/zenodo.3735807), available at GitHub (https://github.com/bgctw/RespChamberProc, last access: 26 May 2020).

Utilities dealing with lognormally distributed data are provided with the package lognorm (https://doi.org/10.5281/zenodo.3735804), available at CRAN (https://cran.r-project.org/web/packages/lognorm/index.html, last access: 26 May 2020). It includes functions for estimating moments and mode, estimating parameters from sample or from summary statistics, and approximating the sum of correlated lognormals.

3 Results

3.1 Distribution and scaling of random errors

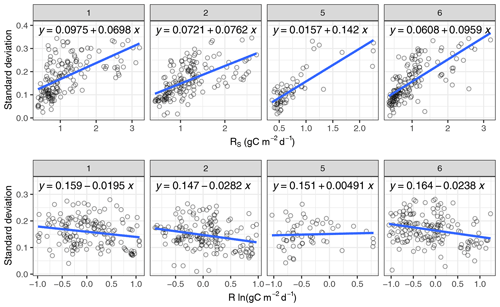
The distribution of error terms obtained by daily differencing had strong tails, while when applying the daily differencing to log-transformed values, R=ln R_S, the distribution of the resulting error became closer to normal than on the original scale (Fig. 1). For large negative outliers the lognormal distribution approximated error distribution even better than the Laplace distribution. Moreover, the log transformation avoided the problematic scaling of random error with flux magnitude. Standard deviation across random error within 1 d scaled with flux magnitude on the original scale (Fig. 2 top) but did not scale on a log-transformed scale (Fig. 2 bottom). Autocorrelation in error terms on a log scale was stronger than autocorrelation in error terms on the original scale (Appendix C).

Figure 1 Quantile–quantile plots compare the sample quantiles of observation error to theoretical distribution quantiles. The closer the points to the displayed 1:1 line, the better the approximation. Both the Laplace distribution with observations on the original scale and the normal distribution with log-transformed observations (lognormal assumption) approximated the sample quantiles better than the normal assumption with observations on the original scale. Here, only data of chamber 2 are shown; the plots of the other chambers look very similar.

Figure 2 On the original scale the error magnitude (standard deviation of error terms across days) scales with flux magnitude (top). Log transformation avoids this problem (bottom). Columns correspond to different chambers.

3.2 Aggregation across replicates

We compared the aggregation of half-hourly fluxes across four neighboring chambers using the lognormal assumption (Sect. 2.7) versus using the normal assumption (Sect. 2.6). For periods without extreme fluxes, the aggregated value and prediction intervals were very similar (Fig. 3). Differences became more evident with high fluxes after rainfall when there was larger variability across chambers. The prediction intervals differed for the following features. First, the upper prediction interval bound was not as strongly influenced by high fluxes; second, the lower bound of the prediction interval was usually close to the lowest observed value. Hence, the lognormal-based lower prediction interval bounds circumvented negative values.

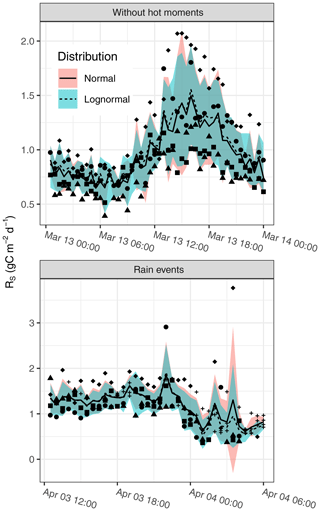
Figure 3 Observed fluxes for neighboring chambers (symbols) and aggregated across chambers: expected values (lines) and 95 % prediction interval bounds (shaded areas). Crosses denote gap-filled values. The lognormal approach avoided negative lower prediction interval bounds with hot moments, for example with rain events on 4 April.

3.3 Temporal aggregation of single chamber fluxes

The expected value of the aggregated fluxes across the 48 half-hourly measurements per day was the same across distributional assumptions. It corresponded to the mean of the observed values. The width of the 95 % prediction interval was similar for most records but differed in a few cases (Fig. 4, top row).

Instances where the lognormal assumption resulted in much wider prediction intervals occurred on days with very low fluxes. In these cases the process variation, which scales with the flux, is small compared to the instrumentation error, and the assumption that error is dominated by the multiplicative component (Eq. 2c) is violated. Those cases need to be treated differently. One way of counteracting the resulting overestimation of uncertainty is setting a gap-filling flag for the uncertainty estimate of very small fluxes (Fig. 4, second row) (Sect. 2.7). This treatment of low fluxes tackles the overestimation of uncertainty for such periods but also leads to slightly wider confidence bounds because now a lower number of observations contribute to the lognormal uncertainty aggregation compared to the normal uncertainty aggregation. The few cases with clearly narrower prediction intervals given the lognormal assumption occurred on days with limited original measurements and large outliers in estimated uncertainty of the single measurements. The lognormal approach was much less sensitive to large outliers and yielded narrower prediction intervals of the aggregated value. When constraining the dataset to days with at least 10 original measurements, most of the differences disappeared (Fig. 4 bottom row).

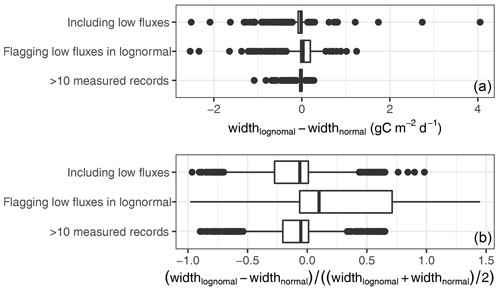
Figure 4 The difference in width of the 95 % prediction intervals for daily aggregates between distributional assumption is shown by box plots on an absolute scale (a) and relative scale (b). Ranges differed only for a few cases as indicated by the outliers dots outside the (degenerate) boxes. Most of these differences were due to very low fluxes or days with few original measurements, and they disappeared when removing problematic observations (see text) as indicated by the box plots in the second and third row.

Contrary to the short-term aggregation, distribution of annually aggregated fluxes of each chamber did not differ much between the two approaches (Fig. 5). The skewness in the distribution of uncertainty of annual estimates almost disappeared, as seen by the similar distance to upper and lower prediction interval bounds in Fig. 5.

3.4 Annual plot-level fluxes

The combined temporal annual and cross-chamber aggregation to the plot level can be done with two alternatives. With one alternative, temporal aggregation (using either the normal or lognormal assumption) is done first, and aggregation across replicates (using the lognormal assumption) estimates is done using the annual estimates of each chamber. With the second alternative, the aggregation across replicates is done first for each half hour across all chambers, and these plot-level fluxes are then aggregated across time. The latter “replicate-first” alternative yielded lower uncertainty estimates (standard deviation of 0.005 instead of 0.02 $\mathrm{gC}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$). The reason is that it neglects any temporally constant or slowly varying component in the location effect. However such a component strongly contributes to the variation across the annual aggregates. This effect is similar to pseudo replicates, as locations did not change between successive measurements.

4 Discussion

4.1 Improvement on distributional problems

With the lognormal assumption the distribution of random error can be inspected on a log scale rather than on the original scale. This improves two distributional problems (Savage et al., 2008). First, the lognormal distribution better approximates the more frequent occurrence of large errors (Fig. 1). Second, the heteroscedastic nature of the random error is reduced; i.e., on a log scale residual variance does not increase with flux magnitude (Fig. 2).

Although the increase of variance could be handled alternatively by an explicit error model in generalized regression or flexible cost functions in model inversion (Schoups and Vrugt, 2010; Toda et al., 2020), the log transformation tackles this problem in a basic way.

The increase of variance with flux magnitude also created the pattern of apparent Laplace distribution (Fig. 1). When we inspected the distribution of subsets of flux errors with similar magnitudes (using LUT, Sect. 2.3), we did not find the Laplace shape. This finding suggests that it is the superposition of normal distributions with different variance at different flux magnitudes that leads to the apparent Laplace shape. This finding is similar to what Lasslop et al. (2008) found for random error of NEE that was measured by eddy covariance. Hence, when the error magnitude is used in model data integration exercises, we argue against using the Laplace assumption and against the associated usage of median absolute deviations (Richardson et al., 2006) when model predictions are compared to single observations. Instead, we recommend using the usual normal-based formula for the cost function but with log-transformed predicted flux and log-transformed observed flux.

4.2 Aggregation across chambers

We assumed that, if a lognormally distributed process variation dominates the observation error of single chambers, then such a process variation also dominates the differences between chambers. Hence, we assumed also a lognormal distribution of measurements across several chambers. With only four replicates, we cannot inspect distributional properties. However, using the lognormal assumption was especially important for periods of high variability across chambers, which occurred at the Majadas de Tiétar site mostly during the dry summer period, similar to findings of Leon et al. (2014). Without using the lognormal assumption, prediction interval bounds of plot-level fluxes would include negative values (Fig. 3).

4.3 Negative fluxes and the lognormal assumption

At the Majadas site, we attribute negative fluxes to measurement error; however, negative fluxes can be real, especially at sandy alkaline soils with low decomposition, i.e., with sparse vegetation. There are abiotic causes for these negative fluxes: carbonate dissolution, soil air shrinkage with temperature and pressure, and CO₂ dissolution in soil water (Fa et al., 2016; Roland et al., 2013). However, the soil at the studied site is not a carbonate soil (inorganic carbon contents of 0.20 to 0.25 gC kg⁻¹ dry soil), and possible abiotic fluxes were magnitudes lower than the observed fluxes at Majadas that are dominated by decomposition of organic material. For examples, in Fig. 3 the confidence bound includes negative fluxes as well fluxes higher than 2.5 $\mathrm{gC}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$.

Nevertheless, the lognormal assumption is not applicable at karstic soils with a high proportion of conditions with real negative fluxes. However, if the proportion of observations with conditions for negative fluxes is low, these conditions can be flagged and the observations can be handled similar to gap-filled records or records where measurement error dominates, which contribute to the expected value but not to the uncertainty estimate.

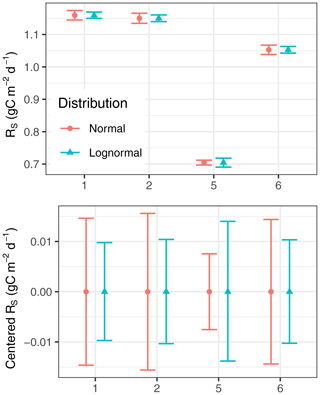
Figure 5 Annually aggregated mean flux estimates (symbols) and their 95 % prediction interval bounds (bars) are of similar width for normal and lognormal assumption. The x axis denotes different chamber locations. The aggregation excluded long gaps, which led to different aggregation periods and differences across chambers.

4.4 Daily temporal aggregation

Further, we explored consequences of aggregating measurements of a single chamber across time using the lognormal assumption compared to classical aggregation using the normal assumption. A single chamber measurement representing a time period can be assumed to be a normal or a lognormal random variable. These assumptions resulted in different aggregated uncertainties when aggregating across a few days (Fig. 4). We argue that the choice of distributional assumptions depends on the sampling interval, the magnitude of measurement error, and the autocorrelation length of the process variation. If measurements are frequent relative to process autocorrelation length, the uncertainty is dominated by the instrumentation error (from the measurement device), which can be assumed to follow a normal distribution. Alternatively, if a single measurement represents a longer period, the uncertainty will be dominated by process variation. While process variation dominates random error at a daily measurement resolution (Lavoie et al., 2015), we cannot distinguish between those two cases from our series of half-hourly measurements.

However, we encountered a problem when fluxes were very low, where the instrumentation error component becomes dominant and the lognormal assumption is violated. If the lognormal assumption is applied to such cases, time aggregation leads to overestimation of uncertainty, because it overestimates the multiplicative error. Those records need to be flagged similar to gap-filled records before aggregation using the lognormal approach (Sect. 2.7).

4.5 Annual temporal aggregation

When half-hourly measurements of a single chamber were aggregated to longer timescales such as to annual aggregates, the differences in uncertainty bounds between distributional assumptions decreased (Fig. 5). There was a tendency towards slightly narrower bounds with the lognormal assumptions. We argue that this is due to the lognormal approach being more robust to the influence of few large values. For chamber 5 the lognormal-based uncertainty is wider, because there were long gaps during the season of large fluxes, and hence there was a relatively larger proportion (15 %) of low fluxes that were excluded from error propagation where the assumption of dominating process variance was violated. Moreover, the autocorrelation structure in error terms was not detected properly on the original scale for this chamber (Appendix C).

Also the skewness disappeared (Fig. 5). This was a consequence of relative uncertainty decreasing with the number of aggregated measurements, which led to less skew and to lognormal distributions which are close to normal (Fig. A1). This is also in line with the general idea of the central limit theorem (Lindeberg, 1922), although we could not find a version of the theorem that matches the combined non-iid and non-Gaussian case of single terms for the time series of this study.

Overall, we suggest using the lognormal assumption for aggregating across fluxes from replicated chambers but the normal assumption for aggregating half-hourly observations of a single chamber across time with number of records exceeding, say, 40.

When deciding whether to first aggregate across chambers or across time, the “cross-chamber-first” alternative (Sect. 3.4) wrongly assumes that the cross-chamber aggregated values are only correlated in time. They are, however, measured at the same spatial locations and fully correlated in space. Therefore, whenever measurement locations are fixed and a plot-level estimate is required, the cross-chamber aggregation should be computed as the last step.

4.6 Process variation

Our finding on the suitability of the model of a multiplicative, lognormal process variation sheds new light on the process variation, i.e., the as-yet-unattributed soil processes that generate random fluctuations in soil CO₂ efflux observations. Lavoie et al. (2015) proposed two mechanisms for process variation. First, a higher diversity of active metabolic pathways associated with a wider range of pore-scale respiration rates at high temperature could result in larger variability of fluxes. Because higher temperatures are associated with higher fluxes, this would explain the increase of variance with flux magnitude. Second, gas diffusion rates might increase due to heat produced during respiration. Similarly, gas transport processes in soil can change with pore space varying with soil moisture (Maier et al., 2011).

We propose the alternative hypothesis based on small-scale spatial heterogeneity and stochasticity of the temperature sensitivity of chemical reactions involved. Metabolic rates associated with microbial communities differ across micrometer distances in their temperature sensitivity, and these metabolic rates in turn largely drive respiration and soil CO₂ efflux. Respiration is related to such temperature sensitivity in an exponential manner (Lloyd and Taylor, 1994). Hence, if variation in temperature sensitivity is normally distributed, then the log of respiration is normally distributed; i.e., variation in respiration is lognormally distributed. This argument is transferable to process variation distribution of fluxes on the leaf and ecosystem scale.

4.7 Recommendation checklist

To obtain plot-level estimates of soil CO₂ efflux, one typically has to aggregate time series of several chambers. For such cases we recommend the following procedure based on the experience gained with this study.

• Estimate error terms by daily differencing or, preferentially, LUT.

• Fill gaps in the data and flag gap-filled records.

• Flag low-flux conditions where instrumentation error is dominating or where real negative fluxes can occur.

• Aggregate data of single chambers across time. For confidence or prediction intervals, take care of autocorrelation. Use the lognormal assumption if the aggregation runs over a limited number of observations, less than 40, say. Take care of flagged values that should contribute to the estimated flux but should not contribute to the flux uncertainty (Sects. 2.7 and 4.4).

• For plot-level estimates aggregate the time-aggregated estimates across several chambers using the lognormal assumption, as the last step.

In model data integration compare predictions and observations of soil CO₂ efflux on a log scale.

5 Conclusions

The presented methodology and tools will help researchers to better analyze soil CO₂ efflux measurements using different assumptions. The lognormal assumption improves two error distribution problems: first, the heteroscedasticity, i.e., the increase of error terms variance with flux magnitude, and, second, the strong upper tail. Hence, model data integration studies should consider comparing model predictions and observations on a log-transformed scale. For annual aggregation of high-frequency flux measurements of a single chamber the normal assumption is plausible and the difference in estimated uncertainty between assumptions is small. We argue that the lognormal assumption is probably more suitable than the normal assumption when aggregating over replicated chambers, although we studied only four replicates. Researchers are encouraged to compute and report the parameters of the lognormal distribution. Whenever plot-level estimates are required, cross-chamber aggregation should be performed as the last step after temporal aggregation. The lognormal assumption provides a new perspective on the as-yet-unattributed processes responsible for process variation in fluxes. It implies that these processes operate in a multiplicative rather than in an additive way. The presented argument of respiration being exponentially related to a fluctuating temperature sensitivity is also true for leaf and ecosystem fluxes. Hence we suggest testing whether or not the variability of error terms of such fluxes is better described by a lognormal distribution.

Appendix A: The lognormal distribution

This section compiles the properties of the lognormal distribution that are most relevant to using the lognormal assumption when aggregating observations.

A1 Distribution, parameters, and statistics

The density of the lognormal distribution is described by two parameters (Eq. A1).

$$\begin{array}{}\text{(A1)}& f\left(x\right)={\displaystyle \frac{\mathrm{1}}{x}}\cdot {\displaystyle \frac{\mathrm{1}}{\mathit{\sigma }\sqrt{\mathrm{2}\mathit{\pi }}}}\exp \left(-{\displaystyle \frac{(\ln x-\mathit{\mu }{)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}}\right)\end{array}$$

Traditionally, parameters are given on a log scale, where the location parameter μ describes the magnitude of a random variable and the parameter σ describes the spread. Their exponentials ${\mathit{\mu }}^{*}=e^{\mathit{\mu }}$ and ${\mathit{\sigma }}^{*}=e^{\mathit{\sigma }}$ describe the distribution on the original scale, with μ^* corresponding to the median and σ^* being the the multiplicative standard deviation. The interval $\left({\mathit{\mu }}^{*}/{\mathit{\sigma }}^{*\mathrm{2}},{\mathit{\mu }}^{*}{\mathit{\sigma }}^{*\mathrm{2}}\right)$ denoted by ${\mathit{\mu }}^{*}{}^{\times }/{\mathit{\sigma }}^{*\mathrm{2}}$ contains about 95.5 % of the probability mass.

The first two moments, i.e., the expected value and the variance, are given by Eq. (A2). The expected value is larger than the median, μ^*, because the distribution is skewed to the left. With decreasing σ^* the skewness decreases and the shape of the distribution gets closer to normal (Fig. A1).

$$\begin{array}{}\text{(A2a)}& E\left[X\right]=\stackrel{\mathrm{‾}}{x}=\exp \left(\mathit{\mu }+{\displaystyle \frac{{\mathit{\sigma }}^{\mathrm{2}}}{\mathrm{2}}}\right)={\mathit{\mu }}^{*}{e}^{{\mathit{\sigma }}^{\mathrm{2}}/\mathrm{2}}\end{array}$$

$$\begin{array}{}\text{(A2b)}& \begin{array}{rl}\mathrm{Var}\left(X\right)& ={\mathit{\sigma }}_o^{\mathrm{2}}=\left[\exp \left({\mathit{\sigma }}^{\mathrm{2}}\right)-\mathrm{1}\right]\exp \left(\mathrm{2}\mathit{\mu }+{\mathit{\sigma }}^{\mathrm{2}}\right)\\ & =\left(e^{\left({\mathit{\sigma }}^{\mathrm{2}}\right)}-\mathrm{1}\right){\stackrel{\mathrm{‾}}{x}}^{\mathrm{2}}\end{array}\end{array}$$

Equation (A2b) relates the standard deviation to the relative error, i.e., the coefficient of variation: $\mathrm{cv}={\mathit{\sigma }}_o/\stackrel{\mathrm{‾}}{x}$ (Eq. A3). A relative error of 5 % corresponds to ${\mathit{\sigma }}^{*}=\mathrm{1.05}$, and approximating the lognormal distribution by a normal distribution worked reasonably well up to ${\mathit{\sigma }}^{*}=\mathrm{1.2}$ (Fig. A1), corresponding to a relative error of 18 %.

$$\begin{array}{}\text{(A3a)}& {\displaystyle }& {\displaystyle }\mathrm{cv}=\sqrt{e^{\left({\mathit{\sigma }}^{\mathrm{2}}\right)}-\mathrm{1}}\text{(A3b)}& {\displaystyle }& {\displaystyle }\mathit{\sigma }=\sqrt{\ln ({\mathrm{cv}}^{\mathrm{2}}+\mathrm{1})}\end{array}$$

The parameters of the distribution can be estimated by the log-transformed sample (Eq. A4).

$$\begin{array}{}\text{(A4a)}& {\displaystyle }& {\displaystyle }\widehat{\mathit{\mu }}=\mathrm{mean}\left(\ln x\right),\text{(A4b)}& {\displaystyle }& {\displaystyle }\widehat{\mathit{\sigma }}=\mathrm{SD}\left(\ln x\right),\end{array}$$

where $\mathrm{mean}\left(x\right)=\stackrel{\mathrm{‾}}{x}$ and SD(x) denote the sample mean and standard deviation, respectively. Alternatively, the distribution parameters can also be estimated from the mean and standard deviation on the original scale, σ_o, by Eq. (A5) (Limpert et al., 2001).

$$\begin{array}{}\text{(A5a)}& {\displaystyle }& {\displaystyle }\widehat{\mathit{\mu }}=\log \left(\stackrel{\mathrm{‾}}{x}/\sqrt{\mathit{\omega }}\right),\text{(A5b)}& {\displaystyle }& {\displaystyle }\widehat{\mathit{\sigma }}=\sqrt{\ln \left(\mathit{\omega }\right)},\end{array}$$

where

$$\begin{array}{}\text{(A5c)}& {\displaystyle }& {\displaystyle }\mathit{\omega }=\mathrm{1}+{\mathrm{cv}}^{\mathrm{2}}\mathrm{and}\text{(A5d)}& {\displaystyle }& {\displaystyle }\mathrm{cv}={\mathit{\sigma }}_o/\stackrel{\mathrm{‾}}{x}\text{is the coefficient of variation. }\end{array}$$

The quantiles of the lognormal distribution are derived from the quantiles of the normal distribution (Eq. A6).

$$\begin{array}{}\text{(A6)}& q_{\mathrm{lognormal}}(p;\mathit{\mu },\mathit{\sigma })=e^{q_{\mathrm{normal}}(p;\mathit{\mu },\mathit{\sigma })}\end{array}$$

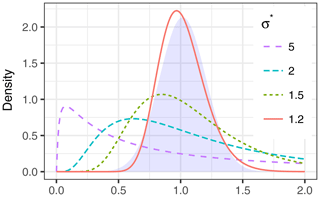
Figure A1 Density distributions of lognormal distributions (lines) get closer to normal density (shaded area) as multiplicative standard deviation σ^* decreases down to 1.2 for the same ${\mathit{\mu }}^{*}=\mathrm{1}$.

For example, the 97.5 % quantile of the standard normal distribution with $q_{\mathrm{normal}}(\mathrm{97.5},\mathrm{0},\mathrm{1})\approx \mathrm{1.96}$ directly translates to the lognormal, $q_{\mathrm{lognormal}}(\mathrm{97.5},\mathrm{0},\mathrm{1})\approx e^{\mathrm{1.96}}$. Hence, a 95 % confidence interval of the normal is within μ±1.96σ and that of the lognormal is within e^μ±1.96σ, also denoted ${\mathit{\mu }}^{*}{}^{\times }/({\mathit{\sigma }}^{*}{)}^{\mathrm{1.96}}$. Note that this confidence interval is not symmetrical, with the upper bound being further away from the median.

The product of several lognormal random variables is again lognormally distributed, because the sum of normally distributed random variables on a log scale is again normally distributed.

A2 Sum of lognormal random variables

For the sum of several lognormal random variables, to date, there is no closed formula known. However, it can be approximated by a lognormal distribution, and the parameters of this distribution can be found by various methods (Fenton, 1960; Cobb et al., 2012; Lo, 2013; Messica and Messica, 2016; Furman et al., 2020). In this study we use the approximation by Lo (2013), which can be applied to the sum of correlated random variables (Eq. A7).

$$\begin{array}{}\text{(A7a)}& S_{+}=E\left[\sum _i{X}_i\right]=\sum _{i}E\left[X_i\right]=\sum _i{e}^{{\mathit{\mu }}_i+{\mathit{\sigma }}_i^{\mathrm{2}}/\mathrm{2}},\end{array}$$

$$\begin{array}{}\text{(A7b)}& \begin{array}{rl}{\mathit{\sigma }}_{\mathrm{S}}& =\mathrm{1}/S_{+}^{\mathrm{2}}\sum _{i,j}{\mathrm{cor}}_{ij}{\mathit{\sigma }}_i{\mathit{\sigma }}_j{e}^{{\mathit{\mu }}_i}{e}^{{\mathit{\mu }}_j}\\ & =\mathrm{1}/S_{+}^{\mathrm{2}}\sum _{i,j}{\mathrm{cor}}_{ij}{\mathit{\sigma }}_i{\mathit{\sigma }}_{j}E\left[X_i\right]e^{-{\mathit{\sigma }}_i^{\mathrm{2}}/\mathrm{2}}E\left[X_j\right]e^{-{\mathit{\sigma }}_j^{\mathrm{2}}/\mathrm{2}},\end{array}\end{array}$$

$$\begin{array}{}\text{(A7c)}& {\mathit{\mu }}_{\mathrm{S}}=\ln \left(S_{+}\right)-{\mathit{\sigma }}_{\mathrm{S}}^{\mathrm{2}}/\mathrm{2},\end{array}$$

where S₊ is the expected value of the sum, i.e., the sum of the expected values of the terms. μ_S and σ_S are lognormal distribution parameters of the sum, μ_i and σ_i are the lognormal distribution parameters of the added random variables, and cor_ij is the correlation between two added random variables on a log scale, which for time is computed from estimated autocorrelation ρ_k (Sect. 2.4).

There might be flagged terms that should contribute to the sum but should not contribute to the reduction of relative uncertainty with error propagation across many terms. Examples are gap-filled values or observations where a proper estimate of the multiplicative uncertainty is missing. In this case, S₊ and σ_S are first computed using only the non-flagged terms. Next S₊ and μ_S are recomputed using all terms. Hence, the expected value of the sum equals the sum of expected values of the terms. The first computation of S₊ based on the non-flagged terms is lower, and hence the estimate of uncertainty, σ_S, is higher than the computation using all terms.

The multiplicative standard deviation, σ^*, is invariant to multiplications of the random variable. Hence, it is the same for the mean as for the sum of several lognormally distributed random variables. For the mean only the scale parameter changes compared to the sum as ${\mathit{\mu }}_{\mathrm{mean}}^{*}={\mathit{\mu }}_{\mathrm{S}}^{*}/n$ or ${\mathit{\mu }}_{\mathrm{mean}}={\mathit{\mu }}_{\mathrm{S}}-\ln \left(n\right)$, where n is the number of aggregated variables.

Appendix B: Latent Gaussian model formulation

The observations of CO₂ efflux of a single chamber can be formulated as a latent Gaussian model (LGM), a subset of Bayesian hierarchical models (Rue et al., 2009).

$$\begin{array}{}\text{(B1a)}& {\displaystyle }& {\displaystyle }{R}_{\mathrm{S}}=R_{\mathit{\mu }}+{\mathit{ϵ}}_{\mathrm{IE}},\text{(B1b)}& {\displaystyle }& {\displaystyle }\ln \left(R_{\mathit{\mu }}\right)=R_{\mathrm{B}}+{\mathit{ϵ}}_{\mathrm{PR}},\text{(B1c)}& {\displaystyle }& {\displaystyle }{\mathit{ϵ}}_{\mathrm{IE}}\sim N(\mathrm{0},{\mathit{\sigma }}_{\mathrm{IE}}),\text{(B1d)}& {\displaystyle }& {\displaystyle }{\mathit{ϵ}}_{\mathrm{PR}}\sim N(\mathrm{0},\mathit{\sigma }),\text{(B1e)}& {\displaystyle }& {\displaystyle }\ln \left({\mathit{\sigma }}_{\mathrm{IE}}^{-\mathrm{2}}\right)\sim \mathrm{Gamma}(a_{\mathrm{IE}},b_{\mathrm{IE}}),\text{(B1f)}& {\displaystyle }& {\displaystyle }\ln ({\mathit{\sigma }}^{-\mathrm{2})}\sim \mathrm{Gamma}(a,b),\end{array}$$

where ϵ are normally distributed error terms with shape parameter σ. Their corresponding precisions 1∕σ² are distributed by a log-Gamma hyperprior with specified parameters. R_b is the true value of log (soil CO₂ efflux). It can be plugged in by the LUT approach, modeled as a linear model of covariates, or estimated together with the σ parameters given a proper constraint on their covariances in time and/or space of environmental variables.

Such a LGM can be estimated using INLA (Rue et al., 2009) (Appendix Eq. B3) or Markov chain Monte Carlo sampling (Metropolis et al., 1953; Gelman et al., 1995; Zobitz et al., 2011).

Instrumentation error is of magnitude IE=σ_IE, and process variation on the original scale is of magnitude $\mathrm{PR}=R_{\mathrm{B}}(e^{\mathit{\sigma }}-\mathrm{1})$. This study deals with two special cases. Since the lognormally distributed process variation scales with the flux magnitude, we expect it to dominate at large fluxes, while we expect the instrumentation error to dominate at low fluxes.

B1  PR≪IE

If the lognormally distributed variation is small compared to the normally distributed one, it can be neglected. The model then simplifies to Eq. (B2).

$$\begin{array}{}\text{(B2a)}& {\displaystyle }& {\displaystyle }{R}_{\mathrm{S}}=R_{Be}+{\mathit{ϵ}}_{\mathrm{IE}},\text{(B2b)}& {\displaystyle }& {\displaystyle }{\mathit{ϵ}}_{\mathrm{IE}}\sim N(\mathrm{0},{\mathit{\sigma }}_{\mathrm{IE}}),\text{(B2c)}& {\displaystyle }& {\displaystyle }\ln \left({\mathit{\sigma }}_{\mathrm{IE}}^{-\mathrm{2}}\right)\sim \mathrm{Gamma}(a_{\mathrm{IE}},b_{\mathrm{IE}}),\end{array}$$

with $R_{\mathrm{Be}}=e^{R_{\mathrm{B}}}$. When assuming a flat prior ($a_{\mathrm{IE}}=-\mathrm{1}$; b_IE=0), this model corresponds to a classical linear regression, i.e., the normal assumption.

B2  IE≪PR

If the normally distributed variation is small compared to the lognormally distributed one, it can be neglected. The model then simplifies to Eq. (B3).

$$\begin{array}{}\text{(B3a)}& {\displaystyle }& {\displaystyle }\log \left(R_{\mathrm{S}}\right)=R_{\mathrm{B}}+{\mathit{ϵ}}_{\mathrm{PR}}\text{(B3b)}& {\displaystyle }& {\displaystyle }{\mathit{ϵ}}_{\mathrm{PR}}\sim N(\mathrm{0},\mathit{\sigma })\text{(B3c)}& {\displaystyle }& {\displaystyle }\ln \left({\mathit{\sigma }}^{-\mathrm{2}}\right)\sim \mathrm{Gamma}(a,b)\end{array}$$

When assuming a flat prior ($a=-\mathrm{1}$; b=0), this model corresponds to a classical linear regression of the log-transformed values, i.e., the lognormal assumption.

B3 Fitting the LGM using INLA

During periods with similar environmental conditions, we can model R_B as a smooth function with time and fit it together with the magnitudes of the two error types, σ_IE and σ, without the need for gap filling before.

We fitted model Eq. (B1) to the data of chamber 2 for a 5 d period in April using INLA (Rue et al., 2009) and its default priors and compared the posterior estimates of the two standard deviations. While the standard deviations were both significant and of the same magnitude (σ_IE: $\mathrm{mean}=\mathrm{0.047};q\mathrm{025}=\mathrm{0.021};q\mathrm{975}=\mathrm{0.088})$, the transformation of the lognormal error to the original scale indicated the deviations due to the lognormal error had a larger effect (R_B(e^σ−1): $\mathrm{mean}=\mathrm{0.095};q\mathrm{025}=\mathrm{0.024};q\mathrm{975}=\mathrm{0.18})$.

During shorter (∼ weeks) periods, we can assume that the difference between chambers can be modeled as a random intercept slope in the linear predictor on a log scale, which allows fitting data of all chambers together. A simpler random-intercept-only model still showed patterns in the residuals.

Compared to the single-chamber fit, the estimate of the normal error decreased further (σ_IE=0.010), whereas the estimate of the lognormal error increased ($R_{\mathrm{B}}(e^{\mathit{\sigma }}-\mathrm{1})=\mathrm{0.27}$), and standard deviation of chambers intercept was larger ($R_{\mathrm{B}}(e^{{\mathit{\sigma }}_{\mathrm{Ch}}}-\mathrm{1})$: $\mathrm{mean}=\mathrm{1.0};q\mathrm{025}=\mathrm{0.55};q\mathrm{975}=\mathrm{1.9}$).

This indicates that assumption of negligible instrumentation error compared to the lognormally distributed process variation (IE≪PR) is viable.

In addition to the model with both error terms, we fitted models with only one of the error terms included and compared models by the deviance information criterion (DIC) (Spiegelhalter et al., 2002). The lower DIC of the full model of −5130 indicated a better fit compared to the lognormal-error-only model with DIC of −1080, which was again better than the normal-error-only model with a DIC of 555.

As an outlook, we will study if this approach can be extended to longer periods and adapted to more complex models with time-varying differences between chambers.

Appendix C: Autocorrelation in error terms

Autocorrelation between error terms is important for propagation of the uncertainty when aggregating over time (Sect. 2.6).

The coefficients of the empirical autocorrelation function of the error terms, ρ_k, have been estimated for each time series of a chamber across the entire year (Sect. 2.4).

Autocorrelation in error terms on the original scale was less strong than autocorrelation in error terms on a lognormal scale (Fig. C1). This result had at least two causes. First, on a normal scale the autocorrelation in process variation is obscured by the instrumentation error with supposedly very low autocorrelation. For the lognormal assumption low fluxes were excluded where the assumption that instrumentation error was small compared to process error was invalid (Table C1). Second, the process error terms on the original scale are exponential transforms of the process error terms. And it is harder to detect autocorrelation in nonlinear models (White, 1992).

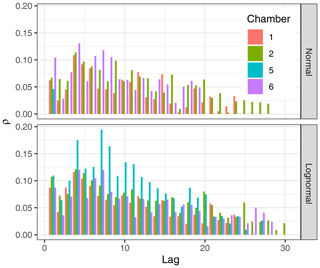
Figure C1 Empirical correlation coefficients are stronger between residuals on a log-transformed scale (bottom).

Table C1 Number of unflagged observations and number of effective records after accounting for autocorrelation in residuals.