the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Analysis and reduction of the geomagnetic gradient influence on aeromagnetic compensation in a towed bird
Zhijian Zhou
Zhilong Liu
Wenduo Li
Yihang Wang
Chao Wang
Aeromagnetic exploration is an important method of geophysical exploration. We study the compensation method of the towed bird system and establish the towed bird interference model. Due to the geomagnetic gradient changing greatly, the geomagnetic gradient is considered in the towed bird interference model. In this paper, we model the geomagnetic field gradient and analyze the influence of the towed bird system on the aeromagnetic compensation results. Finally, we apply the ridge regression method to solve the problem. We verify the feasibility of this compensation method through actual flight tests and further improve the data quality of the towed bird interference.
- Article
(623 KB) - Full-text XML
- BibTeX
- EndNote
Aeromagnetic exploration is generally used in geological research, mineral exploitation, and underground unexploded ordnance detection (Ekinci et al., 2020; Beamish and White, 2011; Doll et al., 2012). Since the magnetic field generated by the ferromagnetic material and metal-cutting geomagnetic wires on the aircraft platform will interfere with the magnetic detector, it will affect the quality of aeromagnetic survey data. Therefore, it is necessary to carry out aeromagnetic compensation (Chen et al., 2018).
In 1950, Tolles and Lawson (1950) summarized three sources related to aircraft maneuvers: the permanent field, the induced field, and the eddy current field. Leliak (1961) summarized the work of Tolles and Lawson and proposed a model of aeromagnetic compensation called the Tolles Lawson (T–L) model. As a linear solution, the T–L model faces the problem of multicollinearity (Leach, 1980; Bickel, 1979). In 1979, Bickel (1979) analyzed the multicollinearity of the T–L model and proposed a small signal solving method to reduce the linear relationship between features. In 1980, Leach used linear regression theory to study the T–L model and proposed a ridge regression algorithm to solve the multicollinearity problem in the T–L model (Leach, 1980). In recent years, the main methods to solve multicollinearity problems are the principal component analysis (Wu et al., 2018), the truncated singular value decomposition (TSVD) (Gu et al., 2013; Deng et al., 2013), the multi-model compensation method (Zhao et al., 2019), the wavelet analysis method (Deng et al., 2010; Dou et al., 2016a), and the improved recursive least-squares (Zhao et al., 2017). The above methods are all based on linear models. In 1993, Williams (1993) proposed a neural network nonlinear model to solve aeromagnetic interference, but this neural network model has an overfitting problem. On this basis, Ma et al. (2017) proposed a dual estimation compensation method of unscented Kalman filter and suppressed the problem of neural network overfitting by introducing measurement noise. Yu et al. (2021) proposed an aeromagnetic compensation model based on the generalized regression neural networks (GRNNs). The model combines linear regression and a neural network, which not only solves the insufficient fitting ability of linear regression but also weakens the influence of neural network overfitting. In practice, the measured value of the airborne magnetic sensor is the superposition of the geomagnetic field and interference field. The aeromagnetic interference value has been separated through a band-pass filter (Jia and Groom et al., 2004; Jia and Lo et al., 2004; Groom et al., 2004). However, due to the existence of a geomagnetic gradient, the filter cannot completely separate the geomagnetic field. In addition, the induced magnetic field component and the eddy current magnetic field component in the interference magnetic field are related to the geomagnetic field. Therefore, there is a strong coupling relationship between the geomagnetic field and magnetic interference (Dou et al., 2016b).
The measurement device and the electrified wire in the towed bird platform system will cause interference, so it is necessary to compensate for the interference of the towed bird platform. Because the towing bird system is affected by external factors, there are two modes of movement: swing and vibration. The swing amplitude is 10 m. The geomagnetic gradient is 0.5 nT m−1, so the interference of the geomagnetic gradient on the towed bird is an important factor. In this paper, based on the towed bird interference model, the geomagnetic gradient component is introduced and solved by the ridge regression method. Through the actual flight data verification, this method can improve the data quality of pod interference.
In the process of aeromagnetic exploration, most methods use fixed-wing platforms to compensate. When the magnetic sensor is located near the fuselage or inside the fuselage, the structure and changes of the interfering magnetic field generated by the aircraft in flight are complicated, which will also cause aeromagnetic interference (Xiu et al., 2018). To reduce the aeromagnetic interference, we used the helicopter towed bird method to conduct field test measurements in the Zhanhe area of Wudalianchi City, northern Heilongjiang Province. The towed bird is connected with the helicopter through a 30 m long rope in Fig. 1. Because the ferromagnetic material in the towed bird system will affect the measurement data of the magnetic sensor, it is necessary to compensate for the magnetic interference generated by the towed bird system. There are two kinds of motion modes in the motion process of the towed bird platform: one is the large amplitude swing mode influenced by the helicopter motion, the other is the amplitude vibration mode influenced by the wind speed. Under the joint action of the two motion modes, the measured data have interfered.
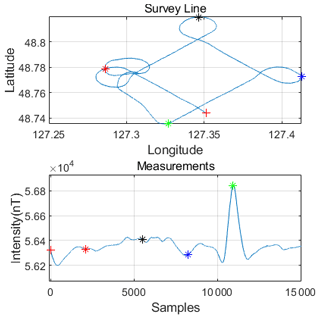
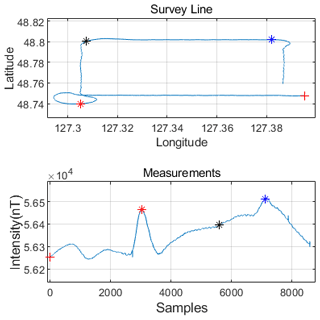
The experiment included three flights at an altitude of 1250 m. The first was a long straight flight. The purpose of the experiment was to observe the distribution of the geomagnetic field in the experimental area and the intensity of magnetic interference generated by the towed bird. Figure. 2a shows the flight path, where the survey line direction corresponds to the measured value in Fig. 2b. The swing range of the pod system platform is 10 m in Fig. 2a, and the measured value in Fig. 2b shows that the magnetic interference is about 5 nT. In Fig. 2b, the magnetic field difference between 5000–7000 sampling points is 250 nT. The distance is 500 m, so the geomagnetic gradient is 0.5 nT m−1. In Fig. 3 the diamond data are used for the training of the aeromagnetic compensation model. In Fig. 4, square data are used as the verification of the training model.
3.1 Towed bird model
The interference generated by the towed bird system and the fixed-wing helicopter platform is caused by the magnetic sensor strap-down system platform.
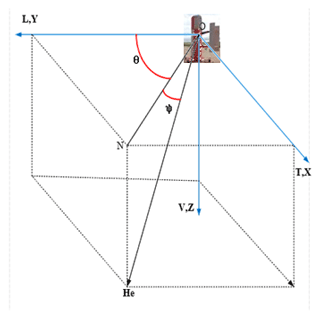
The towed bird coordinate system was established according to the fixed-wing coordinate system in Fig. 5 (Leliak, 1961). X, Y, and Z are the angles between the three coordinate axes of the towed bird and the geomagnetic field, called Euler angles, where θ and ψ are the geomagnetic declination and the geomagnetic inclination, respectively.
Euler angles X, Y, and Z can be measured by a three-axis magnetometer, and are redefined as follows:
where u1, u2, and u3 represent the direction cosine of the Euler angle.
There are three types of magnetic field interference: permanent magnetic field, induced magnetic field, and eddy current magnetic field. Refer to the T–L model to establish the towing bird jamming platform model as follows:
hI is aeromagnetic interference. ci, is the aeromagnetic interference parameter. , , is the derivative of Euler angle cosine to time.
This can be further expressed as follows:
where c=[c1 c2 c3…c16]T is the aeromagnetic interference parameter, and is the aeromagnetic interference feature.
The linear superposition of geomagnetic field and aeromagnetic interference constitutes the measured value h:
3.2 Error analysis and improvement
Traditional aeromagnetic compensation usually uses a band-pass filter to obtain the aeromagnetic interference value. bpf(R) is expressed as linear band-pass filtering for each column of matrix R. Applying bpf to both ends of Eq. (4), we can get the following results:
When bpf(He)=0, then
The data processed by the band-pass filter are denoted as hfuf. Let . Then Eq. (6) can be expressed as follows:
Applying the least-squares method solves the following:
where is the generalized inverse of the matrix uf, denoted as .
To analyze the influence of the system matrix uf on the result, we perform singular value decomposition on the system matrix uf:
where the matrix uf is R×16 matrix. U and V are R×R and 16×16 orthogonal matrices respectively. S is R×16 diagonal matrix. σAi is the ith singular value and has . uAi is the ith column vector of matrix U. vAi is the ith column vector of matrix V.
Then, the least-squares solution (Eq. 8) can be expressed as follows:
It can be obtained from the above formula that the system matrix uf contains small singular values. The slight error in matrix hf will be magnified. During the movement, the swing distance of the towed bird is 10 m. Since the geomagnetic gradient is 0.5 nT m−1, it will introduce the geomagnetic gradient, resulting in the presence of the geomagnetic field component in the filtered aeromagnetic interference hf, which will cause an error in the solution.
From the above analysis, it can be known that the existence of the geomagnetic gradient will affect the compensation result of the towed bird interference. According to the two-dimensional Taylor model of the geomagnetic field, the horizontal geomagnetic field is expressed as a function of latitude x and longitude y (Dawson and Newitt, 1977).
where (He)hor is the horizontal geomagnetic field. x0 and y0 are the latitude and longitude of the initial position, cmk is a constant, and N is the truncation order.
The filtered horizontal geomagnetic field obtained through band-pass filter processing is as follows:
The Taylor model only considers the relationship between latitude and longitude and the geomagnetic field but does not consider the influence of altitude changes on the geomagnetic field. Since the helicopter's flying height is 1250 m, it is considered that the vertical geomagnetic field gradient is proportional to the helicopter's flying height. Assuming that the scale factor of the vertical gradient component of the geomagnetic field is v, the filtered vertical gradient component can be expressed as follows:
where bpf((He)ver) is the filtered vertical geomagnetic field gradient value. z0 is the height of the starting position of the towed bird, and z is the height of the towed bird during flight. Then the geomagnetic field passing through the band-pass filter can be further expressed as follows:
When the truncation order N is different, the expression of Eq. (14) will be different, which will affect the final compensation result.
Next, we use a band-pass filter to filter the truncation order :
By introducing Eq. (14) into Eq. (5), we can get the following results:
bpf((He)hor) can bring in different results according to different values of N in Eq. (14) and finally combine the towed bird model with the geomagnetic field model. The final expression is as follows:
where and . uθ and cθ have different expressions according to the value of N. For example, when N=1, and .
Since the T–L model introduces the geomagnetic field component, the model will further have a multicollinearity problem. Therefore, the ridge regression method is introduced to solve this problem. The ridge regression solution formula is as follows:
where is the parameter estimation value under the ridge regression, and λ is the regularization factor.
3.3 Evaluation standard of compensation quality
The traditional aeromagnetic compensation quality evaluation standard uses a standard deviation improvement ratio to evaluate the following:
σbefore and σafter are the standard deviations of the data before and after compensation, respectively. Standard deviation data include not only aeromagnetic interference data but also geomagnetic gradient data. Assuming that the aeromagnetic interference and the geomagnetic field can be linearly superimposed, then
and are the standard deviations of the aeromagnetic interference before and after compensation. and are the standard deviations of the geomagnetic field before and after compensation. The aeromagnetic interference caused by birds is small, but the geomagnetic gradient is large and changes a little before and after compensation.
Therefore,
Therefore, the data before and after compensation are filtered by a band-pass filter with a cut-off frequency of 0.03–0.1 Hz.
Then there are
The paper takes IR as the evaluation index of the compensation result.
According to the above analysis, when the truncation order of the two-dimensional Taylor model of the local magnetic field is , the ridge regression method is used to solve Eq. (17). The standard deviation IR of Eq. (22) is used to evaluate the results of aeromagnetic compensation.
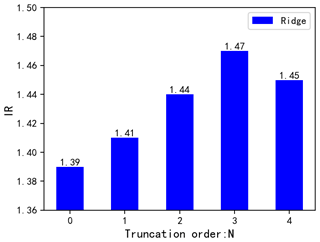
Figure 6 shows the standard deviation improvement ratio of applying the ridge regression method when the truncation order N is 0, 1, 2, 3, 4 respectively. The paper selects the truncation order of the two-dimensional Taylor of the geomagnetic field. When N=0, the compensation result is less than the standard deviation improvement rate when N is 1, 2, 3. When N is 4, it will be slightly lower than the standard deviation improvement ratio when N is 3. When the truncation order is greater than 3, the multicollinearity of the model will increase, leading to the introduction of errors in the solution process, so choosing a suitable truncation order is very important for model solving. When N is 3, the ridge regression method is used to solve the problem, and the final compensation result is the best. The standard deviation improvement is 6 % higher than that of the compensation effect without the geomagnetic gradient.
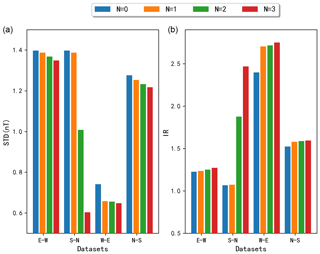
Figure 7Comparison of compensation results of in different directions: (a) standard deviation (SD) and (b) improvement ratio (IR).
Figure 7 shows the comparison of the standard deviation and improvement ratio of the towed bird compensation in different directions. Figure 8 shows the comparison of the compensation result when . It can be seen from Figs. 7 and 8 that when the helicopter is flying in the south and west directions, the standard deviation is large, the towing bird swing is small, and the main interference is vibration mode. Therefore, when the geomagnetic gradient is introduced into the compensation, the result is only slightly better than the model when N=1. When the helicopter is heading north, because the towing bird platform is affected by swing and vibration, it is greatly affected by the geomagnetic gradient, resulting in large aeromagnetic interference. Introducing the geomagnetic gradient into the towed bird interference model will be improved, and IR will be improved to 2.47. When the helicopter is heading east, the interference is mainly caused by the swing mode of the towed bird. The standard deviation interference is small, and it is greatly affected by the geomagnetic gradient. So the IR is improved to 2.75.
The paper analyzes two movement modes of the towed bird system during the movement process. We considered the influence of geomagnetic gradient changes on the results of aeromagnetic interference compensation, but we also introduced the varying geomagnetic gradients into the interference model. Finally, we derive the model parameter estimation and correction. The paper solves the problem of the compensation result of the geomagnetic gradient change under the towing bird system but also expands the towing bird interference model. When the towed bird system is subject to large swings and vibrations in the heading, this method can improve the data quality of aeromagnetic interference; the experimental results show that the improvement ratio has increased by 6 %. Next, we will use this compensation method to improve the data quality of aeromagnetic surveys and use the helicopter towed bird system to detect underground magnetic targets.
The data presented in this study are available on request from the corresponding author. The data are not publicly available because the measurement area contains sensitive information.
This research was designed, tested and implemented by the authors of the paper. The paper was designed and wrote by ZZ and ZL. The other three authors (WL, YW and CW) carried out revision and correction during the completion of the article. All authors have read and agreed to the published version of the paper.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by the Key Projects of National Key R&D Programs for Major Natural Disaster Monitoring, Early Warning and Prevention (grant no. 2018YFC1503803), and the Key Technology Research of optically pumped magnetometer based on semi-conductor laser under Grant 41304140.
This paper was edited by Lev Eppelbaum and reviewed by two anonymous referees.
Beamish, D. and White, J. C.: Aeromagnetic data in the UK: A study of the information content of baseline and modern surveys across anglesey, north wales: Aeromagnetic data, anglesey, Geophys. J. Int., 184, 171–190, https://doi.org/10.1111/j.1365-246X.2010.04852.x, 2011.
Bickel, S. H.: Small signal compensation of magnetic fields resulting from aircraft maneuvers, IEEE T. Aero. Elec. Sys., AES-15, 518–525, https://doi.org/10.1109/TAES.1979.308736, 1979.
Chen, L., Wu, P., Zhu, W., Feng, Y., and Fang, G.: A novel strategy for improving the aeromagnetic compensation performance of helicopters, Sensors, 18, 1846, https://doi.org/10.3390/s18061846, 2018.
Dawson, E. and Newitt, L. R.: An analytical representation of the geomagnetic field in canada for 1975. part I: The main field, Can. J. Earth Sci., 14, 477–487, https://doi.org/10.1139/e77-046, 1977.
Deng, P., Lin, C., Tan, B., and Zhang, J.: Application of adaptive filtering algorithm based on wavelet transformation in aeromagnetic survey, Paper presented at the 3rd International Conference on Computer Science and Information Technology, 2 492–496, https://doi.org/10.1109/ICCSIT.2010.5564839, 2010.
Deng, P., Lin, C. S., and Zhang, J.: Research on aircraft magnetic compensation based on improved singular value decomposition, Appl. Mech. Mater., 281, 41–46, https://doi.org/10.4028/www.scientific.net/AMM.281.41, 2013.
Doll, W. E., Gamey, T. J., Bell, D. T., Beard, L. P., Sheehan, J. R., Norton, J., Holladay, J. S., and Lee, J. L. C.: Historical development and performance of airborne magnetic and electromagnetic systems for mapping and detection of unexploded ordnance, J. Environ. Eng. Geoph., 17, 1–17, https://doi.org/10.2113/JEEG17.1.1, 2012.
Dou, Z., Han, Q., Niu, X., Peng, X., and Guo, H.: An adaptive filter for aeromagnetic compensation based on wavelet multiresolution analysis, IEEE Geosci. Remote S., 13, 1069–1073, https://doi.org/10.1109/LGRS.2016.2565685, 2016a.
Dou, Z., Han, Q., Niu, X., Peng, X., and Guo, H.: An aeromagnetic compensation coefficient-estimating method robust to geomagnetic gradient, IEEE Geosci. Remote S., 13, 611–615, https://doi.org/10.1109/LGRS.2015.2512927, 2016b.
Ekinci, Y. L., Büyüksaraç, A., Bektaş, Ö., and Ertekin, C.: Geophysical investigation of mount nemrut stratovolcano (bitlis, eastern turkey) through aeromagnetic anomaly analyses, Pure Appl. Geophys., 177, 3243–3264, https://doi.org/10.1007/s00024-020-02432-0, 2020.
Groom, R. W., Jia, Z. R., and Lo, B.: Magnetic compensation of magnetic noises related to aircraft's maneuvers in airborne survey, presented at the 17th EEGS Symposium Application Geophysics Engineering Environmental Problems, Ottawa, ON, Canada, 2004.
Gu, B., Li, Q., and Liu, H.: Aeromagnetic compensation based on truncated singular value decomposition with an improved parameter-choice algorithm, Paper presented at the 6th International Congress on Image and Signal Processing (CISP), 3 1545–1551, https://doi.org/10.1109/CISP.2013.6743921, 2013.
Jia, J. R., Groom, R. W., and Lo, B.: The use of GPS sensors and numerical improvements in aeromagnetic compensation. SEG Technical Program Expanded Abstracts, 23, 1221–1224, https://doi.org/10.1190/1.1839661, 2004.
Jia, Z. R., Lo, B., and Groom, R. W.: Final Report on Improved Aeromagnetic Compensation. Ontario Mineral Exploration Technol. Program, Ottawa, ON, Canada, Project P02-03-043, https://doi.org/10.13140/RG.2.1.2072.0402, 2004.
Leach, B. W.: Aeromagnetic Compensation as a Linear Regression Problem, Academic Press, New York, 139–161, 1980.
Leliak, P.: Identification and evaluation of magnetic-field sources of magnetic airborne detector equipped aircraft, IRE Transactions on Aerospace and Navigational Electronics, ANE-8, 95–105, https://doi.org/10.1109/TANE3.1961.4201799, 1961.
Ma, M., Zhou, Z., and Cheng, D.: A dual estimate method for aeromagnetic compensation, Meas. Sci. Technol., 28, 115904, https://doi.org/10.1088/1361-6501/aa883b, 2017.
Tolles, W. E. and Lawson, J. D.: Magnetic compensation of MAD equipped aircraft, Airbone Instrum. Lab. Inc., Mineola, NY, USA, Rep. 201, 1950.
Williams, P. M.: Aeromagnetic compensation using neural networks, Neural Comput. Appl., 1, 207–214, https://doi.org/10.1007/BF01414949, 1993.
Wu, P., Zhang, Q., Chen, L., Zhu, W., and Fang, G.: Aeromagnetic compensation algorithm based on principal component analysis, J. Sensors, 2018, 1–7, https://doi.org/10.1155/2018/5798287, 2018.
Xiu, C., Meng, X., Guo, L., Zhang, S., and Zhang, X.: Compensation for aircraft effects of magnetic gradient tensor measurements in a towed bird, Explor. Geophys., 49, 713–725, https://doi.org/10.1071/EG16028, 2018.
Yu, P., Zhao, X., Jiao, J., Jia, J., and Zhou, S.: An improved neural network method for aeromagnetic compensation, Meas. Sci. Technol., 32, 45106, https://doi.org/10.1088/1361-6501/abd1b4, 2021.
Zhao, G., Shao, Y., Han, Q., and Tong, X.: A novel aeromagnetic compensation method based on the improved recursive least-squares, Paper presented at the Advances in Intelligent Information Hiding and Multimedia Signal Processing, 64 171–178, https://doi.org/10.1007/978-3-319-50212-0_21, 2017.
Zhao, G., Han, Q., Peng, X., Zou, P., Wang, H., Du, C., Wang, H., Tong, X., Li, Q., and Guo, H.: An aeromagnetic compensation method based on a multimodel for mitigating multicollinearity, Sensors, 19, 2931, https://doi.org/10.3390/s19132931, 2019.