Accuracies of field CO₂–H₂O data from open-path eddy-covariance flux systems: assessment based on atmospheric physics and biological environment

Ecosystem CO₂–H₂O data measured by infrared gas analyzers in open-path eddy-covariance (OPEC) systems have numerous applications, such as estimations of CO₂ and H₂O fluxes in the atmospheric boundary layer. To assess the applicability of the data for these estimations, data uncertainties from analyzer measurements are needed. The uncertainties are sourced from the analyzers in zero drift, gain drift, cross-sensitivity, and precision variability. These four uncertainty sources are individually specified for analyzer performance, but so far no methodology exists yet to combine these individual sources into a composite uncertainty for the specification of an overall accuracy, which is ultimately needed. Using the methodology for closed-path eddy-covariance systems, this overall accuracy for OPEC systems is determined from all individual uncertainties via an accuracy model and further formulated into CO₂ and H₂O accuracy equations. Based on atmospheric physics and the biological environment, for EC150 infrared CO₂–H₂O analyzers, these equations are used to evaluate CO₂ accuracy (±1.22 mgCO₂ m⁻³, relatively ±0.19 %) and H₂O accuracy (±0.10 gH₂O m⁻³, relatively ±0.18 % in saturated air at 35 ^∘C and 101.325 kPa). Both accuracies are applied to conceptual models addressing their roles in uncertainty analyses for CO₂ and H₂O fluxes. For the high-frequency air temperature derived from H₂O density along with sonic temperature and atmospheric pressure, the role of H₂O accuracy in its uncertainty is similarly addressed. Among the four uncertainty sources, cross-sensitivity and precision variability are minor, although unavoidable, uncertainties, whereas zero drift and gain drift are major uncertainties but are minimizable via corresponding zero and span procedures during field maintenance. The accuracy equations provide rationales to assess and guide the procedures. For the atmospheric background CO₂ concentration, CO₂ zero and CO₂ span procedures can narrow the CO₂ accuracy range by 40 %, from ±1.22 to ±0.72 mgCO₂ m⁻³. In hot and humid weather, H₂O gain drift potentially adds more to the H₂O measurement uncertainty, which requires more attention. If H₂O zero and H₂O span procedures can be performed practically from 5 to 35 ^∘C, the H₂O accuracy can be improved by at least 30 %: from ±0.10 to ±0.07 gH₂O m⁻³. Under freezing conditions, the H₂O span procedure is impractical but can be neglected because of its trivial contributions to the overall uncertainty. However, the zero procedure for H₂O, along with CO₂, is imperative as an operational and efficient option under these conditions to minimize H₂O measurement uncertainty.

1 Introduction

Open-path eddy-covariance (OPEC) systems are used most in quantity to measure boundary-layer CO₂, H₂O, heat, and momentum fluxes between ecosystems and the atmosphere (Lee and Massman, 2011). For flux measurements, an OPEC system is equipped with a fast-response three-dimensional (3-D) sonic anemometer, to measure 3-D wind velocities and sonic temperature (T_s), and a fast-response infrared CO₂–H₂O analyzer (hereafter referred to as an infrared analyzer or analyzer) to measure CO₂ and H₂O concentrations or densities (Fig. 1). In this system, the analyzer is adjacent to the sonic measurement volume. Both anemometer and analyzer together provide synchronized high-frequency (e.g., 10 to 20 Hz) measurements, which are used to compute the fluxes at a location represented by the measurement volume (Aubinet et al., 2012). Given that the measurement conditions, which are spatially homogenous in flux sources/sinks and temporally steady in turbulent flows without advection, satisfy the underlying theory for eddy-covariance flux techniques (Katul et al., 2004; Finnigan, 2008), the quality of each flux data point primarily depends on the exactness of field measurements of the variables, such as CO₂, H₂O, T_s, and 3-D wind, at the sensor sensing scales (Foken et al., 2012; Richardson et al., 2012), although the quality may also be degraded by other biases if not fully corrected. In an OPEC system, other biases are commonly sourced from the tilt of the vertical axis of the sonic anemometer away from the vertical vector of natural wind (Kaimal and Haugen, 1969), the spatial separation between the anemometer and the analyzer (Laubach and McNaughton, 1998), the line and/or volume averaging of measurements (Wyngaard, 1971; Andreas, 1981), the response delay of sensors to fluctuations in measured variables (Horst, 2000), the air density fluctuations due to heat and water vapor transfer (Webb et al., 1980), and the filtering in data processing (Rannik and Vesala, 1999). These biases are theoretically correctable through coordinate rotation corrections for the tilt (Tanner and Thurtell, 1969; Wilczak et al., 2001); covariance lag maximization for the separation (Moncrieff et al., 1997; Ibrom et al., 2007); low- and high-frequency corrections for the data filtering, line and/or volume averaging, and response delay (Moore, 1986; Lenschow et al., 1994; Massman, 2000; van Dijk, 2002); and Webb–Pearman–Leuning (WPL) corrections for the air density fluctuations (Webb et al., 1980). Even though these corrections are thorough for corresponding biases, errors in the ultimate flux data still exist due to uncertainties related to measurement exactness at the sensor sensing scales (Fratini et al., 2014; Zhou et al., 2018). These uncertainties are not only unavoidable because of actual or apparent instrumental drifts due to the thermal sensitivity of sensor path lengths, long-term aging of sensor detection components, and unexpected factors in field operations (Fratini et al., 2014), but they are also not mathematically correctable because their sign and magnitude are unknown (Richardson et al., 2012). The overall measurement exactness related to these uncertainties would be a valuable addition to flux data analysis (Goulden et al., 1996; Anthoni et al., 2004).

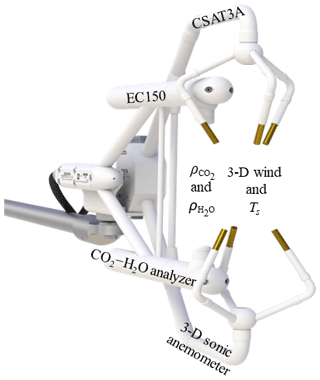
Figure 1 Integration of an EC150 infrared CO₂–H₂O analyzer for CO₂ density (${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$) and H₂O density (${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) with a CSAT3A sonic anemometer for three-dimensional (3-D) wind velocities and sonic temperature (T_s) in an open-path eddy-covariance flux system (Image credit: Campbell Scientific Inc., UT, USA).

In addition to flux computations, the data for individual variables from these field measurements can be important in numerous applications. Knowledge of measurement exactness is also required for an accurate assessment of data applicability (Csavina et al., 2017; Hill et al., 2017). The infrared analyzer in an OPEC system outputs CO₂ density (${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ in mgCO₂ m⁻³) and H₂O density (${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ in gH₂O m⁻³). For instance, ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, along with T_s and atmospheric pressure (P), can be used to derive ambient high-frequency air temperature (T_a) (Swiatek, 2018). In this case, given an exact equation of T_a in terms of the three independent variables ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, T_s, and P, the applicability of this equation to the OPEC systems for T_a depends wholly on the measurement exactness of the three independent variables. The higher the degree of exactness, the less uncertain the T_a. The assessment of the applicability necessitates the knowledge of the measurement exactness. In reality, to the best of our knowledge, neither the overall measurement exactness of ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ from the infrared analyzers nor the exactness of T_s from the sonic anemometers (Larry Jecobsen, personal communication, 2022) is available. This study defines and estimates the measurement exactness of ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ including ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ from infrared analyzers through the consolidation of the measurement uncertainties, which are not practically avoidable or mathematically correctable, although they can be minimized through analyzer maintenance.

As comprehensively reviewed by Richardson et al. (2012), numerous previous studies including Goulden et al. (1996), Lee et al. (1999), Anthoni et al. (1999, 2004), and Flanagan and Johnson (2005) have quantified various sources of flux measurement errors and have attempted to attach confidence intervals to the annual sums of net ecosystem exchange. These sources include measurement methods (e.g., sensor separation and site homogeneity; Munger et al., 2012), data processing algorithms (e.g., data filtering, Rannik and Vesala, 1999, and data gap filling, Richardson and Hollinger, 2007), measurement conditions (e.g., advection; Finnigan, 2008), energy closure (Foken, 2008), and sensor body heating effects (Burba et al., 2008). Instead of quantifying the flux errors, Foken et al. (2004, 2012) assessed the flux data quality and divided it into nine grades (1 to 9) based on steady state, turbulence conditions, and wind direction in the sonic anemometer coordinate system. The lower the grade, the smaller the error in flux data (i.e., higher flux data quality); the higher grade, the greater the error in flux data (i.e., lower flux data quality). This grade matrix (Foken et al., 2004, 2012) has been adopted by AmeriFlux (2018) for their flux data quality assessments. To correct the measurement biases from infrared analyzers, Burba et al. (2008) developed a correction method for sensor body heating effects on CO₂ and H₂O fluxes, whereas Fratini et al. (2014) developed a method for correcting the raw high-frequency CO₂ and H₂O data using the interpolated zero and span coefficients of an infrared analyzer from the analyzer maintenance such as zero and span procedures under the same conditions but at the beginning and ending of each maintenance period. The corrected data were then used to re-estimate the fluxes. Nevertheless, no study so far has addressed the overall measurement exactness of ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ or ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, which are related to the unavoidable and uncorrectable measurement uncertainties in the CO₂ and H₂O data from the infrared analyzers in OPEC systems, even though this overall measurement exactness is fundamental for data analysis in applications (Richardson et al., 2012). Therefore, instead for the overall exactness of an individual field CO₂ or H₂O measurement, the infrared analyzers are specified only for their individual CO₂ and H₂O measurement uncertainties sourced from their zero and gain drifts, cross-sensitivity to background ${\mathrm{H}}_{\mathrm{2}}\mathrm{O}/{\mathrm{CO}}_{\mathrm{2}}$, and measurement precision variability (LI-COR Biosciences, 2021c; Campbell Scientific Inc., 2021b).

For any sensor, the measurement exactness depends on its performance as commonly specified in terms of accuracy, precision, and other uncertainty descriptors such as sensor hysteresis. Conventionally, accuracy is defined as a systematic uncertainty, while precision is defined as a random measurement error (ISO, 2012, where ISO is the acronym of International Organization for Standardization). Other uncertainty descriptors are also defined for specific reliabilities in instrumental performance. For example, CO₂ zero drift is one of the descriptors specified for the performance of infrared analyzers in CO₂ measurements (Campbell Scientific Inc., 2021b). Both accuracy and precision are universally applicable to any sensor for the specification of its performance in measurement exactness. Other uncertainty descriptors are more sensor-specific (e.g., cross-sensitivity to ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ is used for infrared analyzers in OPEC and CPEC systems, where CPEC is an acronym for closed-path eddy covariance).

Conventionally, sensor accuracy is the degree of closeness to which its measurements are to the true value in the measured variable; sensor precision, related to repeatability, is the degree to which repeated measurements under unchanged conditions produce the same values (Joint Committee for Guides in Metrology, 2008). Another definition advanced by the ISO (2012), revising the conventional definition of accuracy as trueness originally representing only systematic uncertainty, specifies accuracy as a combination of both trueness and precision. An advantage of this definition for accuracy is the consolidation of all measurement uncertainties. According to this definition, the accuracy is the range of composited uncertainty from all uncertainty sources in field measurements. For CPEC systems, Zhou et al. (2021) developed a method and derived a model to assess the accuracy of ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ mixing ratio measurements of infrared analyzers. Their model was further formulated as a set of equations to evaluate the defined accuracies for CO₂ and H₂O mixing ratio data from CPEC systems. Although the CPEC systems are very different from OPEC systems in their structural designs (e.g., measurements take place inside a closed cuvette vs. in an open space) and in output variables (e.g., ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ mixing ratio vs. ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ density), similarities exist between the two systems in measurement uncertainties as specified by their manufacturers (Campbell Scientific Inc., 2021a, b) because the infrared analyzers in both systems use the same physics theories and similar optical techniques for their measurements (LI-COR Biosciences, 2021b, c). Accordingly, the method developed by Zhou et al. (2021) for CPEC systems can be reasonably applied to their OPEC counterparts with rederivation of the model and reformulation of equations. Following the methodology of Zhou et al. (2021) and using the specifications of EC150 infrared analyzers in OPEC systems as an example (Campbell Scientific Inc., 2021b), we can derive the model and formulate equations to assess the accuracies of CO₂ and H₂O measurements by infrared analyzers in OPEC systems; discuss the usage of accuracies in flux analysis, data applications, and analyzer field maintenance; and ultimately provide a reference for the flux measurement community in order to specify the overall accuracy of field ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ measurements by infrared analyzers in OPEC systems.

2 Specification implications

An OPEC system for this study includes, but is not limited to, a CSAT3A sonic anemometer and an EC150 infrared analyzer (Fig. 1). The system operates in a T_a range from −30 to 50 ^∘C and in a P range from 70 to 106 kPa. Within these operational ranges, the specifications for CO₂ and H₂O measurements (Campbell Scientific Inc., 2021b) are given in Table 1.

Table 1 Measurement specifications for EC150 infrared CO₂–H₂O analyzers (Campbell Scientific Inc., UT, USA).

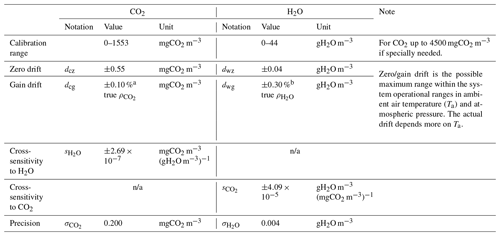
^a 0.10 % is the CO₂ gain drift percentage denoted by ${\mathit{\delta }}_{{\mathrm{CO}}_{\mathrm{2}}\mathit{\_}\mathrm{g}}$ in the text, and ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ is CO₂ density. ^b 0.30 % is the H₂O gain drift percentage denoted by ${\mathit{\delta }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathit{\_}\mathrm{g}}$ in the text, and ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is H₂O density. n/a denotes “not applicable”.

In Table 1, the top limit of 1553 mgCO₂ m⁻³ in the calibration range for CO₂ density in dry air is more than double the atmospheric background CO₂ density of 767 mgCO₂ m⁻³, or 419 µmolCO₂ mol⁻¹, where mol is the unit for dry air, reported by the Global Monitoring Laboratory (2022) with a T_a of 20 ^∘C under a P of 101.325 kPa (i.e., normal temperature and pressure, Wright et al., 2003). The top limit of 44 gH₂O m⁻³ in the calibration range for H₂O density is equivalent to a 37 ^∘C dew point, higher than the highest 35 ^∘C dew point ever recorded under natural conditions on Earth (National Weather Service, 2022).

The measurement uncertainties from infrared analyzers for CO₂ and H₂O in Table 1 are specified by individual uncertainty components along with their magnitudes: zero drift, gain drift, cross-sensitivity to ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$, and precision variability. Zero drift uncertainty is an analyzer non-zero response to zero air/gas (i.e., air/gas free of CO₂ and H₂O). Gain drift uncertainty is an analyzer trend-deviation response to a measured gas species away from its true value in proportion (Campbell Scientific Inc., 2021b). Cross-sensitivity is an analyzer response to either background CO₂ if H₂O is measured or background H₂O if CO₂ is measured. Precision variability is an analyzer random response to minor unexpected factors. For CO₂ and H₂O, these four components should be composited as an overall uncertainty in order to evaluate the accuracy, which is ultimately needed in practice.

Precision variability is a random error, and the other specifications can be regarded as trueness. Zero drifts are primarily impacted by T_a, and so are gain drifts (see the “Note” column in Table 1 and also Fratini et al., 2014). Additionally, each gain drift is also positively proportional to the true magnitude of ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ density (i.e., true ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ or true ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) under measurements. Lastly, cross-sensitivity to ${\mathrm{H}}_{\mathrm{2}}\mathrm{O}/{\mathrm{CO}}_{\mathrm{2}}$ is related to the background amount of ${\mathrm{H}}_{\mathrm{2}}\mathrm{O}/{\mathrm{CO}}_{\mathrm{2}}$ as indicated by its units: mgCO₂ m⁻³ (gH₂O m⁻³)⁻¹ for CO₂ measurements and gH₂O m⁻³ (mgCO₂ m⁻³)⁻¹ for H₂O measurements.

Accordingly, beyond statistical analysis, the accuracy of ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ measurements should be evaluated over a T_a range of −30 to 50 ^∘C, a ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ range of up to 44 gH₂O m⁻³, and a ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ range of up to 1553 mgCO₂ m⁻³.

3 Accuracy model

The measurement accuracy of infrared analyzers is the possible maximum range of overall measurement uncertainty from the four uncertainty sources as specified in Table 1: zero drift, gain drift, cross-sensitivity, and precision variability. The four uncertainties interactionally or independently contribute to the overall uncertainty in a measured value. Given the true α density (ρ_αT, where subscript α can be either CO₂ or H₂O) and measured α density (ρ_α), the difference between the true and measured α densities (Δρ_α) is given by

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}={\mathit{\rho }}_{\mathit{\alpha }}-{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}.\end{array}$$

The analyzer overestimates the true value if Δρ_α>0, exactly estimates the true value if Δρ_α=0, and underestimates the true value if Δρ_α<0. The measurement accuracy is the maximum range of Δρ_α (i.e., an accuracy range). According to the analyses of Zhou et al. (2021) for CPEC infrared analyzers, as mathematically shown in Appendix A, this range is interactionally contributed by the zero drift uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}$), gain drift uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{g}}$), and cross-sensitivity uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}$) along with an independent addition from the precision uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}$). However, any interactional contribution from a pair of uncertainties is 3 orders smaller in magnitude than each individual contribution in the pair. The contribution to the accuracy range due to interactions can be reasonably neglected. Therefore, the accuracy range can be simply modeled as a sum of the absolute values of the four component uncertainties. From Eq. (A7) in Appendix A, the measurement accuracy of α density from OPEC systems by infrared analyzers is defined in an accuracy model as

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}\equiv \pm \left(\left|\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{g}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{p}}\right|\right).\end{array}$$

Assessment of the accuracy of field CO₂ or H₂O measurements is, by the use of known and/or estimable variables, the formulation and evaluation of the four terms on the right side of this accuracy model.

4 Accuracy of CO₂ density measurements

Based on accuracy Model (2), we define the accuracy of field CO₂ measurements from OPEC systems by infrared analyzers ($\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$) as

$$\begin{array}{}\text{(3)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}& \equiv \pm (\left|\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{z}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{g}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{s}}\right|\\ & +\left|\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{p}}\right|),\end{array}\end{array}$$

where $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{z}}$ is CO₂ zero drift uncertainty, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{g}}$ is CO₂ gain drift uncertainty, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{s}}$ is cross-sensitivity-to-H₂O uncertainty, and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{p}}$ is CO₂ precision uncertainty.

CO₂ precision (${\mathit{\sigma }}_{{\mathrm{CO}}_{\mathrm{2}}}$) is the standard deviation of ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ random errors among repeated measurements under the same conditions (Joint Committee for Guides in Metrology, 2008). The random errors generally have a normal statistical distribution (Hoel, 1984). Therefore, using this deviation, the precision uncertainty for an individual CO₂ measurement at a 95 % confidence interval (P value of 0.05) can be statistically formulated as

$$\begin{array}{}\text{(4)}& \mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{p}}=\pm \mathrm{1.96}\times {\mathit{\sigma }}_{{\mathrm{CO}}_{\mathrm{2}}}.\end{array}$$

The other uncertainties, due to CO₂ zero drift, CO₂ gain drift, and cross-sensitivity to H₂O, are caused by the inability of the working equation inside the analyzer operating system (OS) to adapt to the changes in analyzer-internal and ambient environmental conditions, such as internal housing CO₂ and/or H₂O levels and ambient air temperature. From the derivations in the “Theory and operation” section in LI-COR Biosciences (2001, 2021b, c), a general model of the working equation for ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ is given by

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}& =P\sum _{i=\mathrm{1}}^{\mathrm{5}}{a}_{\mathrm{c}i}\mathit{\{}\mathrm{1}-[{\displaystyle \frac{A_{\mathrm{c}}}{A_{\mathrm{cs}}}}\\ & +S_{\mathrm{w}}\left(\mathrm{1}-{\displaystyle \frac{A_{\mathrm{w}}}{A_{\mathrm{ws}}}}\right)]Z_{\mathrm{c}}{\mathit{\}}}^i{\left\{{\displaystyle \frac{G_{\mathrm{c}}}{P}}\right\}}^i,\end{array}\end{array}$$

where subscripts c and w indicate CO₂ and H₂O, respectively; a_ci (i=1, 2, 3, 4, or 5) is a coefficient of the 5-order polynomial for the terms inside curly brackets; A_cs and A_ws are the power values of analyzer source lights at the chosen wavelengths for CO₂ and H₂O measurements, respectively; A_c and A_w are their respective remaining power values after the source lights pass through the measured air sample; S_w is cross-sensitivity of the detector to H₂O while detecting CO₂, at the wavelength for CO₂ measurements (hereafter referred to as sensitivity to H₂O); Z_c is the CO₂ zero adjustment (i.e., CO₂ zero coefficient); and G_c is the CO₂ gain adjustment (i.e., commonly known as the CO₂ span coefficient). For an individual analyzer, the parameters a_ci, Z_c, G_c, and S_w in Model (5) are statistically estimated in the production calibration against a series of standard CO₂ gases at different concentration levels over the ranges of ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and P (hereafter referred to as calibration). Since the estimated parameters are specific for the analyzer, Model (5) with these estimated parameters becomes an analyzer-specific CO₂ working equation. The working equation is used internally by the infrared analyzer to compute ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ as the closet proxy for true ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ from field measurements of A_c, A_cs, A_w, A_ws, and P.

The analyzer-specific working equation is deemed to be accurate immediately after the calibration through estimations of a_ci, Z_c, G_c, and S_w in production, while Z_c and G_c can be re-estimated in the field (LI-COR Biosciences, 2021c). However, as used internally by an optical instrument under changing environments vastly different from its calibration conditions by its manufacturer, the working equation may not be fully adaptable to the changes, which might be reflected through CO₂ zero and/or gain drifts of the deployed infrared analyzer. In the working equation for ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ from Model (5), the parameter Z_c is related to CO₂ zero drift; G_c to CO₂ gain drift; and S_w to sensitivity to H₂O. Therefore, the analyses of Z_c and G_c, along with S_w, aid in understanding the causes of CO₂ zero drift, CO₂ gain drift, and sensitivity to H₂O. Such understanding is necessary to formulate $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{z}}$, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{g}}$, and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{s}}$ in Model (3).

4.1 Z_c and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{z}}$ (CO₂ zero drift uncertainty)

In production, an infrared analyzer is calibrated for zero air/gas to report zero ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ plus an unavoidable random error. However, when using the analyzer in measurement environments that are different from calibration conditions, the analyzer often reports this zero ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, while exposed to zero air, as a value that migrates gradually away from zero and possibly beyond $\pm \mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{p}}$, which is known as CO₂ zero drift. This drift is primarily affected by a combination of three factors: (i) the temperature surrounding the analyzer away from the calibration temperature, (ii) traceable CO₂ and H₂O accumulations, such as during use, inside the analyzer light housing due to an inevitable, although small, leaking exchange of housing air with the ambient air (hereafter referred to as housing CO₂–H₂O accumulation), and (iii) aging of analyzer components (Richardson et al., 2012).

Firstly, the dependency of analyzer CO₂ zero drift on ambient air temperature arises due to a thermal expansion/contraction of analyzer components that slightly changes the analyzer geometry (Fratini et al., 2014). This change in geometry can deviate the light path length for measurement a little away from the length under manufacturer calibration, contributing to the drift. Additionally, inside an analyzer, the performance of the light source and absorption detector for measurement, as well as the electronic components for measurement control, can vary slightly with temperature. In production, an analyzer is calibrated to compensate for the ensemble of such dependencies as assessed in a calibration chamber. The compensation algorithms are implemented in the analyzer OS, which is kept as proprietary by the analyzer manufacturer. However, the response of an analyzer to a temperature varies as conditions change over time (Fratini et al., 2014). Therefore, manufacturers typically specify an expected range of typical or maximal drift per ^∘C (see Table 1 and also see the section for analyzer specifications in Campbell Scientific Inc., 2021b). Secondly, the housing CO₂–H₂O accumulation is caused by unavoidable small leaks in the light housing of an infrared analyzer. The housing is technically sealed to keep housing air close to zero air by introducing scrubber chemicals into the housing to absorb any CO₂ and H₂O that may sneak into the housing through an exchange with any ambient air (LI-COR Biosciences, 2021c). Over time, the scrubber chemicals may be saturated by CO₂ and/or H₂O or lose their active absorbing effectiveness, which can result in housing CO₂–H₂O accumulations. Thirdly, as optical components, the light source may gradually become dim, and the absorption detector may gradually become less sensitive. The accumulation and aging develop slowly and less obviously in the relatively long term (e.g., months or longer), whereas the dependencies of drift on ambient air temperature can occur quickly and more clearly as soon as an analyzer is deployed in the field (Richardson et al., 2012). Apparently, the drift with ambient air temperature is a major concern if an analyzer is maintained as scheduled by its manufacturer for the replacement of scrubber chemicals (Campbell Scientific Inc., 2021b).

Due to the CO₂ zero drift, the working equation needs to be adjusted through its parameter re-estimation to adapt the ambient air temperature near which the system is running, housing CO₂–H₂O accumulation, and analyzer component aging. This adjustment technique is the zero procedure, which brings the ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ in zero air/gas measurement back to zero as closely as possible. In this section, our discussion focuses on CO₂, and the same application to H₂O will be described in the following sections. In the field, the zero procedure should be feasibly operational using one air/gas benchmark to re-estimate one parameter in the working equation. This parameter must be adjustable to output zero ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ from the zero air/gas benchmark. By setting the left side of Model (5) to zero and rearranging it, it is clear that Z_c is such a parameter that can be adjusted to result in a zero ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ value for zero air/gas:

$$\begin{array}{}\text{(6)}& Z_{\mathrm{c}}={\left[{\displaystyle \frac{A_{\mathrm{c}\mathrm{0}}}{A_{\mathrm{cs}}}}+S_{\mathrm{w}}\left(\mathrm{1}-{\displaystyle \frac{A_{\mathrm{w}\mathrm{0}}}{A_{\mathrm{ws}}}}\right)\right]}^{-\mathrm{1}},\end{array}$$

where A_c0 and A_w0 are the counterparts of A_c and A_w for zero air/gas, respectively. For an analyzer, the zero procedure for CO₂ is thus to re-estimate Z_c in balance of Eq. (6).

If Z_c could continually balance Eq. (6) after the zero procedure, the CO₂ zero drift would not be significant; however, this is not the case. Similar to its performance after the manufacturer calibration, an analyzer may still drift after the zero procedures due to frequent changes in ambient air temperature, housing CO₂–H₂O accumulation, and/or analyzer component age. Nevertheless, the Z_c value needed for an analyzer to be punctually adaptable for these changes is unpredictable because these changes are not foreseeable. Assuming on-schedule maintenance (i.e., the scrubber chemicals inside the analyzer light housing are replaced following the manufacturer's guidelines), the housing CO₂–H₂O accumulation should not be a concern. While the ambient temperature surrounding the infrared analyzer is not controlled, the CO₂ zero drift is therefore mainly influenced by T_a and can be ±0.55 mgCO₂ m⁻³ at most within the operational ranges in T_a and P for the EC150 infrared analyzers in OPEC systems (Table 1).

Given that an analyzer performs best almost without zero drift at the ambient air temperature for the calibration/zeroing procedure (T_c) and that it possibly drifts while T_a gradually changes away from T_c, then the further away T_a is from T_c, the more it possibly drifts in the CO₂ zero. Over the operational range in P of the EC150 infrared analyzers used for OPEC systems, this drift is more proportional to the difference between T_a and T_c but is still within the specifications (Campbell Scientific Inc., 2021b). Accordingly, CO₂ zero drift uncertainty at T_a can be formulated as

$$\begin{array}{}\text{(7)}& \mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{z}}={\displaystyle \frac{d_{\mathrm{cz}}}{T_{\mathrm{rh}}-T_{\mathrm{rl}}}}\times \left\{\begin{array}{ll}{T}_{\mathrm{a}}-T_{\mathrm{c}}& T_{\mathrm{c}}<T_{\mathrm{a}}<T_{\mathrm{rh}}\\ T_{\mathrm{c}}-T_{\mathrm{a}}& T_{\mathrm{c}}>T_{\mathrm{a}}>T_{\mathrm{rl}}\end{array}\right.,\end{array}$$

where, over the operational range in T_a of EC150 infrared analyzers used for OPEC systems, T_rh is the highest-end value (50 ^∘C) and T_rl is the lowest-end value (−30 ^∘C, Table 1). $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{z}}$from this equation has the maximum range, as specified in Table 1, equal to d_cz in magnitude as if T_a and T_c were separately at the two ends of operational range in T_a of OPEC systems.

4.2 G_c and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{g}}$ (CO₂ gain drift uncertainty)

An infrared analyzer was also calibrated against a series of standard CO₂ gases. The calibration sets the working equation from Model (5) to closely follow the gain trend of change in ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$. As was determined with the zero drift, the analyzer, with changes in housing CO₂–H₂O accumulation, ambient conditions, and age during its deployment, could report CO₂ gradually drifting away from the real gain trend of the change in ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, which is specifically termed CO₂ gain drift. This drift is affected by almost the same factors as the CO₂ zero drift (Richardson et al., 2012; Fratini et al., 2014; LI-COR Biosciences, 2021c).

Due to the gain drift, the infrared analyzer needs to be further adjusted, after the zero procedure, to tune its working equation back to the real gain trend in ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ of measured air as closely as possible. This is done with the CO₂ span procedure. This procedure can be performed through use of either one or two span gases (LI-COR Biosciences, 2021c). If two are used, one span gas is slightly below the ambient CO₂ density and the other is at a much higher density to fully cover the CO₂ density range by the working equation. However, commonly, like the zero procedure, this procedure is simplified by the use of one CO₂ span gas, as a benchmark, with a known CO₂ density (${\stackrel{\mathrm{̃}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}}$) around the typical CO₂ density values in the measurement environment. If one CO₂ span gas is used, only one parameter in the working equation is available for adjustment. Weighing the gain of the working equation more than any other parameter, this parameter is the CO₂ span coefficient (G_c) (see Model 5). The CO₂ span gas is used to re-estimate G_c to satisfy the following equation (for details, see LI-COR Biosciences, 2021c):

$$\begin{array}{}\text{(8)}& \left|{\stackrel{\mathrm{̃}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}}-{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}\left(G_{\mathrm{c}}\right)\right|\le min\left|{\stackrel{\mathrm{̃}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}}-{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}\right|.\end{array}$$

Similar to the zero drift, the CO₂ gain drift continues after the CO₂ span procedure. Based on a similar consideration for the specifications of CO₂ zero drift, the CO₂ gain drift is specified by the maximum CO₂ gain drift percentage (${\mathit{\delta }}_{{\mathrm{CO}}_{\mathrm{2}}\mathit{\_}\mathrm{g}}=\mathrm{0.10}$ %) associated with ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ as ±0.10 % × (true ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$) (Table 1). This specification is the maximum range of CO₂ measurement uncertainty due to the CO₂ gain drift within the operational ranges in T_a and P of the EC150 infrared analyzers in OPEC systems.

Given that an analyzer performs best, almost without gain drift, at the ambient air temperature for calibration/span procedures (also denoted by T_c because zero and span procedures should be performed under similar ambient air temperature conditions) but also drifts while T_a gradually changes away from T_c, then the further away T_a is from T_c, the greater potential that the analyzer drifts. Accordingly, the same approach to the formulation of CO₂ zero drift uncertainty can be applied to the formulation of the approximate equation for CO₂ gain drift uncertainty at T_a as

$$\begin{array}{}\text{(9)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{g}}& =\pm {\displaystyle \frac{{\mathit{\delta }}_{{\mathrm{CO}}_{\mathrm{2}}\mathit{\_}\mathrm{g}}{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}}{T_{\mathrm{rh}}-T_{\mathrm{rl}}}}\\ & \times \left\{\begin{array}{ll}{T}_{\mathrm{a}}-T_{\mathrm{c}}& T_{\mathrm{c}}<T_{\mathrm{a}}<T_{\mathrm{rh}}\\ T_{\mathrm{c}}-T_{\mathrm{a}}& T_{\mathbf{c}}>T_{\mathrm{a}}>T_{\mathrm{rl}}\end{array}\right.,\end{array}\end{array}$$

where ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}$ is the true CO₂ density unknown in measurement. Given that the measured value of CO₂ density is represented by ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, by referencing Eq. (1), ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}$ can be expressed as

$$\begin{array}{}\text{(10)}& {\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}={\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}-(\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{z}}+\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{g}}+\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{s}}+\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{p}}).\end{array}$$

The terms inside the parentheses in this equation are the measurement uncertainties for ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}$ that are smaller in magnitude, by at least 2 orders, than ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}$, whose magnitude in atmospheric background under the normal temperature and pressure as used by Wright et al. (2003) is 767 mgCO₂ m⁻³ (Global Monitoring Laboratory, 2022). Therefore, ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ in Eq. (10) is the best alternative, with the greatest likelihood, to ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}$ for the application of Eq. (9). As such, ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}$ in Eq. (9) can be reasonably approximated by ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ for equation applications. Using this approximation, Eq. (9) becomes

$$\begin{array}{}\text{(11)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{g}}& =\pm {\displaystyle \frac{{\mathit{\delta }}_{{\mathrm{CO}}_{\mathrm{2}}\mathit{\_}\mathrm{g}}{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}}{T_{\mathrm{rh}}-T_{\mathrm{rl}}}}\\ & \times \left\{\begin{array}{ll}{T}_{\mathrm{a}}-T_{\mathrm{c}}& T_{\mathrm{c}}<T_{\mathrm{a}}<T_{\mathrm{rh}}\\ T_{\mathrm{c}}-T_{\mathrm{a}}& T_{\mathrm{c}}>T_{\mathrm{a}}>T_{\mathrm{rl}}\end{array}\right..\end{array}\end{array}$$

With ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ being measured, this equation is applicable in estimating the CO₂ gain drift uncertainty. The gain drift uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{g}}$) from this equation has the maximum range of $\pm {\mathit{\delta }}_{{\mathrm{CO}}_{\mathrm{2}}\mathit{\_}\mathrm{g}}{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, as if T_a and T_c were separately at the two ends of operational range in T_a of OPEC systems. With the greatest likelihood, this maximum range is the closest to $\pm {\mathit{\delta }}_{{\mathrm{CO}}_{\mathrm{2}}\mathit{\_}\mathrm{g}}$ × (true ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$) as specified in Table 1.

4.3 S_w and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{s}}$ (sensitivity-to-H₂O uncertainty)

The infrared wavelength of 4.3 µm for CO₂ measurements is minorly absorbed by H₂O (LI-COR Biosciences, 2021c; Campbell Scientific Inc., 2021b). This minor absorption slightly interferes with the absorption by CO₂ in the wavelength (McDermitt et al., 1993). The power of the same measurement light (i.e., A_cs as a steady value in the CO₂ working equation from Model 5) through several gas samples with the same CO₂ density, but different backgrounds of H₂O densities, is detected with different values of A_c in the working equation from Model (5). Without parameter S_w and its joined term in the working equation, different A_c values must result in significantly different ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ values, although they are actually the same. In case of the same CO₂ density in the airflows under different H₂O backgrounds, the different values of A_c to report similar ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ are accounted for by S_w associated with A_w and A_ws in the working equation from Model (5). Similar to Z_c and G_c in the CO₂ working equation, S_w is not perfectly accurate and can have uncertainty in the determination of ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$. This uncertainty for EC150 infrared analyzers is specified by sensitivity to H₂O ($s_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) as $\pm \mathrm{2.69}\times {\mathrm{10}}^{-\mathrm{7}}$ mgCO₂ m⁻³ (gH₂O m⁻³)⁻¹ (Table 1). As indicated by its unit, this uncertainty is linearly related to ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$. Assuming the analyzer for CO₂ works best, without this uncertainty, in dry air, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{s}}$ could be formulated as

$$\begin{array}{}\text{(12)}& \mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{s}}=s_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\mathrm{0}\le {\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\le \mathrm{44}{\mathrm{gH}}_{\mathrm{2}}\mathrm{O}{\mathrm{m}}^{-\mathrm{3}},\end{array}$$

where 44 gH₂O m⁻³, as addressed in Sect. 2, is the top limit of H₂O density measurements. Accordingly, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{s}}$ can be in the range of

$$\begin{array}{}\text{(13)}& \mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{s}}\le \mathrm{44}\left|s_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\right|.\end{array}$$

4.4 $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ (CO₂ measurement accuracy)

Substituting Eqs. (4), (7), (11), and (13) into Model (3), $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ for an individual CO₂ measurement from OPEC systems by infrared analyzers can be expressed as

$$\begin{array}{}\text{(14)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}& =\pm [\mathrm{1.96}{\mathit{\sigma }}_{{\mathrm{CO}}_{\mathrm{2}}}+\mathrm{44}\left|s_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\right|\\ & +{\displaystyle \frac{\left|d_{\mathrm{cz}}\right|+{\mathit{\delta }}_{{\mathrm{CO}}_{\mathrm{2}}\mathit{\_}\mathrm{g}}{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}}{T_{\mathrm{rh}}-T_{\mathrm{rl}}}}\\ & \times \left\{\begin{array}{ll}{T}_{\mathrm{a}}-T_{\mathrm{c}}& T_{\mathrm{c}}<T_{\mathrm{a}}<T_{\mathrm{rh}}\\ T_{\mathrm{c}}-T_{\mathrm{a}}& T_{\mathrm{c}}>T_{\mathrm{a}}>T_{\mathrm{rl}}\end{array}\right.].\end{array}\end{array}$$

This is the CO₂ accuracy equation for the infrared analyzers within OPEC systems. It expresses the accuracy of a field CO₂ measurement from the OPEC systems in terms of the analyzer specifications ${\mathit{\sigma }}_{{\mathrm{CO}}_{\mathrm{2}}}$, $s_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, d_cz, ${\mathit{\delta }}_{{\mathrm{CO}}_{\mathrm{2}}\mathit{\_}\mathrm{g}}$, and the OPEC system operational range in T_a as indicated by T_rh and T_rl, measured variables ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and T_a, and a known variable T_c. Given the specifications and the known variable, this equation can be used to evaluate the CO₂ accuracy as a range in relation to T_a and ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$.

4.5 Evaluation of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$

Given the analyzer specifications, the accuracy of field CO₂ measurements from an infrared analyzer after calibration, zero, and/or span at T_c can be evaluated using the CO₂ accuracy Eq. (14) over a domain of T_a and ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$. To visualize the relationship of accuracy with T_a and ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, the accuracy is presented better as the ordinate along the abscissa of T_a for ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ at different levels and must be evaluated within possible maximum ranges of T_a and ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ in ecosystems. In evaluation, the T_a is limited to the −30 to 50 ^∘C range within which EC150 infrared analyzers used for OPEC systems operate, T_c can be assumed to be 20 ^∘C (i.e., standard air temperature as used by Wright et al., 2003), and ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ can range according to its variation in ecosystems.

4.5.1 ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ range

The upper measurement limit of CO₂ density by the infrared analyzers can reach up to 1553 mgCO₂ m⁻³. In the atmosphere, its background CO₂ mixing ratio is currently 419 µmolCO₂ mol⁻¹ (Global Monitoring Laboratory, 2022). Under normal temperature and pressure conditions (Wright et al., 2003), this background mixing ratio is equivalent to 767 mgCO₂ m⁻³ in dry air. The CO₂ density in ecosystems commonly ranges from 650 to 1500 mgCO₂ m⁻³ (LI-COR Biosciences, 2021c), depending on biological processes (Wang et al., 2016), aerodynamic regimes (Yang et al., 2007), and thermodynamic states (Ohkubo et al., 2008). In this study, this range is extended from 600 to 1600 mgCO₂ m⁻³ as a common range within which $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ is evaluated. Because of the dependence of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ on ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ (Eq. 14), to show the accuracy at different CO₂ levels, the range is further divided into five grades of 600, 767 (atmospheric background), 1000, 1300, and 1600 mgCO₂ m⁻³ for evaluation presentations as in Fig. 2.

According to a brief review by Zhou et al. (2021) on the plant physiological threshold in air temperature for growth and development and the soil temperature dynamic related to CO₂ from microorganism respiration and/or wildlife activities in terrestrial ecosystems, ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ at any grade of 1000, 1300, or 1600 mgCO₂ m⁻³ should, at 5 ^∘C, start to converge asymptotically to the atmospheric CO₂ background (767 mgCO₂ m⁻³ at −30 ^∘C, Fig. 2). Without an asymptotical function for the convergence curve, conservatively assuming the convergence has a simple linear trend with T_a from 5 to −30 ^∘C, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ is evaluated up to the magnitude of ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ along the trend (Fig. 2).

4.5.2 $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ range

At T_a=T_c, the CO₂ accuracy is best at its narrowest range to be the sum of precision and sensitivity-to-H₂O uncertainties (±0.39 mgCO₂ m⁻³). However, away from T_c, its range near-linearly becomes wider. The $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ range can be summarized as ±0.40 to ±1.22 mgCO₂ m⁻³ over the domain of T_a and ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ (Fig. 2a and CO₂ columns in Table 2). The maximum CO₂ relative accuracy at the different levels of ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ is in a range of ±0.07 % at 1600 mgCO₂ m⁻³ to 0.19 % at 600 mgCO₂ m⁻³ (from data for Fig. 2b).

Figure 2 Accuracy of field CO₂ measurements from open-path eddy-covariance flux systems by EC150 infrared CO₂–H₂O analyzers (Campbell Scientific Inc., UT, USA) over their operational range in T_a at atmospheric pressure of 101.325 kPa. The vertical dashed line represents ambient air temperature T_c at which an analyzer was calibrated, zeroed, and/or spanned. Above 5 ^∘C, accuracy is evaluated up to the possible maximum CO₂ density in ecosystems (black curves). Assume that this maximum CO₂ density starts linearly decreasing at 5 ^∘C to the atmospheric CO₂ background value 767 mgCO₂ m⁻³ at −30 ^∘C. Accordingly, below 5 ^∘C, the accuracy for CO₂ density at a level above the background value (green, blue, or black curves) is evaluated up to this decreasing trend of CO₂ densities. Relative accuracy of CO₂ measurements is the ratio of CO₂ accuracy to CO₂ density.

Table 2 Accuracies of field CO₂ and H₂O measurements from open-path eddy-covariance systems by EC150 infrared CO₂–H₂O analyzers (Campbell Scientific Inc., UT, USA) on the major background values of ambient air temperature, CO₂, and H₂O in ecosystems. (Atmospheric pressure: 101.325 kPa. Calibration ambient air temperature: 20 ^∘C.)

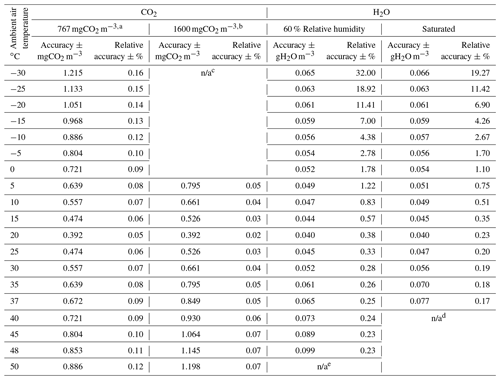
^a 767 mgCO₂ m⁻³ is the atmospheric background CO₂ density (Global Monitoring Laboratory, 2022). ^b 1600 mgCO₂ m⁻³ is assumed to be the maximum CO₂ density in ecosystems. ^c CO₂ density in ecosystems is assumed to be lower than 1600 mgCO₂ m⁻³ when ambient air temperature is below 5 ^∘C. ^d H₂O density in saturated air above 37 ^∘C is out of the measurement range of EC150 infrared CO₂–H₂O analyzers (0–44 gH₂O m⁻³). ^e H₂O density in air of 60 % relative humidity above 48 ^∘C is out of the measurement range of EC150 infrared CO₂–H₂O analyzers (0–44 gH₂O m⁻³). n/a denotes “not applicable”.

5 Accuracy of H₂O density measurements

Model (2) defines the accuracy of field H₂O measurements from OPEC systems by infrared analyzers ($\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) as

$$\begin{array}{}\text{(15)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}& \equiv \pm (\left|\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{z}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{g}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{s}}\right|\\ & +\left|\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{p}}\right|),\end{array}\end{array}$$

where$\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{z}}$ is H₂O zero drift uncertainty, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{g}}$ is H₂O gain drift uncertainty, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{s}}$ is cross-sensitivity-to-CO₂ uncertainty, and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{p}}$ is H₂O precision uncertainty. Using the same approach as for $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{p}}$, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{p}}$ is formulated as

$$\begin{array}{}\text{(16)}& \mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^P=\pm \mathrm{1.96}\times {\mathit{\sigma }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}},\end{array}$$

where ${\mathit{\sigma }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, as defined in Table 1, is the precision of the infrared analyzers for H₂O measurements. The other uncertainty terms in Model (15) can be understood and formulated using a similar approach for their counterparts in Model (3).

5.1 $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{z}}$ (H₂O zero drift uncertainty) and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{g}}$ (H₂O gain drift uncertainty)

The model of the analyzer working equation for ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is similar to Model (5) for ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ in formulation, given also by the derivations in the “Theory and operation” section in LI-COR Biosciences (2001, 2021b, c):

$$\begin{array}{}\text{(17)}& \begin{array}{rl}{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}& =P\sum _{i=\mathrm{1}}^{\mathrm{3}}{a}_{\mathrm{w}i}\mathit{\{}\mathrm{1}-[{\displaystyle \frac{A_{\mathrm{w}}}{A_{\mathrm{ws}}}}\\ & +S_{\mathrm{c}}\left(\mathrm{1}-{\displaystyle \frac{A_{\mathrm{c}}}{A_{\mathrm{cs}}}}\right)]Z_{\mathrm{w}}{\mathit{\}}}^i{\left\{{\displaystyle \frac{G_{\mathrm{w}}}{P}}\right\}}^i,\end{array}\end{array}$$

where a_wi (i=1, 2, or 3) is a coefficient of the 3-order polynomial in the terms inside curly brackets; S_c is the cross-sensitivity of a detector to CO₂, while detecting H₂O, at the wavelength for H₂O measurements (hereafter referred to as sensitivity to CO₂); Z_w is the H₂O zero adjustment (i.e., H₂O zero coefficient); G_w is the H₂O gain adjustment (i.e., commonly referred as to H₂O span coefficient); and A_w, A_ws, A_c, and A_cs represent the same things as in Model (5). The parameters of a_wi, Z_w, G_w, and S_c in Model (17) are statistically estimated to establish an H₂O working equation in the production calibration against a series of air standards with different H₂O contents under ranges of ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and P (i.e., calibration). The H₂O working equation (i.e., Model 17 with estimated parameters) is used inside the analyzer OS to compute ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ as the closest proxy for true ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ from field measurements of A_w, A_ws, A_c, A_cs, and P.

Because of the similarities in model principles and parameter implications between Models (5) and (17), following the same analyses and rationales as for $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{z}}$ and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{g}}$, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{z}}$ is formulated as

$$\begin{array}{}\text{(18)}& \mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{z}}={\displaystyle \frac{d_{\mathrm{wz}}}{T_{\mathrm{rh}}-T_{\mathrm{rl}}}}\times \left\{\begin{array}{ll}{T}_{\mathrm{a}}-T_{\mathrm{c}}& T_{\mathrm{c}}<T_{\mathrm{a}}<T_{\mathrm{rh}}\\ T_{\mathrm{c}}-T_{\mathrm{a}}& T_{\mathrm{c}}>T_{\mathrm{a}}>T_{\mathrm{rl}}\end{array}\right.,\end{array}$$

and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{g}}$ is formulated as

$$\begin{array}{}\text{(19)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{g}}& =\pm {\displaystyle \frac{{\mathit{\delta }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathit{\_}\mathrm{g}}{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{T_{\mathrm{rh}}-T_{\mathrm{rl}}}}\\ & \times \left\{\begin{array}{ll}{T}_{\mathrm{a}}-T_{\mathrm{c}}& T_{\mathrm{c}}<T_{\mathrm{a}}<T_{\mathrm{rh}}\\ T_{\mathrm{c}}-T_{\mathrm{a}}& T_{\mathrm{c}}>T_{\mathrm{a}}>T_{\mathrm{rl}}\end{array}\right..\end{array}\end{array}$$

5.2 $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{s}}$ (sensitivity-to-CO₂ uncertainty)

The infrared light at wavelength of 2.7 µm for H₂O measurement is traceably absorbed by CO₂ (see Fig. 4.7 in Wallace and Hobbs, 2006). This absorption interferes slightly with the H₂O absorption at this wavelength (McDermitt et al., 1993). As such, the power of identical measurement lights (i.e., A_ws as a steady value in the H₂O working equation from Model 17) through several air standards with the same H₂O density but different backgrounds of CO₂ amounts would result in different values of A_w in the H₂O working equation from Model (17). In this equation, without parameter S_c and its joined term, different A_w values will result in significantly different ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ values, although ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is essentially the same. In case of the same H₂O amount in the airflows under different CO₂ backgrounds, different values of A_w reporting the same ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ are accounted for by S_c associated with A_c and A_cs in the H₂O working equation from Model (17). However, S_c is not perfectly accurate either, having uncertainty in the determination of ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$. This uncertainty in the EC150 infrared analyzer is specified by the sensitivity to CO₂ ($s_{{\mathrm{CO}}_{\mathrm{2}}}$) as the maximum range of $\pm \mathrm{4.09}\times {\mathrm{10}}^{-\mathrm{5}}$ gH₂O m⁻³ (mgCO₂ m⁻³)⁻¹ (Table 1). Assuming the infrared analyzers for H₂O have the lowest sensitivity-to-CO₂ uncertainty for airflow with an atmospheric background CO₂ amount (i.e., 767 mgCO₂ m⁻³), $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{s}}$ could be formulated as

$$\begin{array}{}\text{(20)}& \begin{array}{rl}& \mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{s}}=s_{{\mathrm{CO}}_{\mathrm{2}}}\left({\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}-\mathrm{767}\right)\\ & {\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}\le \mathrm{1553}{\mathrm{mgCO}}_{\mathrm{2}}{\mathrm{m}}^{-\mathrm{3}}.\end{array}\end{array}$$

Accordingly, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{s}}$ can be reasonably expressed as

$$\begin{array}{}\text{(21)}& \left|\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{s}}\right|\le \mathrm{786}{s}_{{\mathrm{CO}}_{\mathrm{2}}}.\end{array}$$

5.3 $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ (H₂O measurement accuracy)

Substituting Eqs. (16), (18), (19), and (21) into Model (15), $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ for an individual H₂O measurement from OPEC systems by infrared analyzers can be expressed as

$$\begin{array}{}\text{(22)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}& =\pm [\mathrm{1.96}{\mathit{\sigma }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}+\mathrm{786}\left|s_{{\mathrm{CO}}_{\mathrm{2}}}\right|\\ & +{\displaystyle \frac{\left|d_{\mathrm{wz}}\right|+{\mathit{\delta }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathit{\_}\mathrm{g}}{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{T_{\mathrm{rh}}-T_{\mathrm{rl}}}}\\ & \times \left\{\begin{array}{ll}{T}_{\mathrm{a}}-T_{\mathrm{c}}& T_{\mathrm{c}}<T_{\mathrm{a}}<T_{\mathrm{rh}}\\ T_{\mathrm{c}}-T_{\mathrm{a}}& T_{\mathrm{c}}>T_{\mathrm{a}}>T_{\mathrm{rl}}\end{array}\right.].\end{array}\end{array}$$

This equation is the H₂O accuracy equation for the OPEC systems with infrared analyzers. It expresses the accuracy of H₂O measurements from the OPEC systems in terms of the analyzer specifications ${\mathit{\sigma }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, $s_{{\mathrm{CO}}_{\mathrm{2}}}$, d_wz, ${\mathit{\delta }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathit{\_}\mathrm{g}}$, T_rh, and T_rl; measured variables ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ and T_a; and a known variable T_c. Using this equation and the specification values as in Table 1 for EC150 infrared analyzers, the accuracy of field H₂O measurements can be evaluated as a range for OPEC systems with such analyzers. For an OPEC system with another model of open-path infrared analyzer, such as the LI-7500 series (LI-COR Biosciences, NE, USA) or IRGASON (Campbell Scientific Inc., UT, USA), its corresponding specification values are used.

5.4 Evaluation of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$

H₂O accuracy ($\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) can be evaluated using the H₂O accuracy equation over a domain of T_a and ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$. Similar to the CO₂ accuracy equation in Fig. 2, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is presented as the ordinate along the abscissa of T_a at different ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ levels within the ranges of T_a and ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ in ecosystems (Fig. 3). As with the evaluation of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, T_a is limited from −30 to 50 ^∘C and T_c can be assumed to be 20 ^∘C. The range of ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ at T_a needs to be determined using atmospheric physics (Buck, 1981).

5.4.1 ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ range

The EC150 analyzers were calibrated for H₂O density from 0 to 44 gH₂O m⁻³ due to the reason addressed in Sect. 2. The highest limit of measurement range for H₂O density by other models of analyzers also should be near 44 gH₂O m⁻³. However, due to the positive exponential dependence of air water vapor saturation on T_a (Wallace and Hobbs, 2006), ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ has a range that is wider at higher T_a and narrower at lower T_a. Below 37 ^∘C at 101.325 kPa, ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ is lower than 44 gH₂O m⁻³, and its range becomes narrower and narrower, reaching 0.34 gH₂O m⁻³ at −30 ^∘C. To determine the H₂O accuracy over the same relative range of air moisture, even at different T_a, the saturation water vapor density is used to scale air moisture to 20 %, 40 %, 60 %, 80 %, and 100 % (i.e., relative humidity or RH). For each scaled RH value, ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ can be calculated at different T_a and P (Appendix B) for use in the H₂O accuracy equation. In this way, over the range of T_a, H₂O accuracy can be shown as curves, along each of which RH is equal (Fig. 3).

5.4.2 $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ range

In the same way as with CO₂ accuracy, the H₂O accuracy at T_a=T_c is best at its narrowest as the sum of precision and sensitivity-to-CO₂ uncertainties (<0.040 gH₂O m⁻³ in magnitude). However, away from T_c, its range non-linearly becomes wider, very gradually below this T_c value but more abruptly above because, as T_a increases, ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ at the same RH increases exponentially (Eqs. B1 and B2 in Appendix B), while $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ increases linearly with ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ in the H₂O accuracy Eq. (22). This range can be summarized as the widest at 48 ^∘C as ±0.099 gH₂O m⁻³ for air with 60 % RH (Fig. 3a and H₂O columns in Table 2). The number can be rounded up to ±0.10 gH₂O m⁻³ for the overall accuracy of field H₂O measurements from OPEC systems by the EC150 infrared analyzers.

Figure 3b shows an interesting trend of H₂O relative accuracy with T_a. Given the RH range, as shown in Fig. 3b, the relative accuracy diverges with a T_a decrease and converges with a T_a increase. The H₂O relative accuracy varies from 0.17 % for saturated air at 37 ^∘C to 96 % for 20 % RH air at −30 ^∘C (data for Fig. 3b) and, at this low T_a, can be much greater if RH goes further lower. The H₂O relative accuracy in magnitude is <1 % while ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}>\mathrm{5.00}$ gH₂O m⁻³, <5 % while ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}>\mathrm{1.20}$ gH₂O m⁻³, and >10 % while ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}<\mathrm{0.60}$ gH₂O m⁻³.

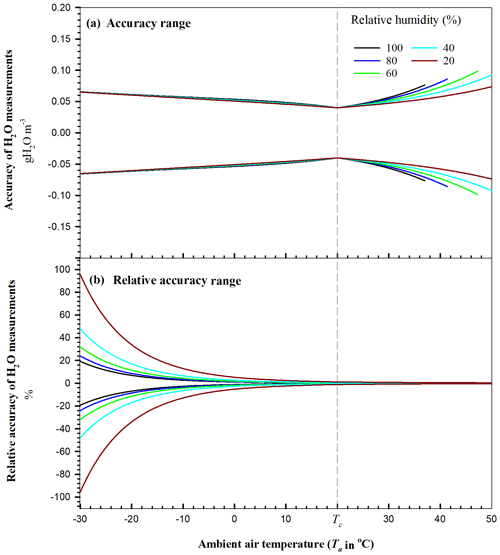
Figure 3 Accuracy of field H₂O measurements from open-path eddy-covariance systems by EC150 infrared CO₂–H₂O analyzers (Campbell Scientific Inc., UT, USA) over their operational range in T_a under atmospheric pressure of 101.325 kPa. The vertical dashed line represents the ambient air temperature (T_c) at which an analyzer was calibrated, zeroed, and/or spanned. Relative accuracy of H₂O measurements is the ratio of H₂O accuracy to H₂O density.

6 Application

The primary objective of this study is to develop an assessment methodology to evaluate the overall accuracies of field CO₂ and H₂O measurements from the infrared analyzers in OPEC systems by compositing their individual measurement uncertainties as specified with four uncertainty descriptors: zero drift, gain drift, sensitivity to ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$, and precision variability (Table 1). Ultimately, the overall accuracies (i.e., $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) make uncertainty analyses possible for the various applications of CO₂ and H₂O data, and the composited accuracy equations (i.e., Eqs. 14 and 22) make the field maintenance rationale for infrared analyzers.

6.1 Application of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ to the uncertainty analyses for CO₂ and H₂O flux data

As discussed in Introduction, the uncertainty in each flux data point is contributed by numerous sub-uncertainties in the processes of measurements and computations, among which $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ are two fundamental uncertainties in the measurements from infrared analyzers. For this study topic, assuming 3-D wind speeds are accurately measured by a sonic anemometer, Appendix C demonstrates that neither $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ nor $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ brings an uncertainty into the covariance of vertical wind speed (w) with ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, or T_a even after coordinate rotations, lag maximization, and low- and high-frequency corrections, given by Eqs. (C8) and (C9) in Appendix C as

$$\begin{array}{}\text{(23)}& \begin{array}{rl}& {\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\prime }\right)}}_{\mathrm{rmf}}={\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}^{\prime }\right)}}_{\mathrm{rmf}},\\ & {\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\prime }\right)}}_{\mathrm{rmf}}={\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}^{\prime }\right)}}_{\mathrm{rmf}},\\ & {\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{a}}^{\prime }\right)}}_{\mathrm{rmf}}={\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{aT}}^{\prime }\right)}}_{\mathrm{rmf}},\end{array}\end{array}$$

where the overbar is a Reynolds' averaging operator, prime denotes the fluctuations in a variable away from its mean (e.g., $w_i^{\prime }=w_i-\stackrel{\mathrm{‾}}{w}$), subscript T indicates “true” value (see Appendix C for the implication of true value), and subscript rmf indicates that the covariance was corrected through coordinate rotations (r), lag maximization (m), and low- and high-frequency corrections (f). The three equalities in Eq. (23) that are proved in Appendix C prove that the measured covariance of w with ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, or T_a is not affected by corresponding $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, or ΔT_a (i.e., accuracy of T_a), being equal to the true covariance. Further, through WPL corrections, the three terms on the left side of Eq. (23) can be used to derive an analytical equation for measured CO₂ or H₂O flux, whereas the three terms on the right side of this equation can be used to derive an analytical equation for true CO₂ or H₂O flux. The comparison of both analytical equations can demonstrate the partial effects of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ on the uncertainty in CO₂ or H₂O flux data.

6.1.1 Roles of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ in the uncertainty in CO₂ flux data

Using the terms on the left side of Eq. (23), through the WPL corrections for CO₂ flux from ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\prime }\right)}}_{\mathrm{rmf}}$ (Webb et al., 1980), the measured CO₂ flux ($F_{{\mathrm{CO}}_{\mathrm{2}}}$) is given by

$$\begin{array}{}\text{(24)}& \begin{array}{rl}{F}_{{\mathrm{CO}}_{\mathrm{2}}}& ={\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}^{\prime }\right)}}_{\mathrm{rmf}}+[\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{d}}}}{\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\prime }\right)}}_{\mathrm{rmf}}\\ & +\left(\mathrm{1}+\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{d}}}}\right){\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}}}{{\stackrel{\mathrm{‾}}{T}}_{\mathrm{aK}}}}{\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{a}}^{\prime }\right)}}_{\mathrm{rmf}}],\end{array}\end{array}$$

where μ is the ratio of dry air to water molecular weight, ρ_d is dry air density, and T_aK is air temperature in kelvin. According to Eqs. (C1) and (23), this equation can be written as

$$\begin{array}{}\text{(25)}& \begin{array}{rl}{F}_{{\mathrm{CO}}_{\mathrm{2}}}& ={\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}T}^{\prime }\right)}}_{\mathrm{rmf}}+[\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}-\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}{\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\prime }\right)}}_{\mathrm{rmf}}\\ & +\left(\mathrm{1}+\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}-\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}\right){\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}}}{{\stackrel{\mathrm{‾}}{T}}_{\mathrm{aKT}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{T}}_{\mathrm{a}}}}{\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{a}}^{\prime }\right)}}_{\mathrm{rmf}}],\end{array}\end{array}$$

where $\mathrm{\Delta }{\stackrel{\mathrm{‾}}{T}}_{\mathrm{a}}$ is the accuracy of ${\stackrel{\mathrm{‾}}{T}}_{\mathrm{aK}}$. $\mathrm{\Delta }{\stackrel{\mathrm{‾}}{T}}_{\mathrm{a}}$ is well defined as ±0.20 K in compliance with the WMO standard (WMO, 2018). According to Eqs. (23) and (24), from ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}^{\prime }\right)}}_{\mathrm{rmf}}$, the nominal true CO₂ flux ($F_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}$) can be given by

$$\begin{array}{}\text{(26)}& \begin{array}{rl}{F}_{{\mathrm{CO}}_{\mathrm{2}}T}& ={\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}T}^{\prime }\right)}}_{\mathrm{rmf}}+[\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}}}{\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\prime }\right)}}_{\mathrm{rmf}}\\ & +\left(\mathrm{1}+\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}}}\right){\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}}{{\stackrel{\mathrm{‾}}{T}}_{\mathrm{aKT}}}}{\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{a}}^{\prime }\right)}}_{\mathrm{rmf}}].\end{array}\end{array}$$

From Eqs. (25) and (26), the uncertainty in CO₂ flux ($\mathrm{\Delta }{F}_{{\mathrm{CO}}_{\mathrm{2}}}$) can be expressed as

$$\begin{array}{}\text{(27)}& \begin{array}{rl}\mathrm{\Delta }{F}_{{\mathrm{CO}}_{\mathrm{2}}}& =F_{{\mathrm{CO}}_{\mathrm{2}}}-F_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}\\ & =\mathit{\mu }\left({\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}-\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}-{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}}}\right){\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\prime }\right)}}_{\mathrm{rmf}}\\ & +\left[\right(\mathrm{1}+\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}-\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}){\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}}}{{\stackrel{\mathrm{‾}}{T}}_{\mathrm{aKT}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{T}}_{\mathrm{a}}}}\\ & -\left(\mathrm{1}+\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}}}\right){\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{CO}}_{\mathrm{2}}\mathrm{T}}}{{\stackrel{\mathrm{‾}}{T}}_{\mathrm{aKT}}}}]{\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{a}}^{\prime }\right)}}_{\mathrm{rmf}}.\end{array}\end{array}$$

This derivation provides a conceptual model for the partial effects of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ on the uncertainty in CO₂ flux data. This uncertainty is added by $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ and $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ interactively with the density effect due to H₂O flux (i.e., the term with ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\prime }\right)}}_{\mathrm{rmf}}$ in Eq. 27) and temperature flux (i.e., the term with ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{a}}^{\prime }\right)}}_{\mathrm{rmf}}$ in Eq. 27).

6.1.2 $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ on uncertainty in H₂O flux data

Using the same approach to Eq. (27), the uncertainty in H₂O flux ($\mathrm{\Delta }{F}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) can be expressed as

$$\begin{array}{}\text{(28)}& \begin{array}{rl}\mathrm{\Delta }{F}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}& =\mathit{\mu }\left({\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}-\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}-{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}}}\right){\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\prime }\right)}}_{\mathrm{rmf}}\\ & +[\left(\mathrm{1}+\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}-\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}\right){\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}{{\stackrel{\mathrm{‾}}{T}}_{\mathrm{aKT}}+\mathrm{\Delta }{\stackrel{\mathrm{‾}}{T}}_{\mathrm{a}}}}\\ & -\left(\mathrm{1}+\mathit{\mu }{\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}}{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathrm{dT}}}}\right){\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathrm{T}}}{{\stackrel{\mathrm{‾}}{T}}_{\mathrm{aT}}}}]{\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{a}}^{\prime }\right)}}_{\mathrm{rmf}}.\end{array}\end{array}$$

This formulation provides a conceptual model for the partial effects of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ on the uncertainty in H₂O flux data. This uncertainty is added only by $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ also interactively with the density effect due to H₂O flux (i.e., the term with ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\prime }\right)}}_{\mathrm{rmf}}$ in Eq. 28) and temperature flux (the term with ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{a}}^{\prime }\right)}}_{\mathrm{rmf}}$ in Eq. 28). Further analysis and more discussion about Eqs. (27) and (28) go beyond the scope of this study.

6.2 Application of $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ to the uncertainty analysis for high-frequency air temperature

The measured variables ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, along with T_s and P, can be used to compute high-frequency T_a in OPEC systems (Swiatek, 2018). If $T_{\mathrm{a}}({\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}},T_{\mathrm{s}},P)$ were an exact function from the theoretical principles, it would not have any error itself. However, in our applications, variables ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, T_s, and P are measured from the OPEC systems experiencing seasonal climates. As addressed in this study, the measured values of these variables have measurement uncertainty in ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ ($\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, i.e., accuracy of field H₂O measurement), in T_s (ΔT_s, i.e., accuracy of field T_s measurement), and in P (ΔP, i.e., accuracy of field P measurement). The uncertainties from the measurements propagate to the computed T_a as an uncertainty (ΔT_a, i.e., accuracy of $T_{\mathrm{a}}({\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}},T_{\mathrm{s}},P)$). This accuracy is a reference by any application of T_a. It should be specified through the relationship of ΔT_a to $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, ΔT_s, and ΔP.

As field measurement uncertainties, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, ΔT_s, or ΔP are reasonably small increments in numerical analysis (Burden et al., 2016). As such, depending on all the small increments, ΔT_a is a total differential of $T_{\mathrm{a}}({\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}},T_{\mathrm{s}},P)$ with respect to ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, T_s, and P, which are measured independently by three sensors, given by

$$\begin{array}{}\text{(29)}& \mathrm{\Delta }{T}_{\mathrm{a}}={\displaystyle \frac{\partial T_{\mathrm{a}}}{\partial {\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}}}\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}+{\displaystyle \frac{\partial T_{\mathrm{a}}}{\partial T_{\mathrm{s}}}}\mathrm{\Delta }{T}_{\mathrm{s}}+{\displaystyle \frac{\partial T_{\mathrm{a}}}{\partial P}}\mathrm{\Delta }P.\end{array}$$

In this equation, $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ from the application of Eq. (22) is a necessary term to acquire ΔT_a, ΔT_s can be acquired from the specifications for 3-D sonic anemometers (Zhou et al., 2018), ΔP can be acquired from the specifications for the barometer used in the OPEC systems (Vaisala, 2020), and the three partial derivatives can be derived from the explicit function $T_{\mathrm{a}}({\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}},T_{\mathrm{s}},P)$. With $\mathrm{\Delta }{\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, ΔT_s, ΔP, and the three partial derivatives,ΔT_a can be ranged as a function of ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, T_s, and P.

6.3 Application of accuracy equations in analyzer field maintenance

An infrared analyzer performs better if the field environment is near its manufacturing conditions (e.g., T_a at 20 ^∘C), which is demonstrated in Figs. 2a and 3a for measurement accuracies associated with T_c. As indicated by the accuracies in both figures, the closer to T_c at 20 ^∘C T_a is, the better the analyzers perform. However, the analyzers are used in OPEC systems mostly for long-term field campaigns through four-seasonal climates vastly different from those in the manufacturing processes. Over time, an analyzer gradually drifts in some ways and needs field maintenance, although within its specifications.

The field maintenance cannot improve the sensitivity-to-${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ uncertainty and precision variability, but both are minor (their sum <0.392 mgCO₂ m⁻³ for CO₂, Eqs. 4 and 13; <0.045 gH₂O m⁻³ for H₂O, Eqs. 16 and 21) as compared to the zero or gain drift uncertainties. However, the zero and gain drift uncertainties are major in the determination of field ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ measurement accuracy (Figs. 2 to 4 and Eqs. 14 and 22), but they are adjustable, through the zero and/or span procedures, and can be minimized. Therefore, manufacturers of infrared analyzers have provided software and hardware tools for the procedures (Campbell Scientific Inc., 2021b) and scheduled the procedures using those tools (LI-COR Biosciences, 2021c). Fratini et al. (2014) provided a technique implemented into the EddyPro^® Eddy Covariance Software (LI-COR Biosciences, 2021a) to correct the drift biases from a raw time series of CO₂ and H₂O data through post-processing. This study provides rationales for how to assess, schedule, and perform the zero and span procedures (Figs. 2a, 3a, and 4).

Figure 4 Component measurement uncertainties due to the zero and gain drifts of EC150 infrared CO₂–H₂O analyzers (Campbell Scientific Inc, UT, USA) in open-path eddy-covariance flux systems over their operational range in T_a under an atmospheric pressure of 101.325 kPa. The vertical dashed line represents the ambient air temperature (T_c) at which an analyzer was calibrated, zeroed, and/or spanned.

6.3.1 CO₂ zero and span procedures

Figure 4a shows that the CO₂ zero drift uncertainty linearly increases with T_a away from T_c over the full T_a range within which OPEC systems operate; so, too, does CO₂ gain drift uncertainty increase for a given CO₂ concentration. As suggested by Zhou et al. (2021), both drifts should be adjusted near the T_a value around which the system runs. The zero and gain drifts should be adjusted, through zero and span procedures, at a T_a close to its daily mean around which the system runs. Based on the range of T_a daily cycle, the procedures are set at a moderate instead of the highest or lowest moment in T_a. Given the daily cycle range is much narrower than 40 ^∘C, an OPEC system could run at T_a within ±20 of T_c if the procedures are performed at a right moment of T_a. For our case study on atmospheric CO₂ background (left CO₂ column in Table 2), the procedures can narrow the widest possible range of ±1.22 mgCO₂ m⁻³ for field CO₂ measurement by at least 40 % to ±0.72 mgCO₂ m⁻³ (i.e., accuracy at 0 or 40 ^∘C when T_c=20 ^∘C), which would be a significant improvement to ensure field CO₂ measurement accuracy through CO₂ zero and span procedures.

6.3.2 H₂O zero and span procedures

Figure 4b shows that the H₂O zero drift uncertainty increases as T_a moves away from T_c in the same trend as CO₂ zero drift uncertainty. Therefore, an H₂O zero procedure can be performed by the same technique as for the CO₂ zero procedure. H₂O gain drift uncertainty has a different trend. It exponentially diverges, as T_a increases away from T_c, to $\pm \mathrm{5.0}\times {\mathrm{10}}^{-\mathrm{2}}$ gH₂O m⁻³ near 50 ^∘C and gradually converges to 2 orders smaller as T_a decreases away from T_c, to $\pm \mathrm{6.38}\times {\mathrm{10}}^{-\mathrm{4}}$ gH₂O m⁻³ at −30 ^∘C (data for Fig. 4b). The exponential divergence results from the linear relationship of H₂O gain drift uncertainty (Eq. 19) with ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$, which exponentially increases (Eq. B1) with a T_a increase away from T_c for the same RH (Buck, 1981). The convergence results from the linear relationship offset by the exponential decrease in ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ with a T_a decrease for the same RH. This trend of H₂O gain drift uncertainty with T_a is a rationale to guide the H₂O span procedure, which adjusts the H₂O gain drift.

The H₂O span procedure needs standard moist air with known H₂O density from a dew point generator. The generator is not operational near or below freezing conditions (LI-COR Biosciences, 2004), which limits the span procedure to be performed only under non-freezing conditions. This condition, from 5 to 35 ^∘C, may be considered for the generator to be conveniently operational in the field. Accordingly, the zero and span procedures for H₂O should be discussed separately for a T_a above and below 5 ^∘C.

T_a above 5 ^∘C

Looking at the right portion with T_a above 5 ^∘C in Fig. 4b, H₂O gain drift has a more obvious impact on measurement uncertainty in a higher T_a range (e.g., above T_c), within which the H₂O span procedure is most needed. In this range, the maximum accuracy range of ±0.10 gH₂O m⁻³ can be narrowed by 30 % to ±0.07 (assessed from data for Fig. 3a) if the zero and span procedures for H₂O can be sequentially performed as necessary in a T_a range from 5 to 35 ^∘C.

T_a below 5 ^∘C

Looking at the left portion with T_a below 5 ^∘C in Fig. 4b, H₂O gain drift has a less obvious contribution to the measurement uncertainty in a lower T_a range (e.g., below 5 ^∘C), within which the H₂O span procedure may be unnecessary. An H₂O gain drift uncertainty at 5 ^∘C is 50 % of the H₂O zero drift uncertainty (dotted curve in Fig. 5). This percentage decreases to 3 % at −30 ^∘C. On average, this percentage over a range of −30 to 5 ^∘C is 18 % (assessed from data for the dotted curve in Fig. 5). Thus, for H₂O measurements over the lower T_a range, it can be concluded that H₂O zero drift is a major uncertainty source, and H₂O gain drift is a minor uncertainty source.

A close examination of the other curves in Fig. 5 for the portion in the accuracy range from H₂O zero/gain drift makes this conclusion more convincing. Given T_c=20, in the accuracy range, the portion from H₂O zero drift uncertainty is much greater (maximum 38 % at −30 ^∘C) than that from H₂O gain drift uncertainty (maximum only 7 % at 5 ^∘C). On average over the lower T_a range, the former is 27 % and the latter only 4 %. Further, given T_c=5 ^∘C, in the accuracy range, the portion from H₂O gain drift uncertainty is even smaller (maximum only 3 % at −5 ^∘C); in contrast, the portion from zero drift uncertainty is more major (1 order higher, 30 % at −30 ^∘C). On average over the lower T_a range, the minor gain drift uncertainty is 1.7 %, and the major zero drift uncertainty is 17 %. Both percentages underscore that the H₂O span procedure is reasonably unnecessary under cold/dry conditions, and, under such conditions, the H₂O zero procedure is the only necessary option to efficiently minimize H₂O measurement uncertainty from the infrared analyzers in OPEC systems. This finding gives confidence in H₂O measurement accuracy to users who are worried about H₂O span procedures for infrared analyzers in the cold seasons when a dew point generator is not operational in the field (LI-COR Biosciences, 2004).

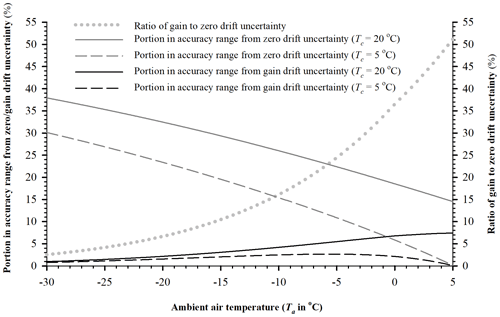
Figure 5 For a range of low T_a, the portion in the accuracy range from zero/gain drift uncertainty (left ordinate) and the ratio of gain to zero drift uncertainty (right ordinate). The curves are evaluated by Eqs. (18), (19), and (22) from measurement specifications for EC150 infrared CO₂–H₂O analyzers (Campbell Scientific Inc, UT, USA) in open-path eddy-covariance flux systems over the T_a range from −30 to 5 ^∘C under atmospheric pressure of 101.325 kPa. T_c is the ambient air temperature at which an analyzer was calibrated, zeroed, and/or spanned.

6.3.3 H₂O zero procedure in cold and/or dry environments

In cold environments, although the non-operational H₂O span procedure is unnecessary, the H₂O zero procedure is asserted to be a prominently important option for minimizing the H₂O measurement uncertainty from the infrared analyzers in OPEC systems. This procedure, although operational under freezing conditions, is still inconvenient for users when the weather is very cold (e.g., when T_a is below −15 ^∘C). If the field H₂O zero procedure is performed as needed above this T_a value, while an OPEC system runs at T_a within ±20 ^∘C of T_c, the poorest H₂O accuracy of ±0.066 gH₂O m⁻³ below 5 ^∘C in Table 2 can be narrowed, through the H₂O zero procedure, by at least 22 % to 0.051 gH₂O m⁻³ (assessed from data for Fig. 3a). Correspondingly, the relative accuracy range can be narrowed by the same percentage. The H₂O zero procedure can ensure both accuracy and relative accuracy of H₂O measurements in a cold environment (Fratini et al., 2014). In a dry environment, it plays the same role as in a cold environment, but it would be more convenient for users to perform the zero procedure if warmer.

In a cold and/or dry environment, H₂O zero procedures on a regular schedule would best minimize the impact of zero drifts on measurements. Under such an environment, the automatic zero procedure for CO₂ and H₂O together in CPEC systems is an operational and efficient option to ensure and improve field CO₂ and H₂O measurement accuracies (Campbell Scientific Inc., 2021a; Zhou et al., 2021).

7 Discussion

An assessment methodology to evaluate the overall accuracies of field CO₂ and H₂O measurements from the infrared analyzers in OPEC systems is developed using individual analyzer measurement uncertainties as specified using four uncertainty descriptors: zero drift, gain drift, sensitivity to ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$, and precision variability (Table 1). For the evaluation, these uncertainty descriptors are comprehensively composited into the accuracy Model (2) and then formulated as a CO₂ accuracy Eq. (14) and an H₂O accuracy Eq. (22) (Sects. 3 to 5 and Appendix A). The assessment methodology, along with the model and the equations, presents our development for the objective (Sects. 4.5 and 5.4).

7.1 Accuracy model

Accuracy Model (2) composites the four measurement uncertainties (zero drift, gain drift, sensitivity to ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$, and precision variability), specified for analyzer performance, as an accuracy range. This range is modeled as a simple addition of the four uncertainties. The simple addition is derived from our analysis assertion that the four measurement uncertainties interactionally or independently contribute to the accuracy range, but the contributions from the interactions inside any pair of uncertainties are negligible since they are 3 orders smaller in magnitude than an individual contribution in the pair (Appendix A). This derived model is simple and applicable, paving an approach to the formulation of accuracy equations that are computable for evaluating the overall accuracies of field CO₂ and H₂O measurements from the infrared analyzers in OPEC systems.

Additionally, included in the accuracy model, the four types of measurement uncertainty sources (i.e., zero drift, gain drift, sensitivity to ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$, and precision variability) to specify the performance of infrared CO₂–H₂O analyzers for OPEC systems have been consistently used over last 2 decades (LI-COR Biosciences, 2001, 2021b, c; Campbell Scientific Inc., 2021a, b). With the advancement of optical technologies, the number of these uncertainty sources for analyzer specifications is not expected to increase; rather some current uncertainty sources could be eliminated from the current specification list, even if not in the near future. If eliminated, in Models (3) and (15) and Eqs. (14) and (22), the parameters and variables related to the eliminated uncertainty sources could be easily removed for the adoption of the new set of specifications for infrared CO₂–H₂O analyzers.

7.2 Formulation of uncertainty terms in Model (2) for accuracy equations

In Sects. 4 and 5, each of the four uncertainty terms in accuracy Model (2) is formulated as a computable sub-equation for CO₂ (Eqs. 4, 7, 11, and 13) and H₂O (Eqs. 16, 18, 19, and 21), respectively. The accuracy model, whose terms are replaced with the formulated sub-equations for CO₂, becomes a CO₂ accuracy Eq. (14) and, for H₂O, becomes an H₂O accuracy Eq. (22). In the formulation, approximation is used for zero drift, gain drift, and sensitivity to ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$, while statistics are applied for precision variability.

For the zero/gain drift, although it is well known that the drift is influenced more by T_a if housing CO₂–H₂O accumulation is assumed to be minimized as insignificant under normal field maintenance (LI-COR Biosciences, 2021c; Campbell Scientific Inc., 2021b), the exact relationship of drift to T_a does not exist. Alternatively, the zero/gain drift uncertainty is formulated by an approximation of drifts away from T_c linearly in proportion to the difference between T_a and T_c but within its maximum range over the operational range in T_a of OPEC systems (Eqs. 7, 11, 18, and 19). A drift uncertainty equation formulated through such an approximation is not an exact relationship of drift to T_a, but it does represent the drift trend, as influenced by T_a, to be understood by users. The accuracy from this equation at a given T_a is not exact either, but the maximum range over the full range, which is the greatest-likelihood estimation, is most needed by users.

In fact, the H₂O accuracy as influenced by the linear trend of zero and gain drifts with the difference between T_a and T_c is overshadowed by the exponential trend of saturated H₂O density with T_a (Fig. 4b). Similarly, the CO₂ accuracy as influenced by the linear trend of zero and gain drifts with this difference is dominated by the CO₂ density of the ecosystem background with T_a, particularly in the low temperature range (Fig. 2). Ultimately, the assumed linear trend does not play a dominant role in the accuracy trends of CO₂ and H₂O, which shows the merits of our methodology in the uses of atmospheric physics and biological environment principles for the field data.

The sensitivity-to-${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ uncertainty can be formally formulated as Eqs. (20) or (12), but, if directly used, this formulation would add an additional variable to the ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ accuracy equation. Equation (12) would add H₂O density (${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$) to the CO₂ accuracy Eq. (14), and Eq. (20) would add CO₂ density (${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$) to the H₂O accuracy Eq. (22). For either accuracy equation, the additional variable would complicate the uncertainty analysis. According to the ecosystem environment background, the maximum range of sensitivity-to-${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ uncertainty is known, and as compared to the major uncertainty in zero/gain drift (Table 1), this range is narrow (Table 1 and Eqs. 13 and 21). Therefore, the sensitivity-to-${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ uncertainty is approximated as Eq. (21) or (13). This approximation widens the accuracy range slightly, in a magnitude smaller than each of major uncertainties from the drifts by at least 1 order; however, it eliminates the need for ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}$ in the CO₂ accuracy Eq. (14) and for ${\mathit{\rho }}_{{\mathrm{CO}}_{\mathrm{2}}}$ in the H₂O accuracy Eq. (22), which makes the equations easily applicable.

Precision uncertainty is statistically formulated as Eq. (4) for CO₂ and Eq. (16) for H₂O. This formulation is common practice based on statistical methods (Hoel, 1984).

7.3 Use of relative accuracy for infrared analyzer specifications

Relative accuracy is often used concurrently with accuracy to specify sensor measurement performance. The accuracy is the numerator of relative accuracy whose denominator is the true value of a measured variable. When evaluated for the applications of OPEC systems in ecosystems, CO₂ accuracy in magnitude is small in a range within 1 order (0.39–1.22 mgCO₂ m⁻³, data for Fig. 2a), and so is H₂O accuracy (0.04–0.10 gH₂O m⁻³, data for Fig. 3a). In ecosystems, CO₂ is naturally high, as compared to its accuracy magnitude, and does not change much in terms of a magnitude order (e.g., no more than 1 order from 600 to 1600 mgCO₂ m⁻³, assumed in this study). However, unlike CO₂, H₂O naturally changes dramatically in its amount across at least 3 orders in magnitude (e.g., at 101.325 kPa, from 0.03 gH₂O m⁻³ when RH is 10 % at −30 ^∘C to 40 gH₂O m⁻³ when dew point temperature is 35 ^∘C at the highest as reported by the National Weather Service, 2022; under drier conditions, the H₂O amount could be even lower). Because, in ecosystems, CO₂ changes differently from H₂O in amount across magnitude orders, the relative accuracy behaviors in CO₂ differ from H₂O (Figs. 2b and 3b).

7.3.1 CO₂ relative accuracy

Because of the small CO₂ accuracy magnitude relative to the natural CO₂ amount in ecosystems, the CO₂ relative accuracy magnitude varies within a narrow range of ±0.07 to ±0.19 % (Sect. 4.5.2). If the relative accuracy is used, either a range of ±0.07 to ±0.19 % or an inequality of ≤ 0.19 % in magnitude can be specified as the CO₂ relative accuracy for field CO₂ measurements. Both range and inequality would be equivalently perceived by users to be a fair performance of the infrared analyzers in OPEC systems. For simplicity, our study specifies the CO₂ relative accuracy for the EC150 infrared analyzers to be ±0.19 % after a manufacturing calibration (data shown in Fig. 2b).

7.3.2 H₂O relative accuracy

Although the H₂O accuracy magnitude is also small, the “relatively” great change in natural-air H₂O across several magnitude orders in ecosystems results in a much wider range of the H₂O relative accuracy magnitude, from ±0.23 % at maximum air moisture to ±96 % when RH is 20 % at −30 ^∘C (Fig. 3b and Sect. 5.4.2). H₂O relative accuracy can be much greater under dry conditions at low T_a (e.g., ±192 % for air when RH is 10 % at −30 ^∘C). Accordingly, if the relative accuracy is used, either a range of ±0.23 % to ±192 % or an inequality of ≤ 192 % in magnitude can be specified as the H₂O relative accuracy for field H₂O measurements. Either the range or the inequality could be perceived by users intrinsically as a poor measurement performance of the infrared analyzers in OPEC systems, although either specification is conditionally right for fair H₂O measurement.

Apparently, the relative accuracy for H₂O measurements in ecosystems is not intrinsically interpretable by users to correctly perceive the performance of the infrared analyzers in OPEC systems. Instead, if H₂O relative accuracy is unconditionally specified just in an inequality of ≤ 192 % in magnitude, it could easily mislead users to wrongly assess the performance as unacceptable for H₂O measurements, although this performance of the infrared analyzers in OPEC systems is fair for air when RH is 10 % at −30 ^∘C. Therefore, H₂O relative accuracy is not recommended to be used for specification of infrared analyzers for H₂O measurement performance. If this descriptor is used, the H₂O relative accuracy under a standard condition should be specified. This condition may be defined as saturated air at 35 ^∘C (i.e., the highest natural dew point; National Weather Service, 2022) under normal P of 101.325 kPa (Wright et al., 2003). For our case study, under such a standard condition, the H₂O relative accuracy can be specified within ±0.18 % after a manufacturing calibration (data for Fig. 3b).

8 Conclusions

The accuracy of field ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ measurements from the infrared analyzers in OPEC systems can be defined as a maximum range of composited measurement uncertainty (Eqs. 14 and 22) from the specified sources: zero drift, gain drift, sensitivity to ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$, and precision variability (Table 1), all of which are included in the system specifications for infrared CO₂–H₂O analyzers currently used in field OPEC systems. The specified uncertainties interactionally or independently contribute to the overall uncertainty. Fortunately, the interactions between component uncertainties in each pair is 3 orders smaller than either component individually (Appendix A). Therefore, these specified uncertainties can be simply added together as the accuracy range in a general ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ accuracy model for the infrared analyzers in OPEC systems (Model 2). Based on statistics, bio-environment, and approximation, the specification descriptors of the infrared analyzers in OPEC systems are incorporated into the model terms to formulate the CO₂ accuracy Eq. (14) and the H₂O accuracy Eq. (22), both of which are computable to evaluate corresponding CO₂ and H₂O accuracies. For the EC150 infrared analyzers used in the OPEC systems over their operational range in T_a at the standard P of 101.325 kPa (Figs. 2 and 3 and Table 2), the CO₂ accuracy can be specified as ±1.22 mgCO₂ m⁻³ (relatively within ±0.19 %, Fig. 2) and H₂O accuracy as ±0.10 gH₂O m⁻³ (relatively within ±0.18 % for saturated air at 35 ^∘C at the standard P, Fig. 3).

Both accuracy equations are not only applicable for further uncertainty estimation for CO₂ and H₂O fluxes due to CO₂ and H₂O measurement uncertainties (Eqs. 27 and 28) and the error/uncertainty analyses in CO₂ and H₂O data applications (e.g., Eq. 29); they may also be used as a rationale to assess and guide field maintenance on infrared analyzers. Equation (14) as shown in Fig. 2a, along with Eqs. (7) and (11) as shown in Fig. 4a, guides users to adjust the CO₂ zero and CO₂ gain drifts, through the corresponding zero and span procedures, near a T_a value that minimizes the T_a departures, on average, during the period of interest if this period were not under extreme and hazard conditions (Fratini et al., 2014). As assessed on atmospheric CO₂ background, the procedures can narrow the maximum CO₂ accuracy range by 40 %, from ±1.22 to ±0.72 mgCO₂ m⁻³ and thereby greatly improve the CO₂ measurement accuracies with these regular zero and span procedures for CO₂.

Equation (22) as shown in Fig. 3a, along with Eqs. (18) and (19) as shown in Fig. 4b, presents users with a rationale to adjust the H₂O zero drift of infrared analyzers in the same technique as for CO₂, but the H₂O gain drift under hot and humid environments needs more attention (see the right portion above T_c in Figs. 3a and 4b); under cold and/or dry environments, it does not merit further concern (see the left portion below 0 ^∘C in Fig. 4b). In a T_a range above 5 ^∘C, the maximum H₂O accuracy range of ±0.10 gH₂O m⁻³ can be narrowed by 30 % to ±0.07 gH₂O m⁻³ if both zero and span procedures for H₂O are performed as necessary. In a T_a range below 5 ^∘C, the H₂O zero procedure alone can narrow the maximum H₂O accuracy range of ±0.066 gH₂O m⁻³ by 22 % to ±0.051 gH₂O m⁻³. Under cold environmental conditions, the H₂O span procedure is found to be unnecessary (Fig. 5), and the H₂O zero procedure is proposed as the only, and prominently efficient, option to minimize H₂O measurement uncertainty from the infrared analyzers in OPEC systems. This procedure plays the same role under dry conditions. Under cold and/or dry environments, the zero procedure for CO₂ and H₂O together would be a practical and efficient option not only to warrant but also to improve measurement accuracy. In a cold environment, adjusting the H₂O gain drift is impractical because of the failure of a dew point generator under freezing conditions.

Additionally, as a specification descriptor for OPEC systems used in ecosystems, relative accuracy is applicable for CO₂ instead of H₂O measurements. A small range in the CO₂ relative accuracy can be perceived intuitively by users as normal. In contrast, without specifying the condition of air moisture, a large range in H₂O relative accuracy under cold and/or dry conditions (e.g., 100 %) can easily mislead users to an incorrect conclusion in interpretation of H₂O measurement reliability, although it is the best achievement of the modern infrared analyzers under such conditions. If the H₂O relative accuracy is used, the authors suggest conditionally defining it for saturated air at 35 ^∘C (i.e., 39.66 gH₂O m⁻³ at 101.352 kPa). Ultimately, this study provides some scientific bases for the flux community to specify the accuracy of CO₂–H₂O measurements from the infrared analyzers in OPEC systems, although only one model of infrared analyzers (i.e., EC150) is used for this study.

Appendix A: Derivation of the accuracy model for infrared CO₂–H₂O analyzers

As defined in the Introduction, the measurement accuracy of infrared CO₂–H₂O analyzers is a range of the difference between the true α density (ρ_αT, where α can be either CO₂ or H₂O) and α density (ρ_α) measured by the analyzers. The difference is denoted by Δρ_α, given by Eq. (1) in Sect. 3. The range of this difference is contributed from the analyzer performance uncertainties, as specified by the use of the four descriptors: zero drift, gain drift, cross-sensitivity, and precision (LI-COR Biosciences, 2021c; Campbell Scientific Inc., 2021b).

According to the definitions in Sect. 2, zero drift uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}$) is independent of ρ_αT value and gain trend related to analyzer response; so, too, is cross-sensitivity uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}$), which depends upon the amount of background H₂O in the measured air if α is CO₂ and upon the amount of background CO₂ in the measured air if α is H₂O. In the case that both gain drift and precision uncertainties are zero, $\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}$ and $\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}$ are simply additive to any true value as a measured value, including zero drift and cross-sensitivity uncertainties (ρ_{α_zs}):

$$\begin{array}{}\text{(A1)}& {\mathit{\rho }}_{\mathit{\alpha }\mathit{\_}\mathrm{zs}}={\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}},\end{array}$$

where subscript z indicates zero drift uncertainty included in the measured value and subscript s indicates cross-sensitivity uncertainty included in the measured value. During the measurement process, while zero is drifting and cross-sensitivity is active, if gain also drifts, then the gain drift interacts with the zero drift and the cross-sensitivity. This is because ρ_{α_zs} is a linear factor for this gain drift (see the cells along the gain drift row in the value columns in Table 1) that is added to ρ_{α_zs} as a measured value additionally including gain drift uncertainty (ρ_{α_zsg}, where subscript g indicates gain drift uncertainty included in the measured value), given by

$$\begin{array}{}\text{(A2)}& {\displaystyle }{\mathit{\rho }}_{\mathit{\alpha }\mathit{\_}\mathrm{zsg}}={\mathit{\rho }}_{\mathit{\alpha }\mathit{\_}\mathrm{zs}}+{\mathit{\delta }}_{\mathit{\alpha }\mathit{\_}\mathrm{g}}{\mathit{\rho }}_{\mathit{\alpha }\mathit{\_}\mathrm{zs}},\end{array}$$

where δ_{α_g} is gain drift percentage (e.g., in the case of this study, ${\mathit{\delta }}_{{\mathrm{CO}}_{\mathrm{2}}\mathit{\_}\mathrm{g}}=\mathrm{0.10}$ % and ${\mathit{\delta }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}\mathit{\_}\mathrm{g}}=\mathrm{0.30}$ %, Table 1). Substituting ρ_{α_zs}, as expressed in Eq. (A1), into this equation leads to

$$\begin{array}{}\text{(A3)}& \begin{array}{rl}{\mathit{\rho }}_{\mathit{\alpha }\mathit{\_}\mathrm{zsg}}& ={\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}+{\mathit{\delta }}_{\mathit{\alpha }\mathit{\_}\mathrm{g}}{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}\\ & +{\mathit{\delta }}_{\mathit{\alpha }\mathit{\_}\mathrm{g}}\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}+{\mathit{\delta }}_{\mathit{\alpha }\mathit{\_}\mathrm{g}}\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}.\end{array}\end{array}$$

In this equation, ${\mathit{\delta }}_{\mathit{\alpha }\mathit{\_}g}\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}$ is the zero–gain interaction and ${\mathit{\delta }}_{\mathit{\alpha }\mathit{\_}\mathrm{g}}\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}$ is the cross-sensitivity–gain interaction. In magnitude, the former is 3 orders smaller than either zero drift uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}$) or gain drift uncertainty (δ_{α_g}ρ_αT), and the latter is 3 orders smaller than either cross-sensitivity uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}$) or gain drift uncertainty. Therefore, both interactions are relatively small and can be reasonably dropped. As a result, Eq. (A3) can be approximated and rearranged as

$$\begin{array}{}\text{(A4)}& \begin{array}{rl}{\mathit{\rho }}_{\mathit{\alpha }\mathit{\_}\mathrm{zsg}}& \approx {\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}+{\mathit{\delta }}_{\mathit{\alpha }\mathit{\_}\mathrm{g}}{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}\\ & ={\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{g}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}},\end{array}\end{array}$$

where $\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{g}}$ is a gain drift uncertainty. Any measured value has a random error (i.e., precision uncertainty) independent of ρ_αT in value (ISO, 2012). Therefore, ρ_{α_zsg} plus precision uncertainty ($\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{p}}$) is the measured value including all uncertainties (ρ_α), given by

$$\begin{array}{}\text{(A5)}& {\mathit{\rho }}_{\mathit{\alpha }}={\mathit{\rho }}_{\mathit{\alpha }\mathit{\_}\mathrm{zsg}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{p}}.\end{array}$$

The insertion of Eq. (A4) into this equation leads to

$$\begin{array}{}\text{(A6)}& {\mathit{\rho }}_{\mathit{\alpha }}-{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}=\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{g}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{p}}.\end{array}$$

This equation holds true for

$$\begin{array}{}\text{(A7)}& \mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}\le \left|\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{z}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{g}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{s}}\right|+\left|\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}^{\mathrm{p}}\right|.\end{array}$$

The range of the right side of this equation is wider than the measurement uncertainty from all measurement uncertainty sources, as shown on the right side of Eq. (A6), and the difference of ρ_α minus ρ_αT (i.e., Δρ_α). Using this range, the measurement accuracy is defined in Model (2) in Sect. 3.

Appendix B: Water vapor density from ambient air temperature, relative humidity, and atmospheric pressure

Given ambient air temperature (T_a in ^∘C) and atmospheric pressure (P in kPa), air has a limited capacity to hold an amount of water vapor (Wallace and Hobbs, 2006). This limited capacity is described in terms of saturation water vapor density (ρ_s in gH₂O m⁻³) for moist air, given through the Clausius–Clapeyron equation (Sonntag, 1990; Wallace and Hobbs, 2006):

$$\begin{array}{}\text{(B1)}& \begin{array}{rl}& {\mathit{\rho }}_{\mathrm{s}}\left(T_{\mathrm{a}},P\right)=\\ & {\displaystyle \frac{\mathrm{0.6112}f\left(P\right)}{R_{\mathrm{v}}(\mathrm{273.15}+T_{\mathrm{a}})}}\left\{\begin{array}{ll}\exp \left(\frac{\mathrm{17.62}{T}_{\mathrm{a}}}{T_{\mathrm{a}}+\mathrm{243.12}}\right)& T_{\mathrm{a}}\ge \mathrm{0}\\ & \\ \exp \left(\frac{\mathrm{22.46}{T}_{\mathrm{a}}}{T_{\mathrm{a}}+\mathrm{272.62}}\right)& T_{\mathrm{a}}<\mathrm{0},\end{array}\right.\end{array}\end{array}$$

where R_v is the gas constant for water vapor ($\mathrm{4.61495}\times {\mathrm{10}}^{-\mathrm{4}}$ kPa m³ K⁻¹ gH₂O⁻¹) and f(P) is an enhancement factor for moist air, being a function of P as $f\left(P\right)=\mathrm{1.0016}+\mathrm{3.15}\times {\mathrm{10}}^{-\mathrm{5}}P-\mathrm{0.0074}{P}^{-\mathrm{1}}$. At relative humidity (RH in %), the water vapor density [${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{RH}}\left(T_{\mathrm{a}},P\right)$ in gH₂O m⁻³] is

$$\begin{array}{}\text{(B2)}& {\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{RH}}\left(T_{\mathrm{a}},P\right)=\mathrm{RH}{\mathit{\rho }}_{\mathrm{s}}\left(T_{\mathrm{a}},P\right).\end{array}$$

This equation, along with Eq. (B1), is used to calculate ${\mathit{\rho }}_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}^{\mathrm{RH}}$ used in Fig. 3 in Sect. 5.4 and Figs. 4b and 5 in Sect. 6.3.

Appendix C: The relationship of measured to true covariance of vertical wind speed with CO₂, H₂O, or air temperature

For open-path eddy-covariance systems, the computation of ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ flux between ecosystems and the atmosphere starts from covariance of an individual 3-D wind component with a ${\mathrm{CO}}_{\mathrm{2}}/{\mathrm{H}}_{\mathrm{2}}\mathrm{O}$ density. To express the covariance, as similarly used in Eqs. (1), α is used as a subscript of ρ to represent either CO₂ or H₂O and subscript T is used to indicate a measurement free of uncertainty as if it were true. According to Eq. (1), a measured α density (ρ_α) with a measurement uncertainty (Δρ_α) can be expressed as

$$\begin{array}{}\text{(C1)}& {\mathit{\rho }}_{\mathit{\alpha }}={\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }},\end{array}$$

where ρ_αT is an assumed α density free of measurement uncertainty as if measured by an accurate sensor with the same frequency response as the one measuring ρ_α. This assumed α density (ρ_αT) is also referred to as “true α density” although it is not. The covariance of vertical wind speed (w) with ρ_α is given by

$$\begin{array}{}\text{(C2)}& \stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }}={\displaystyle \frac{\mathrm{1}}{n}}{\sum }_{i=\mathrm{1}}^n\left(w_i-\stackrel{\mathrm{‾}}{w}\right)\left({\mathit{\rho }}_{\mathit{\alpha }i}-{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathit{\alpha }}\right),\end{array}$$

where n is the sample number over an averaging interval (e.g., 36 000 over a 1 h interval if w_i and ρ_αi are measured at 10 Hz), subscript i indexes the sequential numbers for w_i and ρ_αi, the overbar is the Reynolds' averaging operator, and prime denotes the fluctuation in a variable away from its mean (e.g., $w_i^{\prime }=w_i-\stackrel{\mathrm{‾}}{w}$). Without considering the measurement error of w for this study topic, submitting Eq. (C1) into Eq. (C2) leads to

$$\begin{array}{}\text{(C3)}& \begin{array}{rl}\stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }}& ={\displaystyle \frac{\mathrm{1}}{n}}{\sum }_{i=\mathrm{1}}^n\left(w_i-\stackrel{\mathrm{‾}}{w}\right)[{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}i}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }i}\\ & -\stackrel{\mathrm{‾}}{\left({\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}+\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }}\right)}]\\ & ={\displaystyle \frac{\mathrm{1}}{n}}{\sum }_{i=\mathrm{1}}^n\left(w_i-\stackrel{\mathrm{‾}}{w}\right)\left({\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}i}-{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathit{\alpha }\mathrm{T}}\right)\\ & +{\displaystyle \frac{\mathrm{1}}{n}}{\sum }_{i=\mathrm{1}}^n\left(w_i-\stackrel{\mathrm{‾}}{w}\right)\left(\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }i}-\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathit{\alpha }}\right).\end{array}\end{array}$$

Within an averaging interval (e.g., 1 h), the systematic error components inside terms Δρ_αi and $\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathit{\alpha }}$ are not only constant but also equal. Accordingly, the systematic errors inside the term $\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }i}-\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathit{\alpha }}$ are canceled out (Richardson et al., 2012). In essence, this term is a random error whose statistical distribution is generally assumed to be normal with a zero mean (i.e., $\mathrm{\Delta }{\mathit{\rho }}_{\mathit{\alpha }i}-\mathrm{\Delta }{\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathit{\alpha }}$ is expected to be zero; Hoel, 1984). The correlation of w with a random variable normally distributed with an expected zero mean tends to be zero, particularly for a large sample of 36 000 under discussion, even 18 000 for half hours (Snedecor and Cochran, 1989), which is the shortest period commonly used for flux computations. Accordingly, the term in the fourth line of Eq. (C3) can be regarded as zero. Therefore, the covariance of w with measured α density is equal to the covariance of w with the true α density, given by

$$\begin{array}{}\text{(C4)}& \stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }}=\stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}^{\prime }}.\end{array}$$

If w from a sonic anemometer and ρ_α from an infrared analyzer are not measured through spatial and temporal synchronization, the values of covariance of w with ρ_α in the different lags of measurement (hereafter referred to as the lagged covariance) are computed for use in the lag maximization to find their maximum covariance as if w and ρ_α were measured at the same time in the same space (Moncrieff et al., 1997; Ibrom et al., 2007). Each lagged covariance from field measurements can be expressed as $\stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$, where subscript l is the index for a lag number. If l=i, w_i and ρ_αl were measured at the same time. If $l=i-\mathrm{1}$, w_i was measured one measurement interval (i.e., 100 ms for 10 Hz measurements) later than ρ_αl, whereas w_i was measured one measurement interval earlier than ρ_αl if $l=i+\mathrm{1}$. The index l can be −k to k where k is a positive integer, including 0, to represent the maximum number of the lags that is optional to users. Therefore, given l from −k to k, the number of $\stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$ values is 2k+1. Using the same approach to Eq. (C4), $\stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}=\stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}l}^{\prime }}$ can be proved.

The lagged covariance values for $\stackrel{\mathrm{‾}}{u^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$ and $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$ (l is −k, $-k+\mathrm{1}$, …, 0, …, or k) are also computed for each lag where, in the sonic anemometer coordinate system, u is the wind speed in the x direction and v is the wind speed in the y direction. Both $\stackrel{\mathrm{‾}}{u^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}=\stackrel{\mathrm{‾}}{u^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}l}^{\prime }}$ and $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}=\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}l}^{\prime }}$ can also be proved in the same way for Eq. (C4). Given the rotation angles from $\stackrel{\mathrm{‾}}{u}$, $\stackrel{\mathrm{‾}}{v}$, $\stackrel{\mathrm{‾}}{w}$, $\stackrel{\mathrm{‾}}{u^{\mathrm{2}}}$, $\stackrel{\mathrm{‾}}{v^{\mathrm{2}}}$, $\stackrel{\mathrm{‾}}{w^{\mathrm{2}}}$, $\stackrel{\mathrm{‾}}{u^{\prime }{v}^{\prime }}$, $\stackrel{\mathrm{‾}}{u^{\prime }{w}^{\prime }}$, and $\stackrel{\mathrm{‾}}{v^{\prime }{w}^{\prime }}$ (Tanner and Thurtell, 1969), each set of $\stackrel{\mathrm{‾}}{u^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$, $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$, and $\stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$ is rotated to be ${\stackrel{\mathrm{‾}}{\left(u^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }\right)}}_{\mathrm{r}}$, ${\stackrel{\mathrm{‾}}{\left(v^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }\right)}}_{\mathrm{r}}$, and ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }\right)}}_{\mathrm{r}}$, respectively, where u, v, and w through the rotations are transformed into the natural wind coordinate system correspondingly as stream-wise, lateral, and vertical wind speeds. In the rotation process, ρ_α is not additionally involved. Because ${\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }$ inside the covariance is a scalar rather than a vector variable, the rotation would not be influenced by ${\stackrel{\mathrm{‾}}{\mathit{\rho }}}_{\mathit{\alpha }l}$ and $\stackrel{\mathrm{‾}}{{\mathit{\rho }}_{\mathit{\alpha }l}^{\mathrm{2}}}$ in the same way as by the three means and three variance values of 3-D wind components (Tanner and Thurtell, 1969). Because the same set of rotation angles also should be used for the rotations of $\stackrel{\mathrm{‾}}{u^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}l}^{\prime }},\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}l}^{\prime }}$, and $\stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}l}^{\prime }}$, the covariance values rotated from these three covariance values are correspondingly equal to those rotated from $\stackrel{\mathrm{‾}}{u^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$, $\stackrel{\mathrm{‾}}{v^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$, and $\stackrel{\mathrm{‾}}{w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }}$, for the covariance values related to w, given by

$$\begin{array}{}\text{(C5)}& {\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }\right)}}_{\mathrm{r}}={\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}l}^{\prime }\right)}}_{\mathrm{r}}.\end{array}$$

Therefore, from the lag maximization (Moncrieff et al., 1997; Ibrom et al., 2007), the maximum covariance in magnitude among ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }l}^{\prime }\right)}}_{\mathrm{r}}$ (l from −k to k) is equal to the maximum in magnitude among ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}l}^{\prime }\right)}}_{\mathrm{r}}$. Denoting the former maximum covariance by ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }\right)}}_{\mathrm{rm}}$, where subscript m indicates the lag maximization, and the latter one by ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}^{\prime }\right)}}_{\mathrm{rm}}$, this equality leads to

$$\begin{array}{}\text{(C6)}& {\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }\right)}}_{\mathrm{rm}}={\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}^{\prime }\right)}}_{\mathrm{rm}}.\end{array}$$

For flux computations, both covariance values in this equation need further corrections for their low- and high-frequency loss (Moore, 1986). The correction factor for ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }\right)}}_{\mathrm{rm}}$ can be denoted by f_cα and for ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}^{\prime }\right)}}_{\mathrm{rm}}$ can be denoted by f_cαT. Both f_cα and f_cαT are integrated in the same way from the cospectrum of w with a scalar as represented by T_a (air temperature) and the transfer functions of high-frequency loss separately for w and α density (Moore, 1986; van Dijk, 2002) and low-frequency loss for Reynolds' averaging $w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }$ (Massman, 2000). Although depending on the structure of boundary-layer turbulent flows (Kaimal and Finnigan, 1994), under the same boundary-layer turbulent flows, the cospectrum for w with ρ_α is the same as for w with ρ_αT. Because the sensor for ρ_αT is assumed to have the same frequency response as the sensor for ρ_α, both sensors have the same high-frequency loss, sharing the same transfer function (Moore, 1986). The transfer function for low-frequency loss due to Reynolds' averaging either side of Eq. (C6) is also used for its other side (Massman, 2000). Therefore, f_cα is equal to f_cαT, which, from Eq. (C6), leads to

$$\begin{array}{}\text{(C7)}& f_{\mathrm{c}\mathit{\alpha }}{\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }\right)}}_{\mathrm{rm}}=f_{\mathrm{c}\mathit{\alpha }\mathrm{T}}{\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}^{\prime }\right)}}_{\mathrm{rm}}.\end{array}$$

In this equation, the left term is the frequency-corrected ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }\right)}}_{\mathrm{rm}}$, which can be denoted by ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }\right)}}_{\mathrm{rmf}}$ where subscript f indicates this covariance to be corrected for frequency loss, and the right term is the frequency-corrected ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}^{\prime }\right)}}_{\mathrm{rm}}$, which can be denoted by ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}^{\prime }\right)}}_{\mathrm{rmf}}$ (Moore, 1986; Massman, 2000; van Dijk, 2002). Accordingly, Eq. (C7) becomes

$$\begin{array}{}\text{(C8)}& {\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }\right)}}_{\mathrm{rmf}}={\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}^{\prime }\right)}}_{\mathrm{rmf}},\end{array}$$

where subscript rmf indicates the covariance was corrected through coordinate rotations (r), lag maximization (m), and low- and high-frequency corrections (f). Equation (C8) shows the covariance of w with measured ρ_α is equal to its counterpart of w with true ρ_α even after a series of corrections before being used to calculate α flux through Webb–Pearman–Leuning (WPL) corrections (Webb et al., 1980).

For the covariance of w with T_a, the same conclusion can be derived, given by

$$\begin{array}{}\text{(C9)}& {\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{a}}^{\prime }\right)}}_{\mathrm{rmf}}={\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathrm{aT}}^{\prime }\right)}}_{\mathrm{rmf}}.\end{array}$$

Assuming w to be an accurate value for this study topic, through WPL corrections, ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }}^{\prime }\right)}}_{\mathrm{rmf}}$ and ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathit{\alpha }}^{\prime }\right)}}_{\mathrm{rmf}}$ can be used to derive an analytical equation for a measured α flux from ρ_α and T_a, each of which includes a measurement error, whereas ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{\mathit{\rho }}_{\mathit{\alpha }\mathrm{T}}^{\prime }\right)}}_{\mathrm{rmf}}$ and ${\stackrel{\mathrm{‾}}{\left(w^{\prime }{T}_{\mathit{\alpha }\mathrm{T}}^{\prime }\right)}}_{\mathrm{rmf}}$ can be used to derive an analytical equation for a true α flux from ρ_αT and T_aT, each of which is assumed not to include an error. The comparison of both analytical equations can demonstrate the partial effects of Δρ_α on the uncertainty in α flux data (see Sect. 6.1).