Tri-axial square Helmholtz coil system at the Alibag Magnetic Observatory: upgraded to a magnetic sensor calibration facility

A tri-axial square Helmholtz coil system for the study of palaeomagnetic studies, manufactured by GEOFYZIKA (former Czechoslovakia), was successfully commissioned at the Alibag Magnetic Observatory (IAGA code: ABG) in the year 1985. This system was used for a few years, after which the system encountered technical problems with the control unit. Rectification of the unit could not be undertaken, as the information document related to this system was not available, and as a result the system had been lying in an unused state for a long time, until 2015, when the system was recommissioned and upgraded to a test facility for calibrating the magnetometer sensors. We have upgraded the system with a constant current source and a data-logging unit. Both of these units have been designed and developed in the institute laboratory. Also, re-measurements of the existing system have been made thoroughly. The upgraded system is semi-automatic, enabling non-specialists to operate it after a brief period of instruction. This facility is now widely used at the parent institute and external institutions to calibrate magnetometers and it also serves as a national facility. Here the design of this system with the calibration results for the space-borne fluxgate magnetometers is presented.

1 Introduction

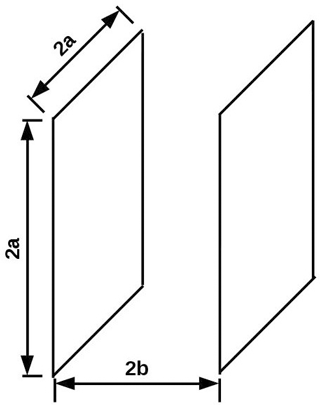
The Helmholtz coil system, which is a useful in laboratory techniques, is normally used to generate magnetic field levels of specified volume and uniformity. These coils provide accurate means to perform numerous experiments and testing functions that require a known ambient magnetic field. The field generation can be either static, time-varying direct current or alternating current depending on the applications requirements. Typical applications include magnetometer calibration, magnetic compass calibration, satellite characterization and biomagnetic studies (Herceg et al., 2009). Square Helmholtz coils can be utilized instead of circular Helmholtz coils in the design, as they provide a wider uniform field of ≈ 5 L parallel to the coils compared to circular coils. The governing equation for the magnetic field B at the centre point of a square coil pair is

$$\begin{array}{}\text{(1)}& {\displaystyle }B={\displaystyle \frac{\mathrm{2}{\mathit{\mu }}_{\mathrm{0}}NI}{\mathit{\pi }a}}{\displaystyle \frac{\mathrm{2}}{(\mathrm{1}+{\mathit{\gamma }}^{\mathrm{2}})\sqrt{\mathrm{2}+{\mathit{\gamma }}^{\mathrm{2}}}}},\end{array}$$

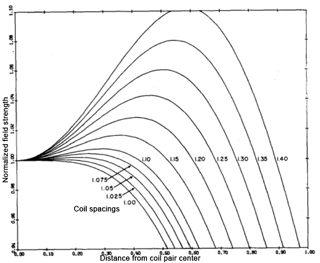
where μ₀ is the permeability of the vacuum, $\mathrm{4}\mathit{\pi }\times {\mathrm{10}}^{-\mathrm{7}}$ N A⁻²; N is the number of wrappings; I is the current passing through the coils; a is half the length of a side of the coil; and γ is the ratio of the distance between the two coils 2b and the length of the side of a coil 2a as shown in Fig. 1. In order to achieve a homogeneous field at the mid-point of the square Helmholtz coil pair, γ is 0.5445, which is a Helmholtz spacing ratio. Equation (1) relies on the coils being orthogonal, centred and properly spaced. “If the coils are not properly spaced, a profile similar to that of Fig. 2 is achieved” (Brewer, 2012).

Figure 1 Square Helmholtz coil pair.

Figure 2 Magnetic field uniformity for a circular coil (Rudd and Craig, 1968).

The square Helmholtz coil utilizes two pairs of square Helmholtz coils or three orthogonal pairs of Helmholtz coils which permit 3-axis control of a magnetic field within the coils. This configuration of three orthogonal square coil pairs is often referred to as a “Helmholtz cage”. Commercial cages are manufactured by Bartington Instruments Limited (Bartington), Serviciencia and Macintyre Electronic Design Associates, Inc. (MEDA). Several universities have built Helmholtz cages to develop and test sensors for space applications. Also, the Naval Post Graduate School (NPS) in Monterrey, CA, the University of Michigan (U-M) in Ann Arbor, MI (Klesh et al., 2010) and the Delft University of Technology in the Netherlands (Poppenk et al., 2006, 2007) have all built Helmholtz cages (Brewer, 2012).

One such Helmholtz cage for the study of palaeomagnetic studies was commissioned at the Alibag Magnetic Observatory in the year 1985. After a few years of operation this system encountered technical problems associated with the feedback mechanism of the closed-loop system and had to be abandoned. This being a square Helmholtz coil system, we realized its importance for calibrating ground and space based magnetometer sensors, and with this purpose the system was redesigned by introducing a constant current source (CCS) and a data logger. Also, all the technical parameters of the system were recalculated (Table 1). This compact unit is now referred to as the tri-axial square Helmholtz coil system. This system generates uniform, accurate and precise magnetic fields in a volume of ≈ 5 L (considering a cubic sensor of 17 cm³), which is accurate to 1 nT about the centre of the coil system and serves as a calibration facility for both space- and ground-borne magnetometer sensors. The schematic of the system is shown in Fig. 3.

Table 1 Coil specifications.

Figure 3 Schematic of the redesigned Helmholtz coil calibration facility.

2 Description of the tri-axial square Helmholtz coil system

The tri-axial square Helmholtz coil system (cage) is a three-component device that uses three pairs of square field coils to produce a homogeneous magnetic field in the working space at the centre of the system. The individual coil pairs are spaced to fulfil the familiar Helmholtz condition that the second-order derivative of the field produced along the axis of the coil pairs is zero at the pair centre.

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{d^{\mathrm{2}}\mathrm{B}}{\mathrm{d}{x}^{\mathrm{2}}}}={\displaystyle \frac{N{\mathit{\mu }}_{\mathrm{o}}i{R}^{\mathrm{2}}}{\mathrm{2}}}\left[-{\displaystyle \frac{\mathrm{3}}{{\left(R^{\mathrm{2}}+x^{\mathrm{2}}\right)}^{\mathrm{5}/\mathrm{2}}}}+{\displaystyle \frac{\mathrm{15}{x}^{\mathrm{2}}}{{\left(R^{\mathrm{2}}+x^{\mathrm{2}}\right)}^{\mathrm{7}/\mathrm{2}}}}\right.\\ {\displaystyle }& {\displaystyle }\left.-{\displaystyle \frac{\mathrm{3}}{{\left(R^{\mathrm{2}}+x^{\mathrm{2}}-\mathrm{2}sx+s^{\mathrm{2}}\right)}^{\mathrm{5}/\mathrm{2}}}}+{\displaystyle \frac{\mathrm{15}(x-s{)}^{\mathrm{2}}}{{\left(R^{\mathrm{2}}+x^{\mathrm{2}}-\mathrm{2}sx+s^{\mathrm{2}}\right)}^{\mathrm{7}/\mathrm{2}}}}\right]\end{array}$$

At $x=s/\mathrm{2}$

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{d^{\mathrm{2}}\mathrm{B}}{\mathrm{d}{x}^{\mathrm{2}}}}{\mathrm{|}}_{s/\mathrm{2}}={\displaystyle \frac{N{\mathit{\mu }}_{\mathrm{o}}i{R}^{\mathrm{2}}}{\mathrm{2}}}\left[-{\displaystyle \frac{\mathrm{6}}{{\left(R^{\mathrm{2}}+s^{\mathrm{2}}/\mathrm{4}\right)}^{\mathrm{5}/\mathrm{2}}}}+{\displaystyle \frac{\mathrm{30}{s}^{\mathrm{2}}/\mathrm{4}}{{\left(R^{\mathrm{2}}+s^{\mathrm{2}}/\mathrm{4}\right)}^{\mathrm{7}/\mathrm{2}}}}\right]\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{N{\mathit{\mu }}_{\mathrm{o}}i{R}^{\mathrm{2}}}{\mathrm{2}}}\left[{\displaystyle \frac{-\mathrm{6}\left(R^{\mathrm{2}}+s^{\mathrm{2}}/\mathrm{4}\right)+\mathrm{30}{s}^{\mathrm{2}}/\mathrm{4}}{{\left(R^{\mathrm{2}}+s^{\mathrm{2}}/\mathrm{4}\right)}^{\mathrm{7}/\mathrm{2}}}}\right]\\ {\displaystyle }& {\displaystyle }=\mathrm{3}N{\mathit{\mu }}_{\mathrm{o}}i{R}^{\mathrm{2}}{\displaystyle \frac{s^{\mathrm{2}}-R^{\mathrm{2}}}{{\left(R^{\mathrm{2}}+s^{\mathrm{2}}/\mathrm{4}\right)}^{\mathrm{7}/\mathrm{2}}}}\end{array}$$

Clearly, this is zero if s=R.

This appropriate spacing of the square field coils is 0.5445 at the side of the square. These dimensions provide optimal uniformity over a region. This system yields a working-space volume of approx. 5 L (considering a cubic sensor of 17 cm³) with a maximum of ±2 nT of the added field homogeneity deviation and is realized by using the square-shaped coils of 2–2.5 m in size. The coils are supported by a borosilicate glass piping construction to electrically isolate the coils from the support structure (Fig. 7). The primary glass support structure at the end corners is joined using a female square-design six-way cross aluminium connector, to which a Bakelite bracket is fixed using a nut and bolt. Borosilicate glass is selectively chosen as it possess outstanding corrosion resistance and low coefficients of thermal expansion. The piping appears clear and colourless as borosilicate glass shows no appreciable absorption in the visible region of the spectrum. The coefficient of thermal expansion of aluminium (Hidnert, 2018) is greater than that of borosilicate glass. As a result the corners remain intact for years. The Bakelite bracket is a rounded triangle quarter and the radii of the quarters are 149.86 and 124 mm. This bracket is used for rolling the coil at the edges and ensures additional stiffness. Additional strength is provided to the primary glass assembly by implementing a triangular-structure design where the apex of the triangle joins the corners and the three corners of the base meet the adjacent sides of the primary glass frame (Fig. 4). Also, thin Bakelite blocks have been fixed to the support frame using a strong adhesive to hold the coils (Fig. 6). These serve as an intermediary between the coil and the support frame and are uniformly spaced all along the length of the frame. This construction design yields a cage that ensures stability of the system geometry independent of the environmental parameters and time. The diameter of the primary glass tube is 172 mm and for the glass tube implemented in the triangular structure it is 146 mm. The surface area of the aluminium connector is 2053.5 cm². Bakelite is used for its electrical non-conductive and heat-resistant properties.

Figure 4 Triangular structure design ensures additional stiffness at the corners of the cage.

The coils consist of 12 AWG copper wires wound to attain the shape of a cuboid. The wind is parallel to the length of the cuboid. The thickness of the wire is 127 mm. The wires are laid in neat rows so that the magnetic field is completely perpendicular to the flow of the current. There are two electrically isolated wires in each coil. However the number of turns was not known. The final coil is wrapped with insulation of 0.7 mm thickness. The outermost coil is a pair of wires and is a perfect square with an area 62 500 cm² (a=250 cm). The spacing between the pair is 136 cm. The inner pair is also a square with an area of 40 000 cm² (a=200 cm) and nests within the outer coil. The spacing between the pair is 110 cm. The innermost pair is again a perfect square of 50 625 cm² (a=225 cm) with 123 cm spacing between the pair and is nested within the other two coils. The wrapped coils were installed into the cage in a certain orientation based on several factors. First and foremost was the consideration of the ambient magnetic field at the proposed cage location. The geomagnetic field is commonly defined with +x pointing north, +y pointing east and +z pointing down. The cage axes were selected to match this definition (Brewer, 2012). The coils controlling the z axis are the largest coils. The next consideration involved the x or north component of the ambient magnetic field, which is larger than the y or east component. If the direction of the x component needed to be reversed, a higher magnitude magnetic field would be required than that required to flip the y direction magnetic field. Larger magnetic fields are generated by smaller coils which have the same current and number of coils, but it also has a smaller uniform volume, so a large field will give a higher deviation; thus the smallest coil was selected to control the x direction. Therefore, the remaining middle-sized coil controls the y direction (Brewer, 2012). The final cage is shown in Fig. 5.

Figure 5 Tri-axial square Helmholtz coil calibration facility at Alibag Magnetic Observatory.

Figure 6 The Bakelite bracket is used to roll the coil at the edges and ensures additional stiffness.

Figure 7 The coils are supported by a borosilicate glass piping construction to electrically isolate the coils from the support structure. The primary glass support structure is joined to the end corners using a female square-design six-way cross aluminium connector to which a Bakelite bracket is fixed using a nut and bolt.

3 Tri-axial square Helmholtz coil system: control and data acquisition

The system includes a CCS and a data logger. The CCS, which has been developed in-house, is an electronic unit which feeds an ultra-stable and accurate current into the coil, by which a known and stable magnetic field is generated. This magnetic field is then sensed by the magnetometer and logged into the data logger. The CCS is designed to provide a stable constant current of 1 mA to 1 A with steps of 20 µA. The coil constants and current resolution provide a magnetic field of at least ≈ 1.5 nT [20 µA × coil constant nT mA⁻¹]. It can supply a maximum of 1A current to the coil which can produce enough magnetic field to calibrate any magnetometer (fluxgate, proton precession magnetometer, Overhauser etc.) within the range of nT to mT. The CCS mainly consists of three components of which DAC LTC1657 is the key component, providing an ultra-stable current. LTC1657 is a parallel 16 bit rail-to-rail micropower DAC and provides an ultra-stable analogue voltage output for the given 16 bit digital inputs. The output of DAC is amplified by a gain of 3 with the op-amp; thus the minimum output voltage resolution achieved by the DAC is 187.5 µV. Current feeding to the coil from the CCS is referenced to a high-precision power resister of 10 Ω and hence the minimum current resolution achieved is 18.75 µA. Considering the noise performance of the DAC and the PCB board we have achieved up to 20 µA stable output current step to the coil. The CCS can feed a stable current in the range of 1 mA to 1 A to the coil system, which corresponds to (1 mA × 68.44 nT mA⁻¹) 68.44 nT minimum and (1 A × 68.44 nT mA⁻¹) 68 440 nT maximum magnetic field with the steps of ≈ 1.5 nT. LTC1657 is chosen because of its very low deglitched voltage output of 8 nV max and differential non-linearity (DNL) of ±1 LSB max (refer data sheet of LTC1657). The other useful feature of LTC1657 is the stable internal reference voltage and internally buffered output voltage that makes this IC very appropriate for our application. The second key component is the op-amp LT1014 and 2N3055 power transistor. These deliver a constant current to the coil system. The 2N3055 power transistor is NPN silicon which has a high power rating and a very low temperature drift. The op-amp and transistor configuration make a very accurate constant current source whose input is fed by the DAC. The third component is the digital inputs feeding to the DAC. It comprises of 5-digit rotatory BCD switches for human input to set the current value, CD4510 presetable up/down counters and CD4040 ripple binary counters. The CCS circuit operates on a stable ±12 V DC supply, although a few of the integrated circuits (ICs) work on +5 V DC which is provided by the main +12 V supply through a +5 V voltage regulator. It is very important to have a high-quality ground for this circuit to work efficiently. Here ground noise is kept below 1 mVpp. There are three electronic boards for each coil of the Helmholtz coil system and all three are identical in design. Provision is made to reverse the current in all the three coils by using a two-pole two-way toggle switch. This enables the CCS to generate a magnetic field in every possible direction in the coil, and thus calibration accuracy improves.

Figure 8 The sensor to be calibrated is mounted on a non-magnetic table referred to as the test stand, which is placed at the centre of the Helmholtz cage.

Figure 9 Fluxgate calibration using a h coil (sensor no. 1).

Figure 10 Fluxgate calibration using a d coil (sensor no. 1).

Figure 11 Fluxgate calibration using a z coil (sensor no. 1).

Figure 12 Fluxgate calibration using a h coil (sensor no. 2).

Figure 13 Fluxgate calibration using a d coil (sensor no. 2).

Figure 14 Fluxgate calibration using a z coil (sensor no. 2).

4 Calibration of the fluxgate magnetometers using the open-loop tri-axial square Helmholtz coil system

Very precise Earth magnetic field measurements have been made in space using fluxgate magnetometers in combination with scalar magnetometers (Musmann and Afanassiev, 2010), but only a few detailed descriptions about the theory and how to design and calibrate space fluxgate magnetometers have been published. The goal of this experiment was to determine whether or not the fluxgate can be calibrated using this system. The tested fluxgate sensor, referred to as the EUT (equipment under test) (Fig. 8), is a tri-axial fluxgate magnetometer procured from Watson Industries Inc., 3035 Melby St., Eau Claire, WI 54703, USA (Watson Industries, 2015). The sensor is mounted on a non-magnetic table, referred to as the test stand, which is placed at the centre of the Helmholtz cage. The test stand is made out of non-magnetic material and can be adjusted to various heights using a spirit level of 6 s sensitivity. The sensor is mounted so that sensor axes are aligned along the h, d and z directions. When using a CCS the magnetic fields along the three directions can vary. A set of measurements is tabulated by passing currents ranging from 50 to 500 mA through one of the coils in the forward and reverse directions. The input field in nT is calculated using the following formula. Similarly, the other two components can be calibrated.

$${\displaystyle }\mathrm{\text{Input field}}=\text{initial field}+\left(\text{input current}\times \text{coil constant}\right)$$

The fluxgate provides all three axes of magnetic field data as analogue voltages in the range of ±10 V output, which corresponds to ±60 000 nT (since 1 V ⇒ 6000 nT). This output is fed to a data logger, referred to as the nTLOGGER. ADAM-4017, which is a part of the nTLOGGER, which is a 16 bit commercially available A-D converter, converts inputs from three fluxgate sensors to digital form. It gives a resolution of ±4 nT. The nTLOGGER is a dual-core Intel-Atom-processor-based small data acquisition computer equipped with a GPS timing module developed in-house. It runs on a Windows operating system, containing the LabVIEW-based nTLOG data acquisition programme. Since the output of ADAM-4017 is in RS-485 format it is converted to RS-232 format by using ADAM-4520.

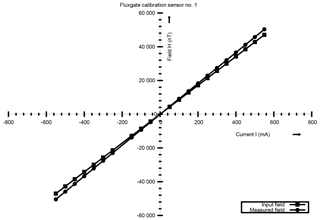
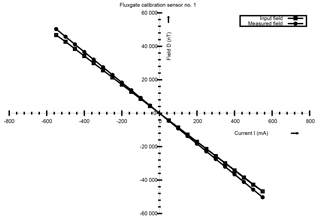
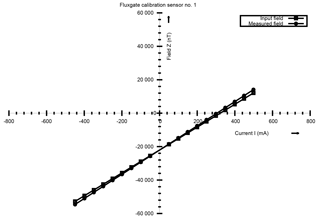
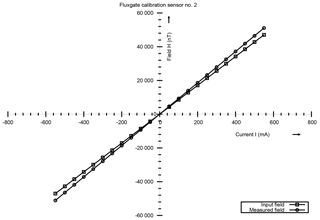
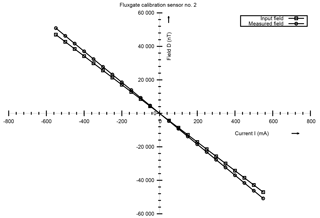
Figures 9, 10 and 11 show the comparison plots of input field and the measured field obtained for the three different coils and for one particular sensor. These results confirm that the field measured by the sensor is in agreement with the input current (input field) with a difference of a few nT at small currents and increasing to ≤ 1000 nT at higher inputs. This behaviour is attributed to the sensor alignment at the centre of the cage. For repeat experiments conducted on any random day and for three more sensors, the repeatability of the results is observed and hence we conclude that the system (mechanical hardware and the electronics) is stable against thermal changes. The curves for one more sensor is shown in Figs. 12, 13 and 14.

5 Conclusions

The measured fields in the cage volume are influenced by the natural variations due to the geomagnetic field. This system, being an open-loop system, has no feedback mechanism for the cancellation of these variations. To negate the effects of these geomagnetic fields a closed-loop system has to be implemented. We are in the process of designing such a mechanism. Further, the mechanical structure of a tri-axial system necessarily becomes rather complicated, and the systems described so far have a tendency to be heavy and bulky. This problem is believed to be overcome by a compact spherical coil system. We are also in the design stage of the circular Helmholtz coil system.