the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Daedalus: a low-flying spacecraft for in situ exploration of the lower thermosphere–ionosphere
Theodoros E. Sarris
Elsayed R. Talaat
Minna Palmroth
Iannis Dandouras
Errico Armandillo
Guram Kervalishvili
Stephan Buchert
Stylianos Tourgaidis
David M. Malaspina
Allison N. Jaynes
Nikolaos Paschalidis
John Sample
Jasper Halekas
Eelco Doornbos
Vaios Lappas
Therese Moretto Jørgensen
Claudia Stolle
Mark Clilverd
Ingmar Sandberg
Panagiotis Pirnaris
Anita Aikio
The Daedalus mission has been proposed to the European Space Agency (ESA) in response to the call for ideas for the Earth Observation program's 10th Earth Explorer. It was selected in 2018 as one of three candidates for a phase-0 feasibility study. The goal of the mission is to quantify the key electrodynamic processes that determine the structure and composition of the upper atmosphere, the gateway between the Earth's atmosphere and space. An innovative preliminary mission design allows Daedalus to access electrodynamics processes down to altitudes of 150 km and below. Daedalus will perform in situ measurements of plasma density and temperature, ion drift, neutral density and wind, ion and neutral composition, electric and magnetic fields, and precipitating particles. These measurements will unambiguously quantify the amount of energy deposited in the upper atmosphere during active and quiet geomagnetic times via Joule heating and energetic particle precipitation, estimates of which currently vary by orders of magnitude between models and observation methods. An innovation of the Daedalus preliminary mission concept is that it includes the release of subsatellites at low altitudes: combined with the main spacecraft, these subsatellites will provide multipoint measurements throughout the lower thermosphere–ionosphere (LTI) region, down to altitudes below 120 km, in the heart of the most under-explored region in the Earth's atmosphere. This paper describes Daedalus as originally proposed to the ESA.
- Article
(11327 KB) - Full-text XML
- BibTeX
- EndNote
1.1 Science context
The Earth's upper atmosphere, which includes the lower thermosphere and ionosphere (LTI), is a complex dynamical system, responsive to forcing from above and below: from above, solar radiation, solar wind and solar disturbances such as flares, solar energetic particles and coronal mass ejections cause strong forcing through many complex processes and produce ionization enhancements, electric fields, current systems, heating and ion-neutral chemical changes, which are not well-quantified. From below, the LTI system is affected by atmospheric gravity waves, planetary waves and tides that propagate through and dissipate in this region, with effects that are poorly understood. The response of the upper atmosphere to global warming and its role in the Earth's energy balance is also not well-known: whereas the increase in CO2 is expected to result in a global rise in surface temperatures, model simulations predict that the thermosphere may cool instead (Rishbeth and Roble, 1992), leading to thermal shrinking of the upper atmosphere. However, there is disagreement about the exact cooling trends (Qian et al., 2011; Laštovička, 2013). Quantifying the resulting secular variation in lower thermospheric density is needed for understanding the interplay of solar and atmospheric variability, and it will be critical in the near future, as increased levels of orbital debris cause increased hazards for space navigation, since lower density leads to a slower rate of removal of objects in low-Earth orbit (LEO) (Solomon et al., 2015). Measurements in the thermosphere are also essential for understanding the exosphere and modeling its altitude density profile and its response to space weather events (Zoennchen et al., 2017), as all exospheric models use parameters from this region as boundary conditions. During geomagnetic storms and substorms, currents with increased amplitudes close through the LTI, producing enhanced Joule heating (Palmroth et al., 2005; Aikio et al., 2012) and leading to significant enhancements in neutral density at high altitudes, which results in enhanced satellite drag. Geomagnetic storms also enhance the ionospheric scintillation of global navigation satellite system (GNSS) signals, which severely degrades positional accuracy and affects the performance of radio communications and navigation systems (Xiong et al., 2016). Sudden enhancements in the current system that closes within the LTI induce currents on the ground, termed geomagnetically induced currents (GICs); the impact of the largest GICs on power transformers in electrical power systems has, on occasion, been catastrophic and is now included in many national risk registers as it is considered a threat to technology-based societies should an extreme solar event occur (Pulkkinen et al., 2017); even repeated smaller events can stress transformers and reduce their operational lifetime (MacManus et al., 2017). Despite its significance, the LTI is the least measured and understood of all atmospheric regions; in particular, the altitude range from ∼100 to 200 km, where the magnetospheric current systems close and where Joule heating maximizes, is too high for balloon experiments and too low for existing LEO satellites due to significant atmospheric drag. Furthermore, few spectral features emanate from this region; these have been exploited by recent remote sensing spacecraft and from ground instrumentation, but despite these advances, this region remains under-sampled with many open questions. For example, no dataset is currently available from which the LTI energy budget can be confidently derived on a global basis. Thus, it is not surprising that scientists often informally refer to this region as the “ignorosphere”. The ever-increasing presence of mankind in space and the importance of the behavior of this region for multiple issues related to aerospace technology, such as orbital calculations, vehicle reentry and space debris lifetime, together with its importance in global energy balance processes and in the production of GICs and GNSS scintillation, make its study a pressing need.
1.2 Preliminary mission concept overview
The target of the proposed Daedalus mission is to explore the lower thermosphere–ionosphere by performing in situ measurements of ion, electron and neutral temperature and density, ion drift, neutral wind, ion and neutral compositions, electric and magnetic fields, and precipitating particles. Daedalus is composed of a primary instrumented satellite in a highly elliptical, dipping polar orbit, with a nominal perigee of < 150 km, a threshold apogee above 2000 km and goal apogee above 3000 km to ensure a sufficiently long mission lifetime (> 3 years), a high-inclination angle (> 85∘) and a number of deployable subsatellites in the form of CubeSats; four CubeSat subsatellites are baselined herein, but alternative mission concepts with larger subsatellites shall also be considered in the upcoming mission definition phases. The main satellite performs several short (e.g., days-long) excursions down to < 120 km (perigee descents) using propulsion, measuring key electrodynamic properties through the heart of the under-sampled region. At selected excursions, the main satellite releases the subsatellites using the standardized Poly-Picosatellite Orbital Deployer (PPOD) CubeSat release mechanism. The subsatellites perform a multiday to months-long orbit that gradually reduces their apogee altitude due to atmospheric drag, eventually burning up in the mesosphere. During each subsatellite release, measurements by the main satellite and the subsatellite on a string-of-pearls configuration at lowest perigee enable differentiation between the temporal and spatial variability of key electrodynamics processes; after the main satellite's ascent to nominal perigee altitude, co-temporal measurements by the main satellite at higher altitude and the subsatellite below offer unique and unprecedented synchronized two-point measurements through the LTI region. This measurement scheme allows for the investigation of cause and effect at different altitudes and offers the opportunity to measure, for the first time, the spatial extent and temporal evolution of key under-sampled phenomena in the LTI.
This paper describes the original Daedalus mission concept as proposed to the ESA in response to a call for ideas for the 10th Earth Explorer mission. The proposed concept has evolved from previous work carried out in the context of an ESA–GSTP (General Support Technology Program) study that was performed as part of the Greek Task Force in 2009 (Sarris et al., 2010), with a different set of constraints and accessible spacecraft and measurement technology. Upcoming phase-0 activities have been put in place to review and consolidate the concept, design and requirements within the new set of boundary conditions associated with the Earth Explorer program.
1.3 Measurement gaps in the LTI
The lowest in situ scientific measurements performed in this region by orbiting vehicles were made by the Atmosphere Explorer (AE) series of satellites in the 1970s. The perigee of these satellites extended as low as 140 km, but the dynamic range of some of the key measurements, such as mass spectrometer composition, made the data interpretation difficult at low altitudes. Since then, in situ measurements in the LTI have been limited to short crossings by sounding rockets, which by nature give only a snapshot of the LTI over a single location, whereas, for example, to understand the spatial structure and temporal evolution of key processes in response to a multi-hour solar storm, longer-term observations are required across different locations. Density measurements as low as 130 km have been inferred from the decay of low-altitude surveillance satellites and have been useful for understanding the gross features of the lower thermosphere, but the electrodynamics and composition of the transition region between 100 and 200 km remain obscure. At higher altitudes, a series of spacecraft have provided measurements of electric fields and density (CHAMP, DEMETER, GRACE, C/NOFS), but these are far from the transition region, which remains under-sampled. Thus, information on this region arrives almost exclusively from remote sensing, either from satellites (SME, UARS, CRISTA, SNOE, TIMED, ENVISAT, AIM) or from various ground experiments (lidars, ionosondes, incoherent scatter radars, coherent scatter radars, auroral imagers, photometers and Fabry–Pérot interferometers). There is a wealth of information that these measurements are providing, and there are significant advances in LTI science that have been accomplished, but there are also limitations that arise from the nature of remote sensing techniques. For example, neutral density, composition and temperature measurements are unfortunately not possible or are largely inaccurate in the 100–200 km region, as radiances become too weak and nonthermal above that altitude (Emmert, 2015; Prölss, 2011). Some major species composition information is obtained by a combination of ultraviolet (UV), infrared (IR) and Fabry–Pérot interferometer (FPI) measurements, but there is a significant gap in the obtainable profiles at ∼100–200 km due to a lack of appropriate emissions for observation. It is also noted that different observation methods may produce large deviations (even orders of magnitude) in estimates of key parameters in the LTI, such as conductivity, ion drifts and neutral winds, with no baseline dataset for comparison.
The main scientific objectives are twofold: on the one hand, Daedalus will quantify, for the first time, the key unknown heating processes in the LTI, in particular the largely unknown Joule heating as well as energetic particle precipitation heating, investigating how these affect the dynamics and thermal structure of the LTI and how the density, composition and temperature of the LTI vary during periods of enhanced heating associated with extreme space weather events. On the other hand, Daedalus will investigate the temperature and composition structure of the LTI in order to address a number of open questions, such as the following: the processes that control momentum and energy transport and distribution in one of the most unknown regions, the transition region at 100–200 km; the relative importance of the equatorial dynamo in driving the low-latitude ionosphere; the coupling of ions and neutrals in the low-altitude ionosphere and thermosphere; the role of the LTI region as a boundary condition to the exosphere above and stratosphere below; and the effects of the LTI region on the dynamics of the exosphere and stratosphere. These are discussed in further detail below.
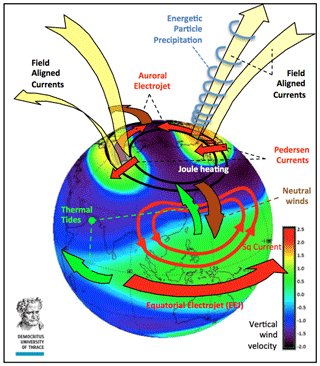
Figure 1Overview of the main processes affecting momentum and energy transport and distribution in the LTI.
2.1 Heating processes and energy balance in the LTI
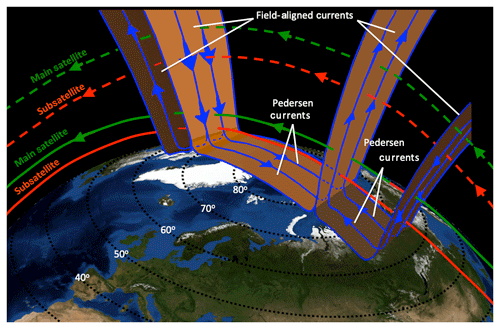
An overview of the energy and transport processes in the LTI resulting from the interaction with near-Earth space can be seen in Fig. 1, showing the complexity of simultaneous processes such as the following: incoming energy from solar and magnetospheric processes; the lower atmosphere driving the low-latitude ionosphere; Joule heating at higher latitudes; energetic particle precipitation (EPP) along field lines at high latitudes; the auroral electrojet – the large ( A) horizontal currents that flow in the E-region (90–150 km) in the auroral ionosphere; and the equatorial electrojet (EEJ) – the large eastward flow of electrical current in the ionosphere that occurs near noon within 5∘ of the magnetic Equator. Radiative heating of the LTI by extreme ultraviolet light (EUV) and x-rays from the Sun varies strongly with the 11-year solar cycle and is responsible for the large temperature increase above the mesopause at about 100 km of altitude. Its energy input is well-measured; however, after subtracting the solar cycle variations, a long-term cooling is predicted through atmospheric general circulation models (Rishbeth and Roble, 1992); this was found to be 10–15 K per decade through radar data over 33 years (Ogawa et al., 2014). This is attributed to anthropogenic greenhouse cooling because of the increasing absorption of infrared radiation. Joule heating, auroral particle precipitation and the solar deposition of energy maximize in the altitude range 100–200 km. At the same time, the composition between molecular and atomic species varies with the electrodynamic energy input and atmospheric forcing, as well as with particle precipitation. These composition variations in turn significantly modulate the efficiency of radiative heating in both EUV and infrared radiation. The 100–200 km region also involves large gradients and variability in various parameters such as winds, temperature, density and composition; these parameters show different behavior between different latitudes. The processes that control momentum and energy transport are strongly tied to the spatial and temporal variations of winds, temperature, density and composition; thus, whereas there is a fairly good physical understanding of energy transport processes, there are few measurements of how the energy is redistributed, hindering the exact quantification of these processes and their accurate modeling. Specifically, there is a lack of measurements of E-region electric fields, ion drifts and ion composition as well as simultaneous measurements of neutral winds and neutral composition.
Table 1Main energy deposition mechanisms and their ranges in the LTI region, as well as the available energy within the solar wind during moderate conditions.
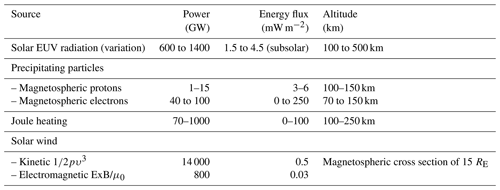
Estimates of the range of energy deposition mechanisms in the LTI by each of the main heating processes discussed above are presented in Table 1. The global power values over both hemispheres are adapted from Knipp et al. (2005), who used models for these estimates; minimum values correspond to the average power during solar minimum, whereas maximum values correspond to the top 1 % of heating events. Approximate values for the global power for Joule heating, obtained from data analysis and modeling, are based on Palmroth et al. (2005) and Fedrizzi et al. (2012). The solar wind fluxes listed are only indicative and correspond to average conditions (proton density of ∼5 cm−3 and solar wind speed of ∼400 km s−1). The corresponding fluxes over a cross section corresponding to ∼15 RE of the magnetosphere's radius translate to 14 000 and 800 GW for the solar wind kinetic energy and electromagnetic flux, respectively; see, e.g., Koskinen and Tanskanen (2002). For active conditions a higher power is available in the solar wind, for example 18 000 GW for a solar wind speed of 800 km s−1 and a radius of 7.5 RE; see, e.g., Buchert et al. (2019). Only a highly variable fraction of this solar wind power is extracted by magnetospheric processes and dissipated in the Earth's LTI. However, this fraction can at active times exceed the normally dominant heating by the absorption of EUV. The energy flux values listed in Table 1 are locally measured in LEO for solar EUV (Lean, 2009) and with incoherent scatter radars (ISRs) for electron precipitation and Joule heating; see, e.g., Semeter and Kamalabadi (2005), Virtanen et al. (2018), Aikio and Selkälä (2009), Aikio et al. (2012), Cai et al. (2013). In particular, Virtanen et al. (2018) have shown that in narrow auroral arcs electron precipitation may be associated with energy input as high as 250 mW m−2. For Joule heating, Aikio and Selkälä (2009) and Aikio et al. (2012) have shown that energy fluxes reaching up to 100 mW m−2 are often seen; see, e.g., Figs. 14–17 of Aikio and Selkälä (2009). What is evident from this table is that the energy deposition processes with the largest significance and variation locally, which can range from comparatively insignificant energy flux levels to the single largest source, are Joule heating and energetic particle precipitation. Particularly at high latitudes and at times of large solar and geomagnetic activity, the Earth's magnetic field couples the LTI to processes in the magnetosphere and the solar wind, which provide heating that rivals or even exceeds the heating of the radiative component. The quantification and parameterization of these processes make up one of the primary science objectives of Daedalus.
2.1.1 Joule heating
Joule heating is caused by collisions between ions and neutrals in the presence of a relative drift between the two (Vasyliūnas and Song, 2005). Ion-neutral friction tends to drive the neutral gas in a similar convection pattern to that of the ions, which with time also generates kinetic energy (Codrescu, 1995; Richmond, 1995). Such drifts are driven by processes in the magnetosphere and involve current systems between space and the ionosphere. These currents, marked in Fig. 1 as field-aligned currents, were first envisaged by Birkeland more than 100 years ago (Birkeland, 1905): they flow parallel to the magnetic field, and they electrically couple the high-latitude ionosphere with near-Earth space. The strength of these currents and their structure depend on solar and geomagnetic activity. In space they are well-characterized by a number of missions with multipoint measurement capabilities, such as the ESA's four-spacecraft Cluster mission (Amm, 2002; Dunlop et al., 2002) and the AMPERE mission, using magnetometer measurements from the Iridium satellites (Anderson et al., 2000). However, the closure of these current systems, which occurs within the LTI with a maximum current density within the 100–200 km region, is not well-sampled. This leads to large uncertainties in understanding and quantifying Joule heating in this region. Joule heating is the most thermodynamically important process dissipating energy from the magnetosphere, and it affects many thermospheric parameters, such as wind, temperature, composition and density, in a very significant way; it is thought that its effects on the upper atmosphere are more significant than energetic and auroral particle precipitation (e.g., Zhang et al., 2005), even though the exact ratio has not been successfully quantified to date. In a major magnetic storm, Rosenqvist et al. (2006) estimated the power input into the magnetosphere to be ∼17 GW by extrapolating data from the Cluster mission; about 30 % of this power could be dissipated as Joule heating in the ionosphere–thermosphere, as inferred from EISCAT radar measurements and AMIE modeling. However, as discussed below, there are great discrepancies in estimating Joule heating, depending on the methodology and measurements used.
One of the big unknown parameters involved in Joule heating, and one of the issues that could be a source of the largest discrepancies in its estimates, involves neutral winds, as Joule heating depends on the difference between ion and neutral velocities in a complex way (Thayer and Semeter, 2004). For example, in the auroral oval the role of winds during active conditions is to increase Joule heating in the morning sector but to decrease it in the evening sector (Aikio et al., 2012; Cai et al., 2013). Due to a lack of colocated and co-temporal measurements, neutral winds are usually neglected, and currently height-integrated Joule heating is more commonly estimated in one of the following ways: (i) from the product of the electric field and the height-integrated current density, E⋅J; (ii) from the product of the height-integrated Pedersen conductivity, ΣP, and the square of the electric field, ΣPE2, where ΣP is estimated from models; or (iii) from the Poynting theorem, estimating the field-aligned Poynting flux, in which the magnetic field is obtained through differences between measured and modeled values. An overview of various methods to estimate height-integrated Joule heating is described in Olsson et al. (2004).
Rocket flights are one of the key methods of accurately sampling Joule heating in situ; the methodology and required measurements for obtaining in situ Joule heating estimates are described in Sect. 3.3. Such measurements have shown that Joule heating maximizes in the range from 110 to 160 km, which is also the altitude range where Pedersen conductivity maximizes; for example, the Joule-2 rocket campaign has shown that the altitudes of maximum Joule heating were at 118 km (e.g., Sangalli et al., 2009), even though results from different rocket flights vary considerably (Robert Pfaff, personal communication, 2019). A key limitation of rocket flights is that they can only provide snapshots of Joule heating estimates over the rocket launch site, without information on the latitudinal distribution or temporal evolution.
Together with rocket flights, datasets that have traditionally been used for Joule heating estimates include measurements from ground radars (Ahn et al., 1983; Aikio et al., 2012) and from low-altitude satellites, such as AE-C (Foster et al., 1983), DE-1 and DE-2 (Gary et al., 1994) and Astrid-2/EMMA (Olson et al., 2004). Of these measurements DE-1 and DE-2 were the only spacecraft that performed simultaneous neutral wind and electric field measurements; however, they only went down to 567.6 and 309 km, respectively, and even though the region that the DE spacecraft sampled is certainly heated up after the deposition of energy in the E-region, it is well above the region where Joule heating maximizes. Estimates of Joule heating have also been based on empirical models such as the Assimilative Mapping of Ionospheric Electrodynamics (AMIE) procedure (Chun et al., 1999; Slinker et al., 1999), the Grand Unified Magnetosphere–Ionosphere Coupling Simulation (GUMICS-4) magnetohydrodynamic (MHD) model (Palmroth et al., 2004, 2005), the Lyon–Fedder–Mobarry (LFM) MHD model (Lopez et al., 2004; Hernandez et al., 2005; Slinker et al., 1999), the Compiled Empirical Joule Heating (CEJH) empirical model (Zhang et al., 2005), the Open Global General Circulation Model (OpenGGCM) coupled with the Coupled Thermosphere–Ionosphere Model (CTIM) and the Coupled Thermosphere–Ionosphere–Plasmasphere electrodynamics (CTIPe) model (e.g., Connor et al., 2016). Through such modeling and model–data comparisons the driving of Joule heating is believed to be well-understood: for example, MHD modeling has shown that Joule heating is controlled directly by the solar wind dynamic pressure (e.g., Lopez et al., 2004; Hernandez et al., 2005). However, the quantification of Joule heating is still an unresolved issue, with great discrepancies between different modeling approaches.
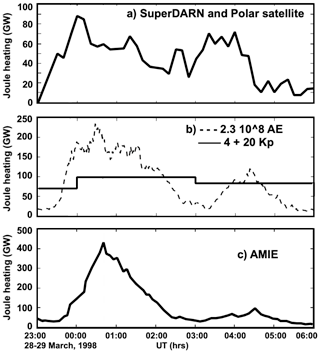
Figure 2Discrepancies between global integrated Joule heating as estimated by (a) SuperDARN and Polar measurements, (b) AE- and Kp-based proxies, and (c) the AMIE procedure during a solar storm (adapted from Palmroth et al., 2005).
The uncertainty in obtaining accurate Joule heating estimates between the various methods is evident in Fig. 2, by Palmroth et al. (2005), in which Joule heating is calculated three different ways that are commonly used: panel (a) shows measurements from the Super Dual Auroral Radar Network (SuperDARN) used combined with Polar satellite measurements; in panel (b) it is estimated through parameterizations that are used commonly, using empirical relationships with the AE and Kp indexes as proxies; and in panel (c) it is estimated by using the AMIE assimilation model from the National Center for Atmospheric Research (NCAR). What is particularly striking in this plot is that there is up to a 500 % difference among some of these estimates. Furthermore, it can be seen that there is a significant difference on the timing (timescale is in hours) of when Joule heating starts: there is almost an hour difference in the onset and peak of Joule heating. This is due to the lack of in situ measurements wherein Joule heating occurs and is an issue that is wide open to date. It is therefore of critical importance to fully understand the basic properties of Joule heating and to fully quantify and parameterize its effects in order to understand the processes in the high-latitude ionosphere and thermosphere. The correct quantification of Joule heating is also essential in order to properly and accurately include it in models, thus being able to predict its relation to LTI dynamics and its contribution to the total energy balance. Some questions related to Joule heating that remain open are the following. (1) What is the dependence of Joule heating on geomagnetic activity and on energetic particle precipitation? (2) What is the relation of Joule heating to neutral wind, composition, temperature and density? (3) What is the Joule heating distribution in space and time? (4) What is the time constant for momentum transfer during Joule heating processes, and what is the dependence of this time constant on magnetospheric conditions and the thermosphere state? (5) What is the relation between Joule heating, upwelling and changes in neutral composition? (6) How is Joule heating affecting and/or driving neutral winds at low latitude, what is its impact in redistributing heat, momentum and composition, and how do these changes affect the lower atmosphere? (7) How much Joule heating is involved in the equatorial and midlatitude tidal dynamos in gravity waves, and how does it affect the neutral atmosphere dynamics?
Since it is the coupling of ions and neutrals that determines Joule heating, for an in-depth understanding of the Joule heating process and to perform Joule heating modeling accurately, simultaneous measurements of ion drifts, neutral winds, plasma and composition down to the E-region are crucial, together with measurements of the electric and magnetic fields, as described in further detail in Sect. 3.3. These measurements have never been performed in situ below 300 km, in the source region where Joule heating maximizes. There are radars that have made such colocated measurements remotely, but these were localized and provided a weakly constrained estimate of what is happening at 300 km. Daedalus employs a complete suite of measurements that will measure all the needed parameters to calculate Joule heating and the thermosphere response and also differentiate under which conditions different approximations for Joule heating could be valid. In order to quantify and understand the Joule heating process, local measurements at its source in the E-region where Joule heating maximizes are required. It is for this reason that the causal relationship of Joule heating to the thermosphere dynamics remains unresolved and that estimates vary so greatly.
2.1.2 Energetic particle precipitation
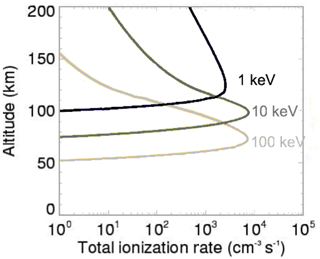
Energetic particle precipitation (EPP) is the second-strongest energy source after Joule heating, both in terms of magnitude and variation. Precipitating electrons, protons and energetic neutral atoms (ENAs) deposit their energy into the atmosphere at different altitudes, depending on particle energy. There are multiple effects caused by EPP: through the collisions with neutral particles at high latitudes, precipitating particles ionize the neutral gas of the lower thermosphere and dissociate atmospheric particles (Sinnhuber et al., 2012); they also heat up the lower thermosphere, produce bremsstrahlung x-rays and auroras, and increase the conductivity of the ionosphere. An estimate of the total ionization rate for EPP energies of 1, 10 and 100 keV is given in Fig. 3. In particular, the increased ionization leads to increased conductivity that facilitates the flow of current along the magnetic field lines and through the ionosphere, thus enhancing Joule heating. However, the direct relationship between EPP and conductivity has not been established. It is therefore important to measure EPP, conductivity and Joule heating at the same time. In addition, EPP (including energies much greater than 100 keV) significantly affects atmospheric composition directly via the production of HOx and NOx and indirectly through the descent of NOx to lower altitudes (Codrescu et al., 1997; Randal et al., 2007). HOx and NOx act as catalysts for ozone destruction in the mesosphere (e.g., Seppälä et al., 2004), which, through a complicated radiative balance involving the amount of UV, can lead to an impact on terrestrial temperatures within the polar vortex (Seppälä et al., 2009). EPP and solar particle forcing on the mesospheric chemistry can be so large that it can affect the atmosphere and climate system (Andersson et al., 2014), and therefore it has received growing attention from the Intergovernmental Panel for Climate Change (IPCC). The largest issue in relating the mesospheric ozone destruction with magnetospheric processes is that accurate estimations of the particle energy spectrum are lacking.
More energetic ions (E > 30 MeV) and electrons (E > 300 keV) penetrate down to the stratosphere, whereas the “medium-energy” ions (1 < E < 30 MeV) and electrons (30 < E < 300 keV) deposit their energy through ionization to the mesosphere and the lower-energy ions (E < 1 MeV) and electrons (E < 30 keV) to the thermosphere. ENAs, covering the energy range of ∼1 keV to ∼1 MeV, are produced via charge exchange when energetic ions interact with background neutral atoms such as Earth's geocorona. Most of the energy density of ENAs is in the ∼100 keV range. The energy transfer to the thermosphere due to precipitating ENAs can be significant, particularly during heightened geomagnetic activity. Since they do not follow magnetic field lines these particles play a role in mass and energy transfer to lower latitudes beyond the auroral zone (Fok et al, 2003). Measurements of EPP have been performed by multiple rockets as well as by various satellites; however, rocket measurements are by nature short in duration, essentially providing only snapshots of vertical profiles, thus failing to capture all phases of EPP and its effects on the LTI. EPP can also be estimated by inverting the electron density height profiles measured by ISRs (e.g., Semeter and Kamalabadi, 2005). Inversion methods are based on ionization rate profiles like those shown in Fig. 3, but the profiles depend on thermospheric density and temperature (Fang et al., 2010), which are taken from models. On the other hand, spacecraft such as POES, DMSP, SAMPEX, Polar and DEMETER have only performed EPP measurements at higher altitudes, failing to measure in situ the direct effects of EPP on lower thermospheric density, temperature and composition. Several of these missions were also limited by having particle detectors with wide energy channels (POES), whereas others could not resolve pitch angle distribution (DMSP). There is also considerable noise between the electron and ion channels onboard the POES SEM-2 instruments, making unambiguous measurements of EPP difficult (Rodger et al., 2010).
In summary, it can be stated that Joule heating and EPP are critical parameters in understanding high-latitude and midlatitude processes in the LTI. Many aspects of the Joule heating process are not well-characterized, and estimates of the energy deposition vary greatly depending on the calculation method. EPP is a critical parameter of high-latitude energy deposition that also affects Joule heating by altering conductivity. Combined measurements of neutral constituents and energetic particles (ions, electrons and neutral atoms) are critical in estimating EPP energy deposition and for a better understanding of ionosphere–thermosphere coupling; they will also allow scientists to resolve open questions about ion-neutral interactions. Understanding both processes is imperative for understanding the atmosphere as a whole.
2.2 Investigation of variations in the temperature and composition structure of the LTI
The second science objective of Daedalus involves the investigation of the temporal and spatial variability of key variables in the LTI system. An overview of this variability can be seen in Fig. 4, showing the extreme values of neutral temperature at different solar conditions (a), constituents of the thermosphere (b) and constituents of the ionosphere (c) as a function of altitude. These are further discussed in the following paragraphs.
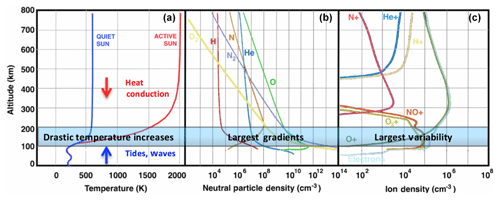
Figure 4Simulated key variables in the LTI as a function of altitude: temperature at quiet and active solar conditions (a), neutral (b) and ion (c) constituents. The altitude range from 100 to 200 km shows the largest rates of change in most variables.
2.2.1 Temperature structure of the LTI
In Fig. 4a, it can be seen that the region from ∼100 to 200 km is the transition region where the temperature increases drastically from the mesopause to the thermosphere; higher up (particularly above 300 km) the thermosphere is essentially isothermal. Temperature in the mesosphere (50 to 85 km) decreases with altitude, reaching a minimum at the mesopause; above that, in the thermosphere, temperature increases and may range from 500 to 2000 K depending on solar and other energy inputs, as well as on energy transport processes. The timescales of temperature variations within this region also vary significantly from the lower end to the upper end of the transition region: whereas in the mesosphere temperature measurements from ground-based lidars show a diurnal variation, remote sensing measurements of the region above 150 km show a semidiurnal variation. Many details of these timescales are not well-understood.
2.2.2 Composition structure of the LTI
A major characteristic of the neutral composition in the thermosphere is that, contrary to the mesosphere and stratosphere below, its main chemical constituents, N2, O2, O, He and H, tend to diffusively separate according to their individual scale heights. In particular, the region from ∼100 to 200 km, i.e., the region just above the turbopause, is believed to be the key area where this transition takes place: below a height of ∼105 km, turbulence mixes the various species of gas that make up the atmosphere, and the relative abundances of species tend to be independent of altitude. This turbulent mixing process is probably related to gravity wave breaking, but it is not known where and how the transition from turbulent mixing to molecular diffusion occurs or how it varies globally, annually or on other timescales. On the other hand, in the thermosphere above ∼200 km, composition is controlled by molecular diffusion; thus, heavier species are concentrated lower down, while the light ones dominate at higher altitudes so that, to first order, the density of each species decreases with altitude at a rate that is related to its mass, according to , where , mx is the mass of the species in atomic units and R is the gas constant. Due to this diffusive separation, the main species N2, O2 and O show variations in their densities that follow the lines in Fig. 4, as marked. From this figure, it can be seen that the LTI is where the composition balance changes from molecular species (N2, O2) to atomic species (O) and that O becomes the dominant species from ∼170 to 200 km up to the top of the thermosphere. Below 200 km N2 is the most significant species, whereas below about 120 km O2 is more significant than O (Wayne, 2000). The ratio between O and N2 is of particular importance, as it impacts the recomposition rate of O+, and thus it impacts the plasma density (Kelley, 2009). The O∕N2 ratio in turn is controlled by the state of atmospheric mixing (which is parameterized as the eddy diffusion in models) and by impacts of gravity waves, which are not well-understood (Jones et al., 2014, and references therein). O also plays an important role in the energy balance in the lower thermosphere: O is directly or indirectly responsible for almost all of the radiative cooling of the lower thermosphere by influencing the main radiative cooling terms, CO2 at 15 µm and NO at 5.3 µm (Gordiets et al., 1982), and it thus affects the response of the LTI to climate change. In particular, regarding NO, despite the great amount of community effort in measurements and modeling, the temporal and spatial variability and the magnitude of the concentration of NO observed in the lower thermosphere remain largely unknown. Quantifying the variability of O and O2 and the sources of this variability is thus a central challenge in upper atmosphere physics and will assist in obtaining a better theoretical understanding of upper atmosphere energetics and dynamics.
2.2.3 Science questions related to the temperature and composition structure of the LTI
In summary, temperature and composition structure in the lower thermosphere is extremely important for many processes and remains under-sampled to a large degree; many details of the timescales of its variation in the LTI region are not well-understood. Related to the second science objective, key science questions that will be addressed by Daedalus are the following. (1) What are the spatial and temporal variations in density, composition and temperature of the neutral atmosphere and ionosphere at altitudes of 100–200 km with respect to solar activity? (2) What is the relative importance of the equatorial and midlatitude tidal dynamos in driving the low- and middle-latitude ionosphere, and how do ions and neutrals couple? (3) What is the LTI region's role as a boundary condition in the exosphere above and stratosphere below, and how does it affect their energetics and dynamics?
3.1 Orbital requirements
To resolve the above open questions, there is a need for measurements at different altitudes throughout the LTI and down to extremely low altitudes, where key electrodynamics processes such as Joule heating and EPP maximize, for an extended time period. This is best realized by a spacecraft in a highly elliptical orbit, with a perigee that reaches as low as possible in the 100–200 km region; orbital simulations indicate that a nominal perigee of 150 km is feasible for a prolonged mission. In order to perform measurements below the “observation barrier” of 150 km, the spacecraft performs several perigee descents to lower altitudes, down to 120 km by use of propulsion. In order to perform measurements for a duration beyond 1 year, an apogee higher than 2000 km is required, as discussed below. Most dynamic processes in the LTI, in particular Joule heating, maximize at high latitudes; thus, a high-inclination orbit is preferred. Finally, in order to investigate the cause and effect of dynamic upper atmosphere processes and to unambiguously differentiate between spatial and temporal effects, co-temporal measurements at different altitudes are required. This can be achieved by releasing from the main satellite expendable subsatellites that carry minimal instrumentation and perform a spiralling orbit until they burn up in the mesosphere. Such multipoint measurements offer the opportunity to measure, for the first time, the spatial extent and temporal evolution of key under-sampled phenomena in the LTI.
3.1.1 Mission duration
The LTI is highly variable, being influenced by variations in the solar, auroral, tidal and gravity wave forcing. These variations occur over different timescales: the solar cycle (11-year), interannual (e.g., quasi-biennial), seasonal and, most importantly, diurnal. While multiyear missions to investigate solar cycle effects may be impractical in the LTI due to high atmospheric drag, it is important to perform measurements in the thermosphere and ionosphere for as much of the diurnal cycle as possible, sampling the same latitude more than once during each season. A high-inclination elliptical orbit, such as is required to address key science objectives in the LTI, means that the orbit precesses in latitude over time. In order to provide coverage of all latitudes and also to sample the LTI region at different seasons, the minimum mission duration is 1 year; 3 years would be ideal, as a 3-year mission will significantly enhance measurement statistics of the response of the LTI to solar events at different latitudes and will enhance the observational statistics of seasonal variations in key parameters and processes.
The mission lifetime will depend on a number of parameters, such as apogee selection, spacecraft mass and cross section, spacecraft drag coefficient, and the expected solar activity, which affects atmospheric density and the associated spacecraft drag. In Fig. 5 we plot the expected Daedalus lifetime in days for different launch dates; the different curves correspond to different spacecraft wet mass at launch (i.e., including propellant mass) and initial spacecraft apogee selection.
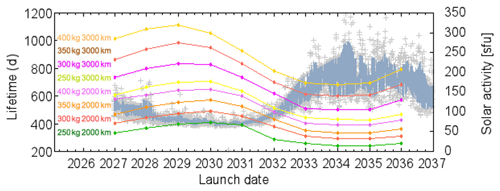
Figure 5Simulated Daedalus lifetimes as a function of launch date for a perigee of 150 km and for various values of apogee and spacecraft mass, as marked. It is noted that higher mass and apogee lead to longer lifetimes, whereas higher levels of solar activity lead to shorter lifetimes. Solar activity is plotted in terms of daily (gray crosses) and average (gray lines) values of the F10.7 index.
In the background of Fig. 5, the expected solar activity index F10.7 is calculated by Monte Carlo sampling of the past six solar cycles. Lifetime simulations were performed using ESA's DRAMA software, assuming a drag coefficient of 2.2 (suitable for a cylindrical satellite) and a total satellite drag area of 0.6 m2 (including the electric and magnetic field booms). It is noted that increasing apogee altitude increases the mission lifetime but leads to enhanced radiation exposure in the inner radiation belt. This should be studied as part of a trade-off analysis to be conducted during the initial Daedalus mission phases. Finally, it is emphasized that the simulated lifetimes in Fig. 5 correspond to natural decay times, which can be significantly enhanced with perigee and apogee maintenance by use of propulsion.
3.1.2 Measurement requirements
In order to obtain accurate estimates of the in situ Joule heating rate, which is part of the Daedalus primary mission objectives, a number of parameters need to be measured. These are described below through two different estimation methods for Joule heating. Details on the analysis presented here can be found in Richmond and Thayer (2000) and references therein.
By applying Poynting's theorem to the high-latitude ionosphere,
where W is the energy density in the electromagnetic field and S is the Poynting vector. Assuming quasi-steady state, the time rate of change of the electromagnetic energy density is negligible in the ionosphere, and thus it can be assumed that
The term j⋅E is the rate of the electromagnetic energy exchange. The ionospheric Joule heating rate is calculated in the reference frame of the neutral atmosphere; when the neutrals move with a velocity un, the electric field in the frame of the neutral gas E∗ is given as
where B is the magnetic field. Thus, the electromagnetic energy exchange rate in the ionosphere becomes
The first term on the right side is the Joule heating rate (W m−3) and the second term is the mechanical energy transfer to the neutral gas. Thus, the Joule heating rate becomes
j can, in principle, be inferred from magnetometer data, which is, however, not straightforward at altitudes where Pedersen, Hall and Birkeland currents coexist and contribute to the local magnetic field, i.e., roughly below 300 km. Alternatively, assuming quasi-neutrality, i.e., that the electron density Ne is equal to the sum of the ion species densities, the electric current density can be expressed as
where e is the elementary charge, and Vi and Ve are the ion and electron drifts, respectively. Inserting Eq. (6) into Eq. (5), we obtain
where and are the ion and electron drifts in the neutral gas reference frame. We divide un, E, Vi and Ve into components perpendicular and parallel to B.
At all ionospheric altitudes above the D-region (i.e., > 90 km) the electrons are magnetized because , where ve,n is the electron-neutral collision frequency and is the electron gyrofrequency; thus,
The parallel electron mobility is large enough to produce a very large parallel conductivity (); thus, the electrons move easily along the magnetic field, and they tend to sort out any field-aligned (i.e., parallel to magnetic field) electric fields. Thus, the electric field tends to be perpendicular to the magnetic field, and . Thus,
Using the identity , Eq. (9) reduces to
meaning that the Joule heating rate can be estimated by the ion current times the electric field. Taking into account that the ion population consists of many species, for an ion composition Nk, , Eq. (10) becomes
where, assuming charge neutrality,
As an approximation, it can be assumed that all ion species drift with the same velocity Vi, and thus Eq. (10) can be used. In situ measurements of ion drifts, neutral winds, Ne, and E and B in an arbitrary nonrelativistic reference frame (for example, the satellite's reference frame) allow for the estimate of the total local heating rate.
A different method to estimate Joule heating with in situ measurements involves Ohm's law applied to ionospheric plasma. From the ionospheric Ohm's law,
where b is the unit vector along the ambient magnetic field, and σP and σH are the Pedersen and Hall conductivities, respectively. The Hall current is non-dissipative, and the power transfer is achieved by the Pedersen current; thus, the ohmic heating rate is estimated as
In Eq. (14), the Pedersen conductivity, σP, can be calculated as
In Eq. (15), κk represents the ratio of each k species gyrofrequency versus its collision rate. The collision frequencies depend on a number of terms, such as the density and composition of the ion and neutral species, which need to be measured independently through mass spectrometry, the ion and electron temperatures, and the values for collision cross sections. The latter are calculated primarily through laboratory experiments with ion-neutral collisions. However, these may have systematic uncertainties in the upper atmosphere, and their accuracy has never been evaluated in situ. Daedalus will be able to provide estimates for the ion-neutral collision frequencies and the ion-neutral collision cross sections. The methodology is described below.
The ion momentum equation is given as
Assuming a homogenous plasma, and neglecting the gravity (g) and the thermal pressure (P) gradient terms whose contribution is negligible, in the reference frame of neutral winds (un=0), Eq. (16) becomes
and in the satellite frame,
If we also assume a steady state perpendicular to ,
Thus, from measurements of , and E⊥, we can estimate the ion-neutral collision frequency as
and with (Banks and Kockarts, Aeronomy, 1973) the ion-neutral cross section can be estimated as
where σi,n is the ion-neutral cross section, kB is the Boltzmann constant, Ti is the ion temperature and mi is the ion mass.
Daedalus will have a complete suite of instruments to compare the two methodologies presented above and to resolve which approximations are valid. Daedalus will also be able to test the validity of using laboratory estimates of ion-neutral collision cross sections in the upper atmosphere. To achieve the above, all the parameters that go into Joule heating calculation in a local volume of space need to be measured; in summary, the required measurements are neutral winds, ion drifts (along-track and cross-track), ion density, ion composition and ion temperature, electron temperature, neutral density, neutral composition (primarily N2, O, O2, N, NO), and neutral temperature, magnetic field and DC electric fields.
Table 2List of Daedalus instruments, measurements, estimated dynamic ranges, accuracies and sensitivities.
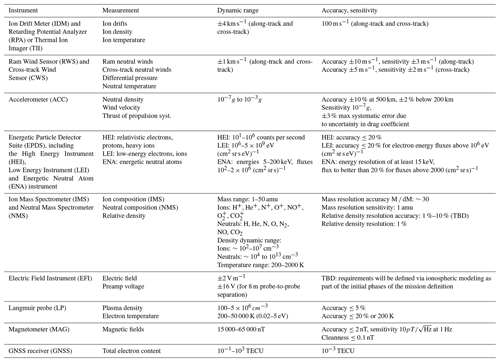
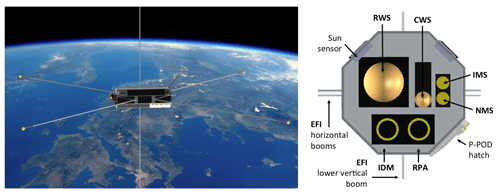
The proposed suite of instruments to perform measurements of the parameters that go into Joule heating and particle precipitation is listed in Table 2. The corresponding measured parameters, their dynamic ranges in the region of interest, and the required threshold accuracy and sensitivity for each observable are also listed. Key scientific instrumentation that is placed in the ram direction includes the Ion Drift Meter (IDM) and Retarding Potential Analyzer (RPA) or Thermal Ion Imager (TII), Ram Wind Sensor (RWS), Cross-track Wind Sensor (CWS), Ion Mass Spectrometer (IMS), and Neutral Mass Spectrometer (NMS). The total surface area of the ram direction instrumentation will determine the total cross section of the spacecraft, which affects the mission lifetime; hence, care should be taken during the initial mission phases to minimize the total ram instrument surface. Three-axis stabilization is required for the instruments (IDM and RPA or TII, RWS–CWS, IMS–NMS), with stringent attitude control and pointing knowledge requirements. The complete list of instruments, including their requirements in order to address the scientific objectives of Daedalus, is presented in Sect. 4.2.
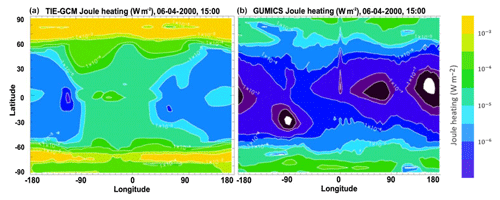
Figure 6Joule heating from TIE-GCM (a) and GUMICS (b) for the storm of 6 April 2000 (from Sarris et al., 2013). The TIE-GCM results cover latitudes from −87.5 to 87.5∘. The GUMICS modeling domain covers the high latitudes, at which the code is coupled to the magnetosphere, while at the low and middle latitudes the results represent a continuity over a sphere.
One of the uses of the in situ estimates of Joule heating from the above measurements will be to provide anchor points that can constrain existing models of Joule heating, estimates of which vary considerably: as an example, in Fig. 6 simulation results for Joule heating are plotted based on two physics-based models, the Thermosphere–Ionosphere–Electrodynamics General Circulation Model (TIE-GCM) in panel (a) vs. the Grand Unified Magnetosphere–Ionosphere Coupling Simulation (GUMICS) in panel (b), for the same instance during the storm of 6 April 2000 and with the same dynamic range for Joule heating (same color scale). The GUMICS-4 modeling domain covers only the high latitudes, where the code is coupled to the magnetosphere, while the results at low and middle latitudes merely represent a continuity over a spherical ionospheric domain. This means that the results can be compared at high latitudes only. A large discrepancy is seen between the two models, both in total amplitude and in the spatial features. A spacecraft that performs measurements of the actual parameters that go into Joule heating at various altitudes, in particular in the region where it maximizes, is the only way to provide an accurate reference for models and to identify missing physics or inaccurately derived parameters.
As a preliminary step towards identifying the observation requirements of Daedalus, a number of upper atmosphere models have been run and intercompared in order to simulate the measurement performance requirements and dynamic ranges of the proposed instruments. These models, together with the corresponding outputs that are related to Daedalus, are listed below.
-
TIE-GCM: Tn, Ti, Te, zonal, meridional and vertical neutral winds, O, O2, O+, , NO+ (Richmond et al., 1992; Richmond and Maute, 2014)
-
GUMICS-4: magnetic field, electric field, Pedersen and Hall conductivities, energetic particle precipitation energy deposition, Joule heating, field-aligned currents (Janhunen et al., 2012)
-
IRI-07: Ne, Te, Ti, O+, , NO+ (Bilitza and Reinisch, 2008, and references therein)
-
NRLMSISE-00: Tn, O, O2, neutral density, collision frequency (Picone et al., 2002, and references therein)
-
FMI – alpha parameter: Pedersen to Hall conductivity ratio (Juusola et al., 2007)
-
HWM-07: zonal and meridional neutral winds (Drob et al., 2008)
-
Weimer (2005): ionospheric electrostatic potential (Weimer, 2005a, b)
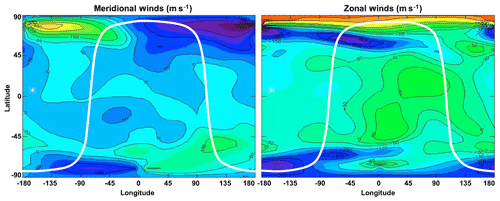
As an example of the sampling of some of the above variables by Daedalus, the simulated storm-time zonal and meridional winds are shown in Fig. 7; the simulated ground track of the orbit of a spacecraft that is sampling these winds is also plotted.
The dynamic ranges of these variables (i.e., the geophysical quantities to be observed by Daedalus) were estimated by running the above models through extreme (minimum and maximum) geomagnetic activity conditions; in addition, the sensitivity of the variables to model input parameters was investigated. An error analysis was conducted that modeled the sensitivity of the resulting Joule heating to errors in obtaining each of these variables. A summary of the preliminary estimates for the dynamic range in the region of interest, as well as the threshold accuracy and sensitivity of the proposed key instrumentation, is listed in Table 2; these will need to be redefined through a trade-off analysis as part of the initial phases of the mission development through an iterative process that involves science goals, instrument specifications, spacecraft capabilities and mission (orbit) analysis.
4.1 Orbital design
Addressing the scientific objectives of Daedalus requires a spacecraft in a high-inclination (> 8∘) orbit that can perform measurements at high latitudes within the altitude range of 100–200 km for a threshold duration of 1 year and a goal duration of more than 3 years in order to capture the response of the LTI region during all seasons and at all latitudes. Preliminary orbital simulations indicate that this is feasible by a spacecraft with a perigee as low as 150 km and apogee higher than 2000 km. By using an efficient propulsion system, the total mission duration can be significantly increased (up to several years). The need to minimize atmospheric drag is best realized by a torpedo-shaped spacecraft with a minimal cross section towards the ram direction and with body-mounted solar panels. The mission scenario includes the following parts, shown in the preliminary schematic in Fig. 8.
-
Part A: a satellite in a highly elliptical, dipping, high-inclination orbit with a perigee of 150 km and apogee sufficiently high to maintain a mission lifetime above a threshold duration of 1 year and a goal duration of 3 years performs in situ measurements down to 150 km.
-
Part B: the satellite periodically descends to 120 km of altitude at selected passes using an efficient propulsion system, performing measurements for a duration of one or more days and subsequently ascends to the nominal perigee altitude of 150 km. At the lowest perigee altitude the main satellite releases expendable subsatellites.
-
Part C: the subsatellites are equipped with instrumentation such as a combination of accelerometers, magnetometers and ion-neutral mass spectrometers; they complement the main satellite measurements at low altitudes, providing critical two-point estimates that enable the determination of the spatial extent and temporal evolution of key electrodynamics processes below 120 km.
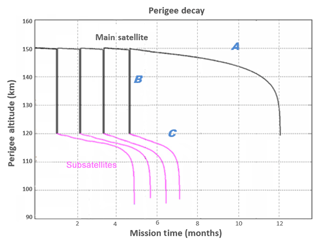
Figure 8Schematic of the main phases of the perigee history for the Daedalus main satellite (gray lines) and four subsatellites (magenta lines). The subsatellites are released during four corresponding descents (“deep dips”) of the main satellite down to 120 km.
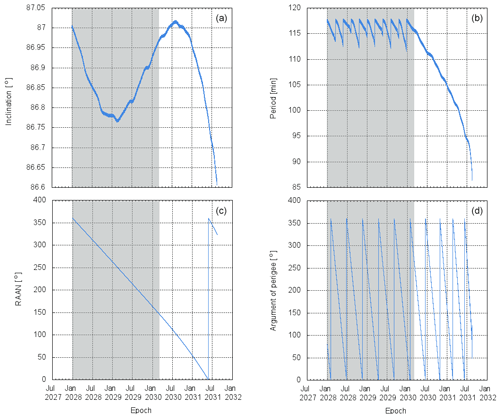
The scenario presented in Fig. 8 is based on a cold gas propulsion system that can provide a lifetime of 1 year; for a more efficient propulsion system, such as a hydrazine propulsion system, the threshold lifetime can be extended to 3 years, and the number of perigee descent campaign maneuvers can be extended. In the following simulations, the baseline maneuver campaign design consists of 10 dips. Each dipping campaign consists of four stages: a lowering perigee maneuver, a propagation of the dipping orbit, a raising perigee maneuver and a post-dip apogee re-boost maneuver. The lowering maneuver is executed in the previous apogee and lowers the perigee altitude from its nominal value of 150 km, to the dipping altitude of 120 km for northern-dipping campaigns and 130 km for southern-dipping campaigns, by thrusting in the ram direction. Then, Daedalus will orbit in this altitude for approximately 11 d. The duration of the dipping campaign depends on the precession of the line of apsides (i.e., precession of argument of perigee, AoP). The precession rate of AoP is at 2.4∘ per day; thus, with a duration of 11 d the perigee will precess over the high-latitude regions where Joule heating and EPP maximize around the auroral latitudes, which is the region of scientific interest for the Daedalus primary science objectives. In this scenario, the dipping campaign starts at a perigee latitude of 75∘; subsequently, perigee precesses almost over the northern pole (maximum latitude 87∘), and the perigee-dipping campaign ends at 75∘ for the northern polar region campaigns (−75 to −87 to −75∘ for the southern polar region campaigns). Subsequently, Daedalus will thrust in the anti-ram in order to raise its perigee back to the nominal value of 150 km. Another maneuver for re-boosting the apogee altitude back to 3000 km will follow. This technique will extend the orbital lifetime of the spacecraft by counteracting the natural decay of the apogee altitude due to drag. The perigee and apogee histories are presented in Fig. 9. The gray-shaded area in Fig. 9 is shown in more detail in Fig. 10. The secular descending trend is due to atmospheric drag, while the short-term and long-term perturbations are mostly due to the nonspherical Earth with much smaller contributions by the gravity fields of the Sun, Moon and Jupiter. A prime mission of 2-year duration is achieved, followed by a 1-year natural decay period, leading to a minimum 3-year lifetime. Based on the above orbital design, the coverage of Daedalus over the baseline lifetime of 3 years is shown in Fig. 11 in terms of magnetic local time. As the coverage is highly dependent on the orbit inclination, simulations for several different inclinations were run: in panels (1a) and (2a) coverage for an inclination of 80∘ is shown; this simulation has an extensive coverage in terms of local time throughout the lifetime of the mission (3 years). In panels (1b) and (2b) coverage for an inclination of 83∘ is shown, whereas in panels (1c) and (2c) coverage for an inclination of 87∘ is shown, with a smaller resulting coverage in terms of local time. Thus, the optimal inclination will need to be decided through a trade-off between the requirements for coverage of high latitudes vs. the requirements for local time coverage; this trade-off will be conducted in the definition phases of the Daedalus mission.
4.2 Instrumentation
In the following we provide the details and requirements of the instruments that are proposed in order to address the scientific objectives of Daedalus.
4.2.1 Ion Drift Meter (IDM) and Retarding Potential Analyzer (RPA) or Thermal Ion Imager (TII)
Ion drifts are needed to separate neutral wind dynamics from plasma motions in order to study Joule heating in the high-latitude LTI and to investigate the E-region and F-region dynamos at low latitudes. For Daedalus, the following options are considered: an ion drift meter (IDM) combined with a retarding potential analyzer (RPA) or a thermal ion imager (TII).
Description of the IDM. For the Ion Drift Meter (IDM), two sensors will be employed to directly derive the ion drift velocity: a retarding potential analyzer (RPA) to measure the plasma energy distribution along the sensor look direction and a planar ion drift meter (IDM) to measure the arrival angle of the plasma with respect to the RPA sensor look direction. The RPA will obtain ion temperature, drift velocity and concentration by measuring incident variations in the ion flux. The IDM will be used to obtain the arrival angle of the ions: in a common design, it is divided symmetrically into four equal pie-shaped segments, and it has a square aperture with sides parallel to the pie cuts. Therefore, any off-axis flow of ions results in different currents in the four segments. This permits the transverse components of ion drift velocity to be measured. When the other sensors face along the s/c velocity vector, the measured ion energy spectra can be used to deduce the component of ion drift in that direction. Therefore, together with the RPAs the instrument is able to obtain the complete ion drift vector. The IDM will also control the bias of a plate on the spacecraft's ram side and will measure the plate current. For constant bias the ion density can be estimated with high time resolution. A sweeping Langmuir mode will allow for the measurement of the electron temperature as well. IDMs and RPAs have been widely used for studying ionospheric plasmas, obtaining measurements from high-altitude sounding rockets (Fang and Cheng, 2013), on the Atmosphere Explorers (AEs) and Dynamics Explorers (DEs) (Hanson et al., 1981), on the Communications/Navigation Outage Forecasting System (C/NOFS) (Stoneback et al., 2012), and on Defense Meteorological Satellite Program (DMSP) satellites (Rich and Hairston, 1994).
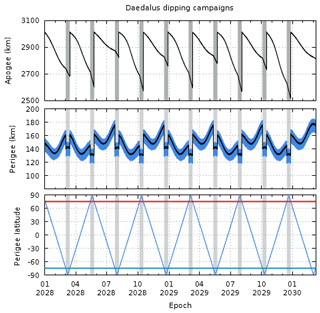
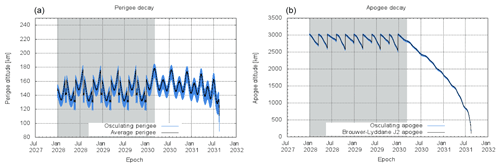
Figure 10Daedalus apogee, perigee and perigee latitude. The times and duration of perigee descents are shown as gray-shaded areas.
Description of the TII. The Thermal Ion Imager (TII) has some heritage from an IDM–RPA but also considerable differences from the IDM–RPA concept in that each of the two TII sensors uses an electrostatic focusing system to produce two-dimensional (angle-energy) images of low-energy ion distribution functions; ions are directed to a micro-channel plate (MCP), from which the signal is amplified and converted to an optical one with a phosphor screen. A charge-coupled device (CCD) camera records 2D images of the ion distribution. Calculating the first and second moments (partially onboard to reduce telemetry requirements) gives the ion drift velocity vector and the ion temperature. For a full 3D distribution two TIIs oriented in orthogonal planes are needed (with redundant measurements in the direction of the s/c velocity). All particles entering the instrument contribute to observed images giving theoretically high sensitivity and good time resolution. TIIs are a relatively new development (e.g., Knudsen et al., 2003) and have been flown on suborbital sounding rockets, on the Canadian e-POP satellite (a version for electrons) and on the ESA Swarm satellites. On Swarm, first moments of 2D images can be obtained at 16 Hz, corresponding to about 500 m spatial resolution. Full 3D ion velocity vectors and (potentially anisotropic) temperatures are provided at 2 Hz (∼3.5 km). As the s/c electric potential significantly affects the measurements, the Swarm TIIs are complemented with Langmuir probes, which also provide the plasma density, eliminating the need for a highly accurate calibration of the total TII particle fluxes. Some of the scientific results that have come from past TII measurements include the characterization of mechanisms responsible for highly localized ion heating cavities (Burchill et al., 2004; Knudsen et al., 2004), observations of ion upflow at speeds of hundreds of meters per second within the polar cusp and cleft (Burchill et al., 2010), and precision measurements of ion demagnetization versus altitude in the collisional lower ionosphere (Sangalli et al., 2009; Burchill et al., 2012). Sangalli et al. (2009) compared TII-measured ion drifts with double-probe electric field and neutral velocity measurements to establish a measurement accuracy better than 20 m s−1 root mean square (RMS).
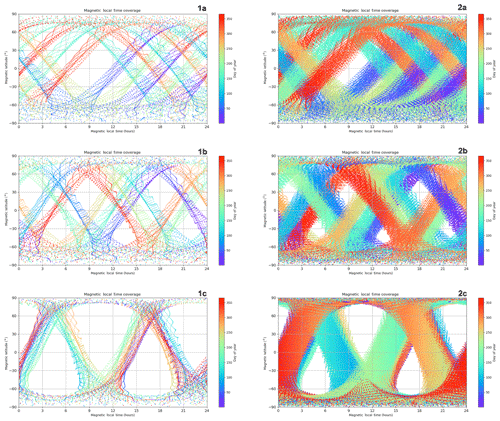
Figure 11Daedalus magnetic local time coverage. Column 1: magnetic latitude and magnetic local time of perigee as a function of the day of year (shown in color) for the entire duration of the mission. Column 2: same as column 1 for all points along the orbit up to 200 km of altitude. Row (a): 80∘ inclination; row (b): 83∘ inclination; row (c): 87∘ inclination.
IDM–RPAs have often been used to also infer the electric field from the ion drifts, assuming that the ambient plasma is strictly subject to an E×B drift; also on Swarm the EFI (electric field instrument) is actually a TII–LP ion drift combo without any direct electric (E) field measurement. Similarly, if the electric fields are measured using a double-probe electric field instrument, then the ion drifts can be calculated under the same assumption. However, that is an assumption that cannot be made safely much below 200 km, as at about 150 km the ion gyrofrequency drops below the ion collision frequency (see, e.g., Kivelson and Russell 1995, Figs. 7.8). For this reason, both an electric field instrument and an ion drift meter are required.
An IDM or TII for Daedalus will need to be able to handle a mixture of molecular ions (, , NO+) and atomic oxygen (O+), at least at lower altitudes below ∼300 km. These are expected to have different ion drifts vi; because of the mass difference, the composition of molecules and O+, and the ion temperature Ti dependence, they could not be derived independently in RPA sweeps, or they could be detected in a TII image at different locations for the same drift and temperature. Instruments on previous missions sometimes separated O+ from H+ and He+, which is easier because of different masses by a factor of ≥4. The mass ratio of molecular ions and O+ is ≈<2. The transition between a plasma dominated by molecular ions and one by O+ occurs between roughly 150 and 250 km of altitude. Also, incoherent scatter radars (ISRs) have problems distinguishing between molecular ions and O+ because of noise in the signals and also because of the relatively small mass difference. A fallback solution is to use a relative composition from a model and fit Ti (ISR) or Ti and vi (in situ ion instrument). It should be noted, however, that models like the IRI-07 do not always give an accurate composition.
4.2.2 Ram Wind Sensor (RWS) and Cross-track Wind Sensor (CWS)
Studies of the kinetics of neutral particle flow in the free molecular flow regime of the satellite environment led early on to various concepts for neutral wind measurements. Based on these concepts, measurements have since resulted in a large body of data of high spatial resolution. These data have revealed an unexpectedly complex and variable neutral atmosphere, a signature of the deposition of large and highly variable quantities of energy. To resolve neutral winds, two sensors will be used on Daedalus: the Ram Wind Sensor (RWS) and Cross-track Wind Sensor (CWS).
Description of the RWS. The Ram Wind Sensor (RWS) will obtain the neutral wind speed along the ram direction of Daedalus by performing a retarding potential energy analysis on an ionized fraction of the flowing neutral gas. In such a configuration the incident ambient ions are electrostatically deflected from the instrument axis so that only the ions produced from the flowing neutral beam have access to the electron multiplier detector.
Description of the CWS. The Cross-track Wind Sensor (CWS) will obtain the cross-track neutral wind velocity by measuring small pressure differences created by the bulk motions of the thermal neutral gas in directions perpendicular to the motion of the satellite. In the design employed by the CINDI instrument onboard C/NOFS (Earle et al., 2007, 2013), the neutral wind instrument included four apertures on a hemispherical cover operated by measuring the arrival angle of the neutral wind at the satellite by detecting small pressure differences between neighboring chambers with orifices pointing in different directions (Hanson et al., 1992). The pressure measured in four cavities behind these apertures was related to the arrival angle of the neutral gas relative to each aperture normal. Combined with detailed knowledge of the spacecraft velocity vector, the pressure differentials between diametrically opposed cavities allowed the cross-track wind speed to be determined in the satellite frame of reference. Ion gauges in each chamber measured currents proportional to the pressure and ionization efficiency of any given neutral species (O'Hanlon, 1989). Both the CWS and the RWS will face in the ram direction. It is noted that uncertainties in the wind velocity measurements can be introduced by small alignment errors during instrument installation on the satellite, such as through pointing errors in satellite attitude control or determination. A second source of error can be introduced due to noise in the instrument electronics; these errors can influence both absolute and relative measurements of velocities in the medium.
4.2.3 Accelerometer (ACC)
The accelerometer onboard Daedalus will measure nongravitational accelerations such as air drag, Earth albedo and solar radiation acting on the satellite. The direct measurement of acceleration α due to air drag can in turn be used to derive the total atmospheric mass density ρ through the fundamental relationship , where Cd, A, m and V are the s/c coefficient of drag, cross-sectional area, mass and velocity, respectively (Hedin, 1991). Accelerometer data can also be used to derive winds in the thermosphere (Sutton et al., 2007; Doornbos et al., 2010; Dhadly et al., 2018). Using expected values of these parameters and obtaining values for ρ from the NRLMSISE-00 atmosphere model, it is calculated that the drag acceleration will be on the order of 10−7g at 500 km and 10−3g at 120 km. This level of dynamic range is easily accomplished with 16 bit analog-to-digital conversion. In order to obtain a spatial resolution of ∼1 km, a sampling frequency of 16 Hz is required for a typical s/c velocity of ∼8 km s−1. A spatial resolution on the order of ∼1 km is sufficient for resolving Joule heating on a scale that can be compared to current models as well as for the detection of gravity waves in the lower thermosphere. Sensitivity of will also allow for the measurement of wind velocities around perigee. Acceptable measurement errors are ±10 % at 500 km and ±2 % at altitudes below 200 km. In addition, there may be a systematic error of up to ±3 % due to drag coefficient uncertainty. The accelerometer measurements will also monitor the thrust of the propulsion system: a sensitivity on the order of to 10−3g is sufficient to accurately capture the orbit adjustments and deep dips of the spacecraft. A typical high-precision accelerometer configuration consists of three single-axis accelerometers mounted mutually at right angles, and the instrument determines the applied acceleration from the electrostatic force required to re-center a proof mass. The output is a digital pulse rate proportional to the applied acceleration.
It is noted that the combination of an accelerometer and reaction wheels of the Attitude and Orbit Control Subsystem (AOCS) of the satellite will introduce restrictions on the usability of the accelerometer, at least for parts of the orbit. As part of the early phases of Daedalus development, these will be further explored. Alternatively, it will also be investigated whether the mass spectrometer of the satellite can be used to derive density with sufficient accuracy for the mission needs.
4.2.4 Energetic Particle Detector Suite (EPDS)
The Daedalus EPDS will consist of three distinct instruments: a High Energy Instrument (HEI), a Low Energy Instrument (LEI) and an Energetic Neutral Atom (ENA) instrument. All three will be mounted to the spacecraft with a clear upward-looking field of view (FoV) that will allow full pitch angle coverage of precipitating particles.
The HEI will provide high-resolution differential energy measurements of relativistic electrons, protons and heavy ions precipitating into the LTI environment, with a pitch angle resolution capable of resolving the distributions of EPP flux within the bounce-loss cone. Electron measurements will be performed in an energy range spanning < 20 keV to > 1 MeV, and proton and heavy ion measurements will be performed from < 20 keV to several tens of megaelectron volts. HEI will be based on a solid-state detector, combining recent advancements in solid-state detector design. The design will need to include detailed modeling of energetic particle–matter interactions, such as GEANT4 simulations, to employ digital signal processing (DSP) and to be able to support advanced real-time characterization algorithms and counting rates up to 106 counts per second. A primary benefit of utilizing DSP is pile-up detection and recovery, making dead time essentially negligible after correction. Examples of existing payloads include the IDEE instrument onboard TARANIS, to be launched in 2019 on a low-Earth orbit (Lefeuvre et al., 2008)
The LEI will consist of an electron sensor and a proton sensor: the LEI electron sensor will provide the 3D velocity distribution (fluxes vs. energy and pitch angle) of thermal and supra-thermal electrons in an energy range spanning < 30 eV to > 30 keV. The LEI proton sensor will provide energy coverage between 30 keV, providing an overlap with HEI useful for instrument cross-calibration, and the ions of a few tens of electron volts. It is noted here that precipitating ions of a few tens of kiloelectron volts can lead to significant enhancements of electron density and conductivities (e.g., Yuan et al., 2014). Heritage electron sensors have already performed measurements at the altitudes of Daedalus on a number of rocket flights and have returned excellent science data. Heritage sensors commonly utilize an electrostatic analyzer to provide measurements of precipitating electrons at high cadence with high energy and pitch angle resolution, enabling the quantification of the energy input into the thermosphere and ionosphere. Electrostatic analyzers are well-understood and have high heritage (Doss et al., 2014), dating back to the original Carlson et al. (1983) top-hat design. Electrostatic analyzers bias the inner of two concentric hemispheres to a positive voltage to select electrons by energy, with high energy and angular resolution ensured by the natural focal properties of the electrostatic analyzer. Electrostatic analyzers count individual particles, typically utilizing micro-channel plate (MCP) detectors with a segmented anode to collect charge pulses and charge-sensitive amplifiers to convert pulses into digital counts. For Daedalus, electrostatic deflectors will be required to increase the FoV to cover at least ∼70 % of the distribution (Sauvaud et al., 2008), including upward-going and downward-going electrons. Upward-going electrons provide information about magnetic and electric fields below the spacecraft and are therefore a secondary science topic. Measurements will need to be made fast enough to resolve spatial structures ∼100 km, requiring 10 s or better cadence. To cover typical supra-thermal electron precipitating fluxes, the sensor will need to be capable of measuring differential energy fluxes of 106–5×109 (cm2 s sr eV)−1 with good statistics in this 10s interval, without saturating.
The ENA instrument will measure neutral atoms in the range from ∼5 to ∼200 keV, which covers the typical range of significant energy density in ENAs generated by charge exchange in the ring current. In common designs, instruments use a thin-window, low-threshold, pixelated solid-state detector (SSD) to measure precipitating ENAs, and the SSD is read out with a low-resource ASIC. Counts can be flexibly accumulated on an instrument field-programmable gate array (FPGA) to match the science requirements. Electrostatic deflection will need to be used to sweep low-energy charged particles out of the instrument field of view. The pixelated SSD will allow for coarse imaging of the ENA flux as well as refined separation of ENAs from energetic charged particles.
4.2.5 Ion Mass Spectrometer (IMS) and Neutral Mass Spectrometer (NMS)
The IMS and NMS instruments will measure the composition and density of the main ion and neutral species along the spacecraft orbit, more specifically of ion species H+, He+, N+, O+, NO+ and as well as neutral species H, He, N, O, N2, NO and O2 (and desirably CO2) in the altitude range ∼100 km to > 500 km. The threshold mass resolution M ∕ dM is ∼30, driven by the requirement to separate between NO and O2. The target mass range is driven by the heaviest species; a mass range of ∼>40 is adequate to resolve up to argon with margin. It is noted here that the spacecraft propellant will need to be selected so as not to interfere with NMS measurements. Regarding the dynamic ranges, as can be seen from Fig. 4 the altitude ranges from 100 to 500 km correspond to density variations from ∼102 to 107 cm−3 for the ions, from ∼104 to 1013 cm−3 for the neutrals, and temperature variations from 200 to 2000 K. Furthermore, cross-track and along-track ion drift and neutral wind velocities can vary in the range of and ±1 km s−1, respectively. Because of the relatively cold temperatures, the thermal velocities of the various particle species (e.g., 1.8–5.7 km s−1 for H, 0.9–2.86 km s−1 for O, 0.64–2 km s−1 for O2) are significantly smaller than the spacecraft velocity of ∼8 km s−1 and on the same order of magnitude as the ion drift and neutral wind speeds. As a result, the various ion and neutral particle velocity distributions will appear like beams (i.e., wider for high-temperature light species and narrower for low-temperature heavy species) on the spacecraft frame of reference. The bulk peak energies vary proportionally to V2 with V in the range 4–12 km s−1 for ions and 7–9 km s−1 for neutrals (0.08–0.75 eV for H+, 0.26–0.42 eV for H, 2.5–24 eV for , 8.3–13.5 eV for O2); the bulk beam angle with respect to the spacecraft ram vector varies in the range ±26.5∘ for ions and ±7.1∘ for neutrals. To adequately capture the distributions the IMS and INS should be designed with an FoV of ±75∘ for ions and ±21∘ for the neutrals as well as for an energy range up to 0–35 eV. Therefore, the particle flux measurements of each species on the spacecraft frame of reference as a function of the look direction in polar coordinates (θ,ϕ) can be written as (A, Ni,n, Ti,n, Ei,n, Vi,n, Vs∕c, Atts∕c), where A is the instrument aperture area, Ni,n, Ti,n and Ei,n are the density, temperature and energy for each ion-neutral species, and Vi,n, Vs∕c and Atts∕c are the vectors for the ion-drift-neutral wind velocities, the spacecraft velocity and spacecraft attitude. Because of the frequent collisions at low altitudes the particle distributions for each species can be well-approximated as Maxwellian distributions (in the general case with kappa distributions) drifted at the vector sum velocity of . With a multi-parameter fit of the flux measurements and minimizing the least mean square error, one can get the total solution for the density of the various ion and neutral densities Ni,n, temperatures, and the ion drifts and neutral winds. Because of redundancy, the proposed IMS–INS suit will emphasize in the mass analysis and sampling the relative densities of each species, taking as inputs the ion-neutral temperatures and drift–wind vector measurements from the dedicated IDM–RPA and CWS–RWS instruments.
The proposed mass spectrometer method is based on electronically gated time of flight (ToF), in which an acceleration voltage of few hundred volts energizes all particles to about the same energy and orders the velocity of all the ions according to the square root of their mass. An electric gate controls the flow of particles from the gate to the detector. The mass of the particles is determined from the ToF measurement at the particle energy. Unlike usual plasma mass analyzers based on foils, the gated ToF method is nondestructive and therefore well-suited for molecular species. Contrary to other methods that scan the mass spectrum (quadrupole mass spectrometers), the ToF method measures all particles simultaneously, a key capability for fast sampling in the transition regions. Also, most importantly, the electronic gating allows for the control of the geometric factor and boosting the detector bandwidth by several orders of magnitude beyond the continuous detector capability of ∼107 cps. This feature enables handling the neutral density dynamic range of ∼1010 and the sampling requirement of ≥16 samples per second. The heritage of gated ToF IMS and NMS includes instruments flown onboard the ExoCube mission (launched in January 2015 in high-inclination LEO) and the Dellingr mission deployed in November 2017 from the ISS (Paschalidis et al., 2014; Klenzing et al., 2018).
In a common design, the core sensor consists of a top-hat electrostatic analyzer surrounded outwards by a circular gate, an RPA, a collimator and deflectors; thus, the sensor can intrinsically cover the entire 4 pi sky with the deflector scanning. However, for the main satellite the FoV will be limited to ±90∘ azimuth and ±75∘ elevation scanning, and the IMS will be performing mass analysis for each look direction. Although the angular imaging will be redundant to the IDM, it can be useful in areas of low densities where IDMs are limited in sensitivity. In addition, although the RPA feature of the IMS will be redundant to the dedicated RPA instrument, the IMS–RPA can be used to block low energies and conduct mass analysis on the nonthermal tail of the ion distributions. Without the elevation and RPA scanning the IMS performs mass analysis in each azimuth direction. Thus, the IMS will do faster relative density sampling of each species, and the dedicated IDM–RPA instruments could be used for calibrating for total density, temperature, and in-track and cross-track ion drifts.
It should also be noted that the best orientation of the IMS and NMS instruments will be with the long FoV (azimuth) on the horizontal plane and perpendicular to the ram direction in order to match the larger horizontal ion drift and neutral winds compared to vertical. This orientation will reduce or eliminate the vertical scanning (elevation) and thus simplify the instrument design.
4.2.6 Electric Field Instrument (EFI)
The Daedalus Electric Field Instrument (EFI) will be designed to make high-accuracy measurements of in situ electric fields, spacecraft surface potential and plasma density. The arrangement of six spherical probes mounted near the tips of six deployable stacer booms will enable 3D in situ measurements using the well-established double-probe technique (e.g., Mozer, 2016). Boom orientation will be such as to minimize interference due to the spacecraft plasma wake (e.g., Cully et al., 2007), as shown in Fig. 12, and to minimize optical shadowing of probe surfaces by the spacecraft body and its protrusions. Each probe will also measure electric potential relative to the s/c. The probes will be current-biased to ensure steady plasma sheath resistance and therefore steady instrument gain at low frequencies (Bale et al., 2008). In the Daedalus plasma environment (120 to 500 km), rigid booms of lengths >∼4 m place the probes many Debye lengths from the s/c, minimizing errors due to s/c surface potential inhomogeneity. A voltage-biased “stub” element will mechanically support each probe and provide electrical isolation from the booms. Each probe will contain a low-noise, high-impedance preamplifier able to pass signals to the s/c. With 8.2 m probe separation, electric fields up to ∼3.6 V m−1 can be measured. This range is sufficient to measure geophysical electric field variations on top of the electric field induced by spacecraft motion (up to ∼450 mV m−1 near perigee). The high oxygen density in the Daedalus orbital environment, in particular near perigee, will cause EFI probe surfaces to oxidize. Oxidation of probe surfaces can create an electrically resistive layer on the probe surface (Ergun et al., 2015), or it can erode probe coatings entirely (Visentine, 1983; Visentine et al., 1985). Either effect can degrade or destroy the ability of EFI to measure DC-coupled electric fields (Mozer et al., 2016). EFI probe coatings will need to be selected so as to mitigate the effects of oxidation to maintain instrument performance. In the double-probe technique, signals from the probes are passed to the EFI electronics box (EB), where they undergo analog processing, including amplification and filtering. The EB will also contain components for driving probe and stub biases and possibly electronics to support a relaxation sounder. All science signals will be digitized by analog-to-digital converters (ADCs) and will undergo digital processing. Digital algorithms will produce time-series waveform and spectral data products with a wide range of selectable cadences. The EFI may also include a relaxation sounder to measure the local plasma density with high accuracy (Trotignon et al., 2003; Andersson et al., 2015). Alternatively, a mutual impedance probe (MIP) or a Langmuir probe (LP) will be considered, both of which are capable of measuring the local plasma density as well as temperature.
The EFI design as proposed to the ESA has the following heritage: preamplifier designs for EFI instruments have strong heritage. The proposed stacer booms have direct heritage from the French DEMETER mission (Parrot, 2002). The preamplifier design has strong heritage from MMS/FIELDS/ADP (Ergun et al., 2016), while the EFI signal-processing heritage includes THEMIS/EFI (Cully et al., 2008), Van Allen Probes/EFW (Wygant et al., 2013), MAVEN/LPW (Andersson et al., 2015), MMS/FIELDS (Ergun et al., 2016) and Parker Solar Probe/FIELDS (Malaspina et al., 2016). The relaxation sounder has direct heritage to MAVEN/LPW (Andersson et al., 2015), whereas the MIP would inherit from the Rosetta/RPC (Trotignon et al., 2007). In each case, the antenna geometry and frequency range should be adapted appropriately for the Earth's ionosphere. Other heritage electric field instruments include those flown onto ISEE3 (Scarf et al., 1978) and Cluster.
4.2.7 Magnetometer (MAG)
High-precision measurements of in situ magnetic fields are crucial for Joule heating estimates, deriving current structures in the ionosphere, and studying and interpreting EPP fluxes and magnetosphere–ionosphere current systems. The Daedalus magnetometers will measure DC magnetic fields. DC magnetic field measurements are a required measurement in Eqs. (10) and (14) of Joule heating, Eq. (15) of Pedersen conductivity, and Eq. (22) of ion-neutral collision frequency; they are also needed for determining the pitch angles of precipitating charged particles, as measured by the EPDS. DC magnetic field measurements also allow for a quantitative determination of the upward and downward currents traversed by the instrument: there are well-established methods for extracting current measurements from in situ magnetometer data (e.g., Ritter and Lühr, 2006; Ganushkina et al., 2015), but they all rely on a priori assumptions about the structure of the currents. For example, the horizontal cross-track component of the current is assumed to be homogenous in the vicinity of the satellite. However, as has been demonstrated in several earlier studies (e.g., Wang et al., 2006; Laundal et al., 2016; Zhou and Lühr, 2017), current estimates from single-satellite data are also essential for the investigation of the space environment.
Heritage high-precision magnetometers include the vector field magnetometer developed by DTU Space, National Space Institute of Denmark, a fluxgate magnetometer developed by the Institut für Geophysik und extraterrestrische Physik of the Technische Universität Braunschweig (Auster et al., 2007, 2008, 2010), a scalar magnetometer developed by the Space Research Institute of the Austrian Academy of Sciences and the Institute of Experimental Physics of the Graz University of Technology, and an absolute scalar magnetometer developed by the National Centre for Space Studies and the French Atomic Energy and Alternative Energies Commission/Electronics and Information Technology Laboratory (Léger et al., 2015; Fratter et al., 2016). All these magnetometers have been used or are currently deployed in different satellite missions and will ensure the 50 Hz or higher measurement frequency of the magnetic field with accuracy and cleanness less than 2 and 0.1 nT, respectively. To achieve these parameters the magnetometers might have to be deployed on a boom, with a length between 0.5 and 2 m; simulations are necessary to determine the exact length through a trade-off between the stability of the satellite and the accuracy of the measurements.
4.2.8 Global navigation satellite system receiver (GNSS)
Global navigation satellite system (GNSS) receivers, while providing orbital position information, are also commonly used for ionospheric tomography and total electron content (TEC) measurements. The underlying principle in this technique is that the ionosphere, being a weakly ionized plasma or gas, affects the propagation of GNSS radio signals. In order to quantify the propagation effects on a radio wave traveling through the ionosphere the refractive index of the ionosphere must be specified. The refractive index of the ionosphere, n, is given by the Appleton and Hartree equation; taking into account that the electron gyro frequency is typically 1.5 MHz, the plasma frequency rarely exceeds 20 MHz and the collision frequency is approximately 104 Hz, the refractive index of the ionosphere can be approximated as n=1–40.3N∕f2 to an accuracy better than 1 % (Klobuchar, 1996), where N is the electron density and f is the system operation (Hz). Subsequently, knowing the refractive index of the ionosphere, it is possible to derive the total number of electrons in the ionosphere, the parameter of the ionosphere that produces most of the changes on the GNSS signal along the GNSS signal trajectory from each satellite to the observer. Slant TEC (STEC) can be estimated as the integrated electron density in a 1 m−2 cross section column along the signal transmission path. STEC can be converted to the vertical TEC (VTEC) by applying a mapping function (e.g., Park et al., 2017, and references therein) that removes the dependency from the elevation angle of the ray path. Daedalus will provide STEC data, which can be translated during post-processing to equivalent VTEC. Regarding GNSS-derived TEC products, Daedalus will build on the heritage from Swarm (Park et al., 2017), CHAMP (Heise et al., 2002), GRACE and COSMIC (Alizadeh et al., 2011). The GNSS receiver will also be used for attitude knowledge.
4.2.9 Subsatellite instrumentation
The proposed Daedalus mission concept includes expendable small subsatellites, potentially in the form of CubeSats, that are released from the main satellite. The subsatellites are released during the main satellite's perigee descent to lower altitudes, and, after the main satellite ascends to higher perigee, the subsatellite measurements at lower altitudes provide estimates of the vertical gradients and the temporal evolution of key LTI parameters. Different instrument combinations will be investigated based on existing miniaturized measurement concepts or those under development. The measurement objectives and potential instrumentation are discussed below, including an assessment of their state of development; these will be further investigated during the initial phases of the Daedalus mission definition.
As discussed in Sect. 3.3, Joule heating is expected to maximize in the altitude region around 120 km. As discussed in Sect. 4.1, the main Daedalus spacecraft will be able to estimate Joule heating by measuring E, B, un, Nn, Ne, Ni and Te in situ at these altitudes during the perigee descent campaigns. The main science objective of the deployed subsatellites is to provide measurements that will enable (a) a differentiation between the temporal and spatial effects of the measured parameters while both the main spacecraft and the subsatellite are at 120 km; (b) a second point of measurements at 120 km while the main spacecraft ascends to higher altitudes after the dipping campaign is competed, which will provide estimates of the vertical gradients of Joule heating; and (c) measurements below 120 km as perigee decreases. In the following we discuss the prioritization of context measurements that can be provided by the subsatellites and a preliminary assessment of their feasibility.
Out of the measurements that are required to obtain Joule heating, as discussed above analytically, the electric field at an altitude of 118 km can be about 20 mV m−1 (Kirkwood et al., 1988), while above 200 km they can be of the order of 20–40 mV m−1 (Davies and Lester, 1999). Electric fields vanish below the altitude region where σP maximizes. The exact profile of E between 140 km and the altitude of maximum σP is not known. Since the electric field is introduced into Eq. (14) as squared, it is expected to have a considerable impact if it is not measured properly at low altitudes. Thus, E is a key parameter to measure at a second point below the perigee altitudes of the main satellite, at altitudes of maximum σP. Neutral density, Nn, and neutral wind velocity, un, vary significantly between the 140 km region and the region where σP maximizes (e.g., Cai et al., 2013); Nn affects the collision frequencies, and un is directly related to qj. The consequences for the overall estimation of the Joule heating are thus also considered to be considerable. Electron density, Ne , and ion density, Ni, can reasonably be assumed to be the same in this region. They can vary noticeably between 140 km and altitudes of maximum σP (up to a factor of 2–5 based on TRANSCAR simulations; see, e.g., Blelly et al., 2005). Since these parameters go to the collision frequency estimation, which is also a function of Nn, their role cannot be neglected, but maybe they are of secondary importance compared to E, Nn and un for Joule heating estimations. However, their role is significant as a proxy for EPP estimations, and simultaneous measurements of Ne at different altitudes along the same orbit (even with the implications of the phase difference between the two satellites, as described in Sect. 4.3.5) can provide significant improvements to models that have been used as a proxy for EPP by improving the assumptions made therein (see, e.g., Rees, 1963; Schunk and Nagy, 2004; Semeter and Kamalabadi, 2005). Furthermore, in situ measurements of Ne would also be relevant for studying ionization and the energy input by solar EUV. For example, Lin and Chu (2017) recently performed an extensive modeling but could only compare to the ∼40-year-old AE-C data, which reached down to 135 km. The combination of Ne from the main satellite at 150 km perigee and the subsatellite at 120 km perigee would provide a novel dataset from which to improve such modeling. Finally, measurement of the magnetic field, B, is important for Joule heating estimations but not critical, as models of the magnetic field at these altitudes are considered to have high fidelity. In the following we discuss the maturity of miniaturized instrumentation for the above parameters.
The technology for nanosatellites based on the CubeSat paradigm is advancing at a very rapid speed. With much improved capabilities and reliability over the last decade has also followed the demonstration of the utility of CubeSat-based missions for a broad range of applications (see, e.g., Zurbuchen et al., 2017). Consolidation of the observational requirements will also dictate the observational requirements for the subsatellites, and further analysis and prioritization of the science questions will determine for which parameters the extended lower-altitude coverage is most essential and can be supplied by a CubeSat. Currently, most, but not quite all, of the above listed parameters have well-proven instrument solutions. Based on currently demonstrated capabilities and new capabilities that are in an advanced state of development, the feasibility of achieving the measurements required for Daedalus from a CubeSat-based platform is summarized in Table 3, including a classification in terms of expected advancement by the time of the Daedalus launch, the names of corresponding missions and references pointing to the status of development.
Table 3List of potential instruments for subsatellite platforms, including a preliminary assessment of feasibility and the missions that have flown the corresponding instruments.
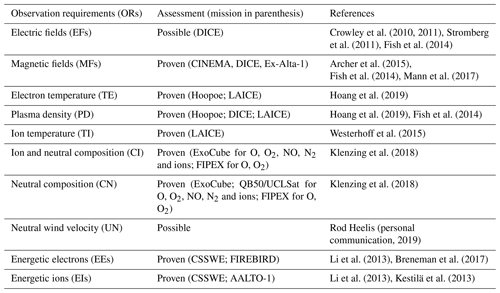
In this table it can be seen that, in particular, measurements of Ne, Nn, Ti, and the composition of ion and neutral species, as well as measurements of the magnetic field, all have proven or well-advanced development solutions for miniaturized platforms, including CubeSats. Regarding electric fields, an instrument based on the double-probe technique has been developed for a multi-satellite mission concept and is likely to be demonstrated within the timeframe of the development of Daedalus (e.g., Crowley et al., 2015). Recent developments in the miniaturization of neutral wind instruments indicate that un measurements are also likely to be enabled onboard CubeSat platforms in the near future (Rod Heelis, personal communication, 2019). These measurements therefore constitute high-priority objectives that are considered to be feasible for the Daedalus CubeSats.
Other measurements that can be achieved from miniaturized platforms and corresponding instrumentation include the following: (a) accelerometer and laser retroreflectors (a lightweight, passive instrument designed to reflect laser pulses back to their point of origin on Earth) can be employed to determine atmospheric density. This will allow for the resolution of the time constant for density increases at lower altitudes after a solar storm and the vertical extent of the density changes due to Joule heating. (b) A miniaturized ion-neutral mass spectrometer (INMS) can provide composition measurements of the primary constituents at lower altitudes; this will allow for the resolution of the altitude profile of key constituents, while being able to cross-calibrate the INMS on the main satellite and the subsatellite. (c) Miniaturized energetic particle instruments determine EPP at lower altitudes and provide the altitude distribution of particle precipitation. (d) There have been recent efforts to combine IDM and RPA instrument functionality into one lightweight, small, low-power unit ideal for small satellites, including CubeSats (Hatch, 2016; Swenson, 2017); testing has shown that the design, while saving on power and space, does not compromise much in terms of instrument accuracy relative to using two separate instruments. The combination of an RPA–IDM on the main satellite and on a second point down below would allow for the determination of the altitude distribution of ion drifts. Another example includes the Advanced Ionospheric Probe (AIP), with flight heritage onboard the FORMOSAT-5 satellite (Lin et al., 2017); the AIP is an all-in-one plasma sensor that measures ionospheric plasma concentrations, velocities and temperatures. (e) Finally, the subsatellites can carry a radio occultation measurement device, sending signals to the mother ship. The signals from the radio occultation device can be used to determine the density in the vicinity of the mother ship, which makes an in situ measurement.
4.3 Further observational and measurement requirements relevant to the mission concept
In the following, we provide further details of the observational and measurement requirements placed on the Daedalus mission concept in terms of the observation geometry and placement of the instruments, the observing scheme of the main satellite combined with the subsatellites, spatial and temporal coverage and resolution, and a preliminary assessment of accuracy requirements; these will be further consolidated during the first phases of the Daedalus mission definition.
4.3.1 Observation geometry
The following key scientific instrumentation needs to be placed in the Daedalus spacecraft ram direction: IDM–RPA (or TII), IMS–NMS and RWS–CWS. Three-axis stabilization is required with stringent attitude control and pointing knowledge requirements. The need to perform in situ measurements in the LTI is best realized by a spacecraft with minimal cross section and body-mounted solar panels to minimize drag effects. A preliminary design of Daedalus with extended electric field booms and an overview of the instrumentation that needs to be placed in the ram direction of the spacecraft, thus defining the minimum cross section, is shown in Fig. 12.
4.3.2 Observing scheme
Daedalus will perform episodic descents to lower altitudes during times of varying solar wind conditions to parameterize the response of the LTI to external driving. Initially the episodic descents will be planned during quiet times, when thermosphere density and satellite drag are lower; subsequent descents will be performed during active times, planned based on space weather predictions. Descents can be performed in a stepwise manner in order to perform measurements at different perigee altitudes and also to ensure safe descents as well as to avoid excessive loss of spacecraft velocity due to unexpectedly high satellite drag. An overview of the observing scheme through the complex high-latitude current system is given in Fig. 13, which for illustrative purposes describes ionospheric currents as two-dimensional sheet currents, while in reality the currents are three-dimensional with existing speculation as to how the currents are closed (Amm et al., 2011). The orbits of the main satellite (green) and a subsatellite (red) are shown both for the mission phase when perigee is at high latitudes (solid lines), when the satellite can perform in situ measurements in the region where Joule heating maximizes, and also at times when apogee is at high latitudes due to the precession of the orbit's perigee (dashed lines), when vertical gradients of field-aligned currents and EPP can be investigated. Schematic locations of the Pedersen, Hall and field-aligned currents are also drawn. Several mission scenarios can be executed: if a subsatellite is released in association with a solar storm then one can look at the time history during and after the storm. By quantifying Joule heating in situ and by monitoring the density enhancements and composition changes at various altitudes below, Daedalus will allow estimates of the extent and distribution of the Joule heating region to be made and enable the calculation of the total energy deposition during the storm. Further, Daedalus can contribute to current closure speculations in unprecedented ways through its mother–CubeSat combination. When the perigee is at low latitudes, dynamo mechanisms can be studied with two-point observations, ideally with one point in the E-region and one point in the F-region, such that the actual creation of the dynamo can be observed at low altitudes and the effects of the dynamo mechanism can be observed at high altitudes. Daedalus can also test theoretical explanations for the equatorial anomaly (Appleton, 1946), which has not been measured in situ before with multipoint measurements.
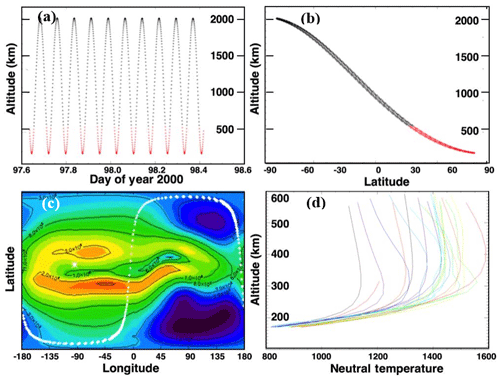
Figure 14(a) Altitude vs. time for 10 Daedalus orbits; (b) altitude vs. latitude. Red dots: measurements below 500 km. (c) Horizontal sampling and (d) vertical sampling of neutral temperature from NRLMSISE along 10 consecutive orbits during the April 2000 storm.
4.3.3 Spatial coverage and spatial resolution
The region of interest for the primary science objectives is from 100 to 200 km; however, measurements will be performed from altitudes of 500 km and downwards in order to provide context measurements and to cover the entire range in which Joule heating and other energy transport processes take place. The latitude and altitude coverage of Daedalus throughout its mission lifetime is presented in Fig. 15. As shown in this figure, Daedalus will focus primarily on high latitudes (> 75∘), where perigee will be lowered to 120 km, but will also gather data at middle and low latitudes at its nominal perigee altitude of 150 km. The upper limit of 500 km is set due to limitations in the maximum dynamic range that the IMS and NMS can achieve, but it can be extended upwards on a per instrument basis in order to allow for conjunctions with other missions at higher circular orbits and/or the investigation of phenomena that extend to higher altitudes. Instruments such as EFI, MAG and EPDS can operate along the entire orbit to allow additional science objectives to be addressed. An example of the relation between spatial resolution and temporal resolution is given in Fig. 14, obtained through sampling the NRLMSISE-00 model along the simulated orbit.
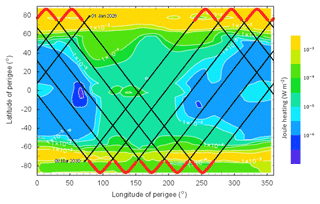
Figure 16Perigee location history for nominal perigee altitudes of 150 km are shown in black; perigee descents to lower altitudes of 120 km are shown in red. In the background, a simulation of height-integrated Joule heating derived from the TIE-GCM is shown. Color indicates the height–integrated Joule heating (units: W m−2).
Regarding the latitude–longitude coverage, it is preferable to keep perigee at as high a latitude as possible, which is a trade-off in the ellipticity of the orbit: the more elliptical the orbit, the less the perigee precesses. However, the more elliptical the orbit, the longer the orbital period becomes and thus the more the revisit time at perigee suffers. Finally, perigee precession allows measurements at both at high and low latitudes to be performed, thus allowing for measurements of Joule heating and EPP at high latitudes and also the equatorial electrojets at equatorial latitudes. The perigee precession of Daedalus throughout its lifetime is presented in Fig. 16. Simulations of Joule heating are shown in the background, as derived from simulations using the TIE-GCM. At northern high latitudes Daedalus dipping campaigns cover the region where Joule heating maximizes, whereas at southern latitudes Daedalus misses the region of maximum Joule heating by approximately 10∘. The exact regions of perigee dips will be determined through a trade-off analysis that takes into account the prioritized science objectives, measurement requirements and desired mission lifetime; a preliminary example of the long-term evolution of the Daedalus argument of perigee, inclination, right ascension of the ascending node and eccentricity for the sample orbit in Fig. 9 is shown in Fig. 17.
4.3.4 Temporal coverage and temporal resolution
The temporal coverage needs to be reconcilable with the spatial and temporal scales of the phenomena under investigation. In general, the thermosphere and ionosphere have a response and relaxation time on the order of days. At low latitudes the dynamics are a diurnal phenomenon, but one that can change every day. The measurement strategy of Daedalus will be to measure all local times with a precessing satellite. At middle and high latitudes dynamic timescales are on the order of hours: for example, Joule heating happens over the course of several hours. During a large storm, the dynamic timescale is days. This, in turn, defines the timescale required for the repeat cycle. In the mission concept described herein, the main spacecraft has an orbital period of ∼120 min and will provide the required temporal coverage to identify diurnal variations and the response and relaxation of the LTI to external solar driving. At the same time, the combination of the main spacecraft with subsatellites will provide measurements to separate temporal from spatial effects and will also enhance the repeat cycle of the main satellite with context measurements. Regarding temporal resolution, all instrument signals will be recorded below 500 km at ≥16 samples per second, giving a horizontal resolution ≤1 km. Brief segments will be recorded for later playback as “burst” data, especially during the deep dips of the spacecraft, or other selected time intervals.
It is noted that the subsatellites will be released at a lower perigee and they will have a different cross-section-over-mass ratio than the main satellite as well as different drag coefficients; thus, they will be flying at slightly different velocities than the main satellite. This means that measurements at two different altitudes over the same latitude and local time will have a temporal offset that will increase as the satellites drift apart. The maximum temporal offset for the coregistration of measurements by the main satellite and the subsatellite will be equal to half the orbital period, or ∼58 min. However, the timescales of events under investigation are on the order of several hours to days; thus, the maximum temporal offset between the measurements at the two altitudes is acceptable and provides important information for the spatial and altitude scale of events in the LTI. Regarding the aforementioned coverage-related issues, simulations of conjunctions of the main satellite with the released subsatellite were performed. After the release of the subsatellite and the execution of the dip-out maneuver of the main satellite, Daedalus will orbit at its nominal perigee of 150 km and the subsatellite will follow a similar orbit at a lower perigee altitude of 120 km. As the subsatellite will have a shorter orbital period, the two satellites will be in and out of phase periodically, as shown in Fig. 18a. For the simulated scenario the expected lifetime of the subsatellite was calculated at 26 d, which corresponds to 314 orbits of the main spacecraft; thus, the subsatellite will cross the main spacecraft's perigee latitude and subsequently the main spacecraft will follow with a temporal offset in the range of 0–58 min. Temporal offsets were binned in windows of 5 min, and the total number of orbital conjunctions over similar perigee latitudes was estimated in order to quantify the temporal offsets with which the main satellite and the subsatellites will be able to provide altitude gradients. The results are presented in Fig. 18b. It is noted that, as demonstrated in Fig. 2, during storm-time conditions, increases in Joule heating by a factor up to 4 can be observed within a 60 min period. Thus, temporal separations of a fraction of this period could meet the assumption of semi-simultaneous observations. As Fig. 18b demonstrates, there will be a significant number of orbits in the temporal offset window of < 10 min (76 orbits). However, this is dependent on the condition that the dipping maneuver and the subsequent release of a subsatellite can be synchronized to occur during a storm-time event. This leads to additional requirements for the mission in terms of the minimum lead time for the performance of a dipping maneuver and the release of a subsatellite, which will be investigated in the course of the upcoming phases of the proposed mission.
4.3.5 Measurement accuracy requirements
To address the primary science objectives of Daedalus, in particular the determination of Joule heating, precise vector neutral wind and ion drift measurements are required. The most stringent stability and alignment requirements are dictated by the IDM and the neutral wind sensors (RWS and CWS). The IDM needs to be constantly pointing towards the direction of travel of the spacecraft (ram direction), and thus three-axis stabilization is required. Three-axis stabilization is also ideal for particle measurements. Thus, the spacecraft should be aligned so that the first axis always points towards the ram direction (horizontal axis), the second axis points towards the center of the Earth (vertical axis) and the third axis completes the orthogonal system (horizontal axis). Instruments for ion drift and neutral wind determination commonly have an FoV of ±45∘; this could be aligned in the ram direction, since pointing is generally better known in that direction. A trade-off analysis should be conducted to identify the optimal means to achieve the required alignment; it is noted here that reaction wheels will potentially hinder accelerometer measurements, which are needed for density determination. Errors in pointing knowledge will propagate onto errors in ion and wind speeds; for the Daedalus spacecraft orbit at perigee, 1∘ of error in pointing knowledge corresponds to 140 m s−1 of error in the knowledge of ion drifts and winds. Observation requirements for Joule heating determination lead to an estimated required spacecraft pointing knowledge within 0.02∘ accuracy in the vertical direction (< 3 m s−1 accuracy in ion drift and wind speed) and 0.14∘ accuracy in the horizontal directions (< 20 m s−1 accuracy in ion drift and wind speed); these will be consolidated during the initial phases of the Daedalus mission definition. The attitude pointing itself can be much less accurate, up to 0.5∘. To achieve the above pointing knowledge and alignment, two star cameras are baselined. The pointing that can be kept using an aerodynamic stable satellite design and the sizing of the actuators will depend on the density and wind magnitudes and variability, which are going to be investigated more in depth as part of the Daedalus phase-0 studies. For comparison, the GOCE mission's science operations, in particular the deorbit phase, provide useful information for the behavior of Daedalus while at perigee; a comprehensive analysis of environmental and actuator torques on GOCE during science operations is available in Visser et al. (2018). During science operations as well as much of the deorbit phase, GOCE's attitude control was dominated by magnetic torquer actuators, aided by the satellite's aerodynamically stable design. Using magnetic torquers as the primary actuators was a unique aspect of the GOCE mission (Sechi, 2006). More capable and traditional actuators, such as reaction wheels or cold gas thrusters, were not used on GOCE to keep the gradiometer measurement environment as undisturbed as possible. Only during the final days of deorbit did the aerodynamic torques start to dominate over the magnetic torques. The accuracy of pointing, within ±10∘ of the atmosphere–satellite relative velocity vector, that GOCE exhibited throughout the time it returned data should also be sufficient for the instruments on Daedalus, while at the lowest altitudes, Daedalus might additionally be able to make use of more capable attitude control actuators.
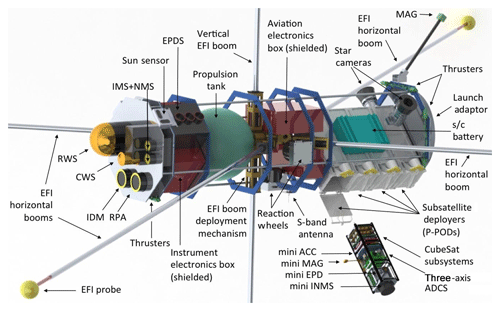
Figure 19Interior of the main Daedalus satellite, including key s∕c subsystems and instrumentation. A deployed CubeSat subsatellite is also shown, with examples of potential subsatellite miniaturized instrumentation.
Other than the pointing attitude and knowledge considerations, it is noted that for many instruments the signal-to-noise ratio will be favorable in the higher-density upper atmosphere than measurements that are currently performed in space. Some upgrading of the instrument performance is anticipated to achieve the higher sampling rates needed in order to sample small-scale variations with a high orbital velocity as expected at the Daedalus perigee locations (∼8 km s−1).
4.4 Spacecraft design constraints and design considerations
The low altitudes that Daedalus targets pose a number of technical challenges. To overcome these challenges, the original design of Daedalus was based on the following criteria and an initial layout with subsystems as shown in Fig. 19.
4.4.1 Spacecraft structure
The structure of the main Daedalus spacecraft should employ an aerodynamic design to compensate for increased drag during perigee passes at low altitudes. The minimum cross section is determined by the ram direction instrumentation and by the cross section of the deployed electric field booms. The former should be minimized in collaboration with instrument designers, and the latter should be designed as narrow as possible while maintaining stability and rigidity in the high-drag environment during perigee. The preliminary design has a cross-sectional area of 0.4 m2 for the spacecraft body and a cross section of 0.2 m2 for the stacer booms; if these could be significantly reduced, further increases in the mission lifetime could be realized. The use of special fins or structures should be investigated as part of the Daedalus feasibility studies to increase the aerodynamic stability while minimizing the drag coefficient (Cd) of the main spacecraft.
4.4.2 Spacecraft Stabilization and Attitude and Orbit Control Subsystem (AOCS) considerations
Three-axis stabilization is a measurement requirement for the ram direction instrumentation; two star trackers are baselined herein. Instrument pointing knowledge and pointing control requirements pose restrictions on the AOCS. The AOCS design should take into account modes of vibration of the electric field and magnetic field booms. In addition, the release of the subsatellites and the use of propulsion will cause the spacecraft center of mass to move from its initial position; the use of six (two per axis) mass trim mechanisms, driven on a nut rotor with a stepper motor, would allow the center of gravity of the satellite to be readjusted after deep-dip maneuvers and subsatellite releases.
4.4.3 Propulsion subsystem considerations
The propulsion subsystem should be optimized to maximize the number of designed dipping maneuvers (10 perigee descents are plotted in Fig. 9), while maintaining apogee to extend the mission lifetime. Maximizing the number of dipping maneuvers depends on the total mass of the propellant and also on the propellant's specific impulse (Isp): the latter is a measure of how efficiently a propulsion subsystem uses the propellant, with higher Isp meaning that less propellant mass is needed for a given thrust. In addition, the required time for achieving the desired altitude descent or ascent depends on the thrust capability of the thruster, with higher thrusts corresponding to faster maneuvers. In the presented simulations, a conservative specific impulse of 240 s (hydrazine propellant) and a high-thrust propulsion system of 20 N total thrust were assumed. Commonly, a lower-thrust (∼1 N) system is also used for attitude purposes. One constraint regarding the selection of the propellant is that it should not contain constituents that could contaminate IMS and NMS measurements. Another way of addressing this constraint is to avoid firing the thrusters at the region of interest (perigee region), with the disadvantage of more fuel consumption, as apogee maintenance maneuvers off the perigee need more fuel. Hybrid propulsion systems can be investigated, such as those that have been proposed for the ESCAPE mission (Iannis Dandouras, personal communication, 2019): one could be used for attitude maneuvers, which can be low Isp and relatively low thrust, and a second high-Isp propellant could be used for dipping campaigns. These should be investigated in the early phases of the mission design but are not considered high-risk areas.
4.4.4 Radiation environment considerations
The highly elliptical orbit of the Daedalus mission means that the spacecraft will cross the inner radiation belt during apogee passes. This becomes particularly significant above ∼2250 km. Thus, special measures should be taken to utilize radiation-hardened electronics and/or to shield all critical electronics. Both the main spacecraft and the subsatellites need to be radiation hardened. A radiation monitor will be part of the Daedalus payload in order to assist in safeguarding the spacecraft operations and characterizing the radiation environment.
4.4.5 Spacecraft thermal design
At perigee, in particular during perigee descents, enhanced free molecular heating rates can lead to significant heating of the spacecraft, in particular at the ram direction. Adequate heat shields and an efficient heat dissipation system should be used to mitigate potential overheating of the ram direction instruments. Electric field booms also need to be tested under anticipated thermal and aerodynamic loads (combined) to ensure that they do not buckle or bend.
4.5 Relation to other missions and potential synergies
The Daedalus mission will complement a series of very successful past missions and will also be synergistic with a number of planned and current missions; these are discussed in the following.
4.5.1 Relation to past missions
Several missions have performed in situ measurements in the LTI, demonstrating the feasibility of Daedalus measurements: Swarm is a current ESA EO three-spacecraft constellation mission to study the Earth's magnetic fields and currents flowing in the magnetosphere and ionosphere. Recently, the enhanced Polar Outflow Probe (e-POP) instrument package on Canada's Cassiope satellite was integrated with Swarm as the mission's fourth element. Two of the Swarm satellites fly side by side at 460 km and one at 530 km, and Swarm's fourth element, e-POP, flies in an elliptical polar orbit with a perigee of 325 km and apogee of 1500 km; these are significantly higher than the 100–200 km transition region that is targeted by Daedalus. Swarm measurements include magnetic fields, ion density, ion drift velocity and nongravitational accelerations like air drag, winds, Earth albedo and solar radiation pressure; however, Swarm does not carry an ion or a neutral mass spectrometer, and it also does not differentiate actual ion drifts from E×B ion drifts, which are crucial for the Daedalus science objectives in the LTI region. The Daedalus mission's measurements will help extend to lower altitudes several scientific objectives of the Swarm constellation mission, such as investigating electric currents in the magnetosphere and ionosphere and quantifying the magnetic forcing of the upper atmosphere. MAVEN, an active Mars mission, successfully performs measurements in the Martian thermosphere–ionosphere from a highly elliptical orbit, and the mission scenario also includes deep dips into the lower thermosphere, providing complete coverage of the Martian upper atmosphere and its interactions with the solar wind. Measurements include ion and neutral composition, energetic particles, and electric and magnetic fields, similarly to the Daedalus concept, as well as neutral and ion winds, using the ion and neutral mass spectrometer. C-NOFS targeted the effects of ionospheric activity on signals from communication and navigation satellites. Similarly to Daedalus, it performed in situ measurements of ion and neutral velocities as well as electric fields using six booms from an elliptical orbit; however, it had an equatorial orbit, and its perigee was 405 km, much higher than the altitude range targeted by Daedalus. C-NOFS also lacked composition measurements. Cluster is an ESA mission consisting of four identical spacecraft flying in a tetrahedron-like formation; it was launched in 2000 into an approximately 4×20 RE polar orbit with an inclination of about 87∘ and is still operating. One of the four spacecraft, Tango (Cluster 2), made the lowest dip into the ionosphere in 2009 down to about 200 km of altitude, performing field and ionospheric plasma measurements. In addition to these more recent missions, the Atmosphere Explorers (AEs) of the 1970s and the Dynamics Explorer (DE) mission of the 1980s also performed in situ measurements of density, ion drifts, multiphase (neutral, ion) composition and temperature structure down to the heart of the transition region (e.g., perigee of ∼150 km and deep dips down to ∼130 km by AE-C and down to 280 km by DE). These spacecraft lacked neutral wind measurements, with the exception of DE, which for the first time measured the vertical motions of the local wind. It is also noted that the dynamic range of some of the key measurements of the AEs, such as mass spectrometer composition, made the data interpretation difficult at low altitudes. Remote sensing missions of the LTI include UARS (e.g., the WINDI instrument looked at winds and temperature at low and middle latitudes at 85 to 250 km) and TIMED (which obtained O, O2, N2 and ion density during daytime). These are among the primary sources of information on the LTI; however, for many key processes simultaneous measurements of all key geophysical variables are needed.
4.5.2 Synergy with ground-based instruments
An extensive network of ground-based instruments can provide supplementary context measurements in the ionosphere and be cross-calibrated in situ by Daedalus. These include existing networks of ionosondes, incoherent scatter radars, coherent scatter radars, auroral imagers, photometers and Fabry–Pérot interferometers. In particular, the state-of-the-art volumetric EISCAT_3D radar will be fully operational in 2022, well-timed with a potential launch of Daedalus in 2027–2028, if selected. The radar will provide electron density, electron and ion temperature, and vector ion drift velocity between 70 and 1000 km within a 3D cone with a diameter of 500 km at an altitude of 150 km (McCrea et al., 2015). Together, Daedalus and EISCAT_3D would constitute the “microscope–telescope” approach of combined in situ and remote sensing measurements, providing a powerful tool for LTI studies.
4.5.3 Synergy with rocket flights
Exploration of the LTI by sounding rockets is one of the main sources of in situ measurements of density, temperature, electrodynamics, EPP and the composition of the LTI region. A multitude of sounding rocket observations at various latitudes have been performed through parts of the LTI and at various latitudes, with a strong bias at northern latitudes due to the distribution of permanent rocket ranges and launch facilities around the globe. As a prime example that is directly related to Daedalus science objectives, the JOULE-II rocket (Sangalli et al., 2009) has provided vertical profiles of conductivity and Joule heating. A synergistic measurement by a rocket flight together with a Daedalus overpass while at perigee would enable the investigation of the horizontal extent of the region where Joule heating maximizes, while rocket data would provide the vertical profile, enabling a 3D tomography of Joule heating distribution.
5.1 On the anticipated impact of the scientific advances of Daedalus
The scientific advances anticipated from the mission are directly relevant to a number of societal issues: (1) Daedalus will provide critical information of in situ composition to help address the response of the upper atmosphere to global warming in the lower atmosphere and its role in energy balance processes. (2) Measurements that Daedalus will perform in the LTI are essential for understanding the exosphere and modeling its altitude density profile and its response to space weather events, as all exospheric models use parameters from this region as boundary conditions. (3) Furthermore, during geomagnetic storms and substorms, currents with increased amplitudes close through the LTI, producing enhanced Joule (ohmic) heating (Palmroth et al., 2005; Aikio et al., 2012) and leading to significant enhancements in neutral density, which in turn results in enhanced satellite drag. In particular, accurate estimates of drag experienced by satellites and space debris is increasingly becoming important with the continuously growing human activities in space. (4) Through its novel measurements, Daedalus will provide critical measurements for Joule heating estimates that can be used as anchor points in global circulation models. (5) Space weather effects enhance ionospheric scintillation of global navigation satellite system (GNSS) signals, which severely degrades positional accuracy and affects the performance of radio communications and navigation systems (Xiong et al., 2016); Daedalus will measure in situ plasma parameters that are involved in GNSS signal scintillation. (6) Sudden enhancements in the current system that closes within the LTI induce GICs on the ground, the impact of which on power transformers in electrical power systems has, on occasion, been catastrophic (Pulkkinen et al., 2017); this is considered a threat to technology-based societies should an extreme solar event occur. Daedalus will measure in situ the currents that produce GICs and will thus assist in the accurate modeling of GICs in response to geomagnetic activity. (7) Energetic proton and electron precipitation has a role in mesospheric ozone destruction large enough to be important at the atmospheric and climate level (Andersson et al., 2014). So far it has been difficult to assess the impact of the role due to an insufficient energy spectrum associated with the precipitation. Daedalus will provide the necessary EPP energy spectrum, together with local composition, to directly assess the role of EPP in upper atmosphere chemistry.
Despite its significance for the above societal issues, the LTI region is the least measured and least understood of all atmospheric regions. The continuous and ever-increasing presence of mankind in space and the importance of the behavior of this region for multiple issues related to aerospace technology, such as orbital calculations, vehicle reentry and space debris lifetime, together with its importance in global energy balance processes and in the production of GICs and GNSS scintillations, make its extensive study a pressing need. Daedalus responds to the above societal challenges by providing groundbreaking measurements in a region that has been vastly under-sampled via innovative orbital maneuvers and subsatellite deployments. These observations should be sustained so as to resolve the seasonal variability of key LTI phenomena, as described above, while providing sufficient temporal coverage to resolve the timescales of dynamic events that lead to upper atmosphere heating. Measurements will be synthesized from a set of individual instruments, each of which provides critical parameters towards the science results. Daedalus will also have synergy with many current and future scientific space missions, such as MEME-X, AWE, TRACERS, GOLD, ICON, GDC and DYNAMIC.
5.2 On the uniqueness and complementarity of Daedalus
5.2.1 Uniqueness: other means for addressing the mission requirements
Some of the required parameters can be measured by ground instrumentation, but Joule heating and EPP cannot be derived accurately based on those measurements, as all required parameters must be measured simultaneously at the same location. In particular, neutral density and wind estimations from the ground are very problematic within the 100–200 km altitude range. Optical methods based on Fabry–Pérot interferometers exist for neutral wind, but those require non-cloudy conditions and even then only provide height-averaged measurements from typically one or two specific altitudes (e.g., Oyama et al., 2018). In addition, ground stations are inherently limited to a specific location, whereas a spacecraft will eventually cover all local times and latitudes. The uncertainty in obtaining accurate Joule heating estimates between various methods is demonstrated in Fig. 4, where different methods vary in their estimates by up to 500 % (Palmroth et al., 2005). An in situ mission with all necessary measurements will provide reference points against which different models and methodologies can be validated and the role of neutral dynamics can be quantified.
5.2.2 Complementarity: upper atmosphere activities of other national and international bodies
On 28 June 2017, NASA selected nine proposals under its Explorers Program; of these missions, three are directly related to processes in the upper atmosphere and will complement the science results of Daedalus: MEME-X (Mechanisms of Energetic Mass Ejection – eXplorer) will map the universal physical processes of the lower geospace system that control the mass flux through the upper atmosphere to space, potentially transforming our understanding of how ions leave Earth's atmosphere. AWE (Atmospheric Waves Experiment) will investigate how atmospheric gravity waves impact the transport of energy and momentum from the lower atmosphere, a fundamental question in heliophysics. TRACERS will study interactions between the solar wind and the magnetosphere from an altitude of 750 km, focusing on cusp electrodynamics. The timeframe for the development of these three missions is well-timed with the present EE-10 call, and these missions can offer excellent complementarity with the measurements of Daedalus. Two currently active NASA missions are targeting the thermosphere: GOLD (Global-scale Observations of the Limb and Disk), operated by NASA, explores the upper atmosphere through full-disk UV images of Earth from geostationary orbit, through which scientists can determine the temperature and relative amounts of different chemical elements present in the neutral gases (O and N2), which, in turn, help show how the neutral gases shape characteristics of the ionosphere. GOLD was launched on 25 January 2018. ICON (Ionospheric Connection Explorer) will study the ionosphere and neutral upper atmosphere in conjunction with GOLD: while GOLD flies in geostationary orbit, ICON will fly 560 km above Earth, where it can gather close-up images of this region. ICON was prepared for launch in 2019. Finally, NASA's next science targets, as outlined in the Heliophysics Decadal Survey, include two reference missions: GDC (Geospace Dynamics Constellation), a mission to understand how the atmosphere, ionosphere and magnetosphere are coupled as a system and to understand how this system regulates the response of all geospace to external energy input; and DYNAMIC (Dynamical Neutral Atmosphere–Ionosphere Coupling), a mission targeting the fundamental processes that underlie the transfer of energy and momentum into the ionosphere–thermosphere system and to measure the thermospheric and ionospheric variability that lower atmospheric waves cause at higher altitudes.
These missions highlight a new interest in the last exploration barrier, the LTI. However, none of these missions plan to study in situ the key transition region between 100 and 200 km, where most energy balance processes maximize and where most abrupt variations exist.
5.3 On the degree of innovation and the advancement of EO capabilities of Daedalus
An innovative technology of the Daedalus mission concept is the release on command of subsatellites from a mother ship; this can be used in concepts such as the release on demand of subsatellites for Earth observation, remote sensing, communications or other applications. Another innovation is the performance of orbital maneuvers and perigee descents in combination with an efficient propulsion system for orbital maintenance in order to achieve the lowest perigee achieved up to now by an Earth observation satellite. Daedalus measurements will help advance upper atmosphere modeling: EPP data along the s∕c track will be used to drive ionospheric and thermospheric models such as GLOW (Solomon, 2017) and satellite track models (Emery et al., 1985; Deng et al., 1995; Wu et al., 1996) to calculate ionization, heating and composition changes, which can be compared with observations of thermospheric temperatures. These models can use along-track data to derive the global EPP heating. A comparison with observations of thermospheric temperature can lead to estimates of global Joule heating based on the differences between EPP models and observations. Daedalus data will be assimilated into TIE-GCM and other ionosphere–thermosphere models to provide accurate calculations of global Joule heating and EPP heating. At high latitudes, Daedalus data will be used to build AMIE (Assimilative Mapping of Ionospheric and Electrodynamics) convection maps (Richmond, 1992). Thus, an advancement of EO capabilities is that Daedalus measurements will enable the calibration, assimilation and accurate driving of upper atmosphere models. Daedalus will provide critical information regarding EPP and Joule heating, and it will distinguish between heating sources, something that has not been possible to date.
5.4 Conclusions
The analysis presented above demonstrates that an in situ mission to sample extremely low altitudes in the LTI, such as the Daedalus mission concept, is feasible. These measurements are scarce in the 100–200 km altitude region, resulting in processes that are not well-quantified. The proposed mission concept will offer simultaneous measurements of all key parameters that are needed to accurately quantify Joule heating and energetic particle precipitation in situ. There are limitations that arise primarily due to the extremely low altitudes and that are related to the maximum mission lifetime, coverage, and sampling and revisit time that can be achieved; these require detailed analysis and trade-off studies that need to be conducted in the upcoming phases of the mission.
The Daedalus mission concept is also well-timed with a number of international space missions that aim to measure key properties in the LTI by means of remote sensing; these include the recently selected MEME-x, AWE and TRACERS, the recently launched GOLD, and the soon-to-be-launched ICON mission. NASA's decadal survey includes two reference missions that also target ionosphere–thermosphere processes: GDC and DYNAMIC. Furthermore, the state-of-the-art volumetric EISCAT_3D radar (one of the Large-Scale European Research Infrastructures selected by the European Strategy Forum on Research Infrastructures for the next 20–30 years) will be fully operational in 2022, well-timed with Daedalus, and will provide time series of ionospheric parameters over northern Scandinavia. Daedalus will provide in situ validation and cross-calibration of these parameters and will also enable the extension of these measurements along its orbit. With regard to technical constraints, the Daedalus mission concept builds on a series of very successful missions with features that are similar to those of Daedalus, such as the aerodynamic shape of GOCE and its use of propulsion for orbit maintenance, the innovative Swarm missions with instrumentation of extreme precision and direct relevance to upper atmosphere scientific issues, and the deep dips of MAVEN into the thermosphere of Mars; these missions have successfully demonstrated key technologies for the potential implementation of Daedalus.
The data used to support the findings of this study are available from the corresponding author upon request.
TES prepared the first draft of the paper and coordinated efforts. TES, ERT, MP and EA contributed to the descriptions of the science context, science gaps and preliminary mission concept overview. MP contributed to describing the Joule heating and participated in structuring the paper. ID contributed to the description of the EPDS, IMS and NMS instruments. EA provided an analysis on the overall system space engineering feasibility and carried out the assessment of the proposed instrument suite from resources and performance requirements aspects. SB and ST contributed to the discussion of measurement requirements and the Joule heating estimation methodology. ST performed orbital simulations, performed coverage simulations and contributed to the s/c design. GK contributed to the discussion on TEC and MAG and participated in structuring the paper. DM contributed to the description of the EFI. AJ contributed to the EPDS sections, including the description of the HEI. NP contributed to the description of the IMS and NMS instruments. JH contributed to the description of the LEI portion of the EPDS. JS contributed to the discussion of ENAs and ENA instrumentation. MC contributed input to the description of EPP and the EPDS. TMJ contributed to the section on subsatellite instrumentation. ED contributed to the descriptions of the ACC and GNSS as well as details on the GOCE mission low-altitude operations and observations. IS contributed to investigations and the assessment of environment considerations. PP contributed to the error analysis and error estimations. AA contributed to the relation to other missions and potential synergies. TES, ST, VL and ERT contributed to the descriptions and simulations of observation geometry, preliminary s/c design, orbital design, s/c design constraints, and other design considerations. All authors read and approved the submitted paper.
The authors declare that they have no conflict of interest.
Mark Clilverd would like to acknowledge the National Environment Research Council Highlight Topic grant NE/P10738X/1 (Rad-Sat) and National Environment Research Council grant NE/R016455/1 for funding.
This work has been supported in part by an ESA contract (grant no. 4000127346/19/NL/IA) and DUTH (project no. KE82324). The work of Minna Palmroth is supported by the European Research Council Consolidator (grant no. 682068-PRESTISSIMO) and the Academy of Finland (grant nos. 312351 and 309937). The research was also funded by the National Environment Research Council Highlight Topic (grant no. NE/P10738X, Rad-Sat) and the National Environment Research Council (grant no. NE/R016455/1).
This paper was edited by Ari-Matti Harri and reviewed by two anonymous referees.
Ahn, B. H., Akasofu, S. I., and Kamide, Y.: The Joule heat production rate and the particle energy injection rate as a function of the geomagnetic indices AE and AL, J. Geophys. Res., 88, 6275–6287, 1983.
Aikio, A. T. and Selkälä, A.: Statistical properties of Joule heating rate, electric field and conductances at high latitudes, Ann. Geophys., 27, 2661–2673, https://doi.org/10.5194/angeo-27-2661-2009, 2009.
Aikio, A. T., Cai, L., and Nygrén, T.: Statistical distribution of height-integrated energy exchange rates in the ionosphere, J. Geophys. Res., 117, A10325, https://doi.org/10.1029/2012JA018078, 2012.
Alizadeh, M. M., Schuh, H., Todorova, S., and Schmidt, M.: Global ionosphere maps of VTEC from GNSS, satellite altimetry, and Formosat-3/COSMIC data, J. Geodesy, 85, 975–987, 2011.
Amm, O.: Method of characteristics for calculating ionospheric electrodynamics from multisatellite and ground‐based radar data, J. Geophys. Res., 107, 1270, https://doi.org/10.1029/2001JA005077, 2002.
Amm, O., Fujii, R., Kauristie, K., Aikio, A., Yoshikawa, A., Ieda, A., and Vanhamäki, H.: A statistical investigation of the Cowling channel efficiency in the auroral zone, J. Geophys. Res., 116, A02304, https://doi.org/10.1029/2010JA015988, 2011.
Anderson, B. J., Takahashi, K., and Toth, B. A.: Sensing global Birkeland currents with Iridium engineering magnetometer data, Geophys. Res. Lett., 27, 4045–4048, 2000.
Andersson, L., Ergun, R. E., Delory, G. T., Eriksson, A., Westfall, J., Reed, H., McCauly, J., Summers, D., and Meyers, D.: The Langmuir Probe and Waves (LPW) Instrument for MAVEN, Space Sci. Rev., 195, 173–198, https://doi.org/10.1007/s11214-015-0194-3, 2015.
Andersson, M. E., Verronen, P. T., Rodger, C. J., Clilverd, M. A., and Seppälä, A.: Missing driver in the Sun–Earth connection from energetic electron precipitation impacts mesospheric ozone, Nat. Commun., 5, 5197, https://doi.org/10.1038/ncomms6197, 2014.
Appleton, E. V.: Two anomalies in the ionosphere, Nature, 157, p. 691, 1946.
Archer, M. O., Horbury, T. S., Brown, P., Eastwood, J. P., Oddy, T. M., Whiteside, B. J., and Sample, J. G.: The MAGIC of CINEMA: first in-flight science results from a miniaturised anisotropic magnetoresistive magnetometer. Ann. Geophys, 33, 725–735, https://doi.org/10.5194/angeo-33-725-2015, 2015.
Auster, H. U., Apathy, I., Berghofer, G., Remizov, a., Roll, R., Fornacon, K. H., Glassmeier, K. H., Haerendel, G., Hejja, I., Kuhrt, E., Magnes, W., Moehlmann, D., Motschmann, U., Richter, I., Rosenbauer, H., Russell, C.T., Rustenbach, J., Sauer, K., Schwingenschuh, K., Szemerey, I., and Waesch, R.: ROMAP: Rosetta Magnetometer and Plasma Monitor, Space Sc. Rev., 128, 221–240, https://doi.org/10.1007/s11214-006-9033-x, 2007.
Auster, H. U., Glassmeier, K. H., Magnes, W., Aydogar, O., Baumjohann, W., Constantinescu, D., Fischer, D., Fornacon, K.H., Georgescu, E., Harvey, P., Hillenmaier, O., Kroth, R., Ludlam, M., Narita, Y., Nakamura, R., Okrafka, K., Plaschke, F., Richter, I., Schwarzl, H., Stoll, B., Valavanoglou, A., and Wiedemann, M.: The THEMIS Fluxgate Magnetometer, Space Sci. Rev., 141, 235–264, https://doi.org/10.1007/s11214-008-9365-9, 2008.
Auster, H. U., Richter, I., Glassmeier, K. H., Berghofer, G., Carr, C. M., and Motschmann, U.: Magnetic field investigations during ROSETTA's 2867 Šteins flyby, Plane. Space Sci., 58, 1124–1128, https://doi.org/10.1016/j.pss.2010.01.006, 2010.
Bale, S. D., Ullrich, R., Goetz, K., Alster, N., Cecconi, B., Dekkali, M., Linger, N. R., Macher, W., Manning, R. E., McCauley, J., Monson, S. J., Oswald, T. H., and Pulupa, M.: The Electric Antennas for the STEREO/WAVES Experiment, Space Sci. Rev., 136, 529–547, https://doi.org/10.1007/s11214-007-9251-x, 2008.
Bilitza, D. and Reinisch, B.: International Reference Ionosphere 2007: Improvements and new parameters, J. Adv. Space Res., 42, 599–609, https://doi.org/10.1016/j.asr.2007.07.048, 2008.
Birkeland, K.: The Norwegian Aurora Polaris Expedition 1902–1903, New York and Christiania (now Oslo), edited by: Aschehoug, H. and Company, out-of-print, available at: https://archive.org/details/norwegianaurorap01chririch (last access: 29 March 2020), 1908.
Blelly, P.-L., Lathuillère, C., Emery, B., Lilensten, J., Fontanari, J., and Alcaydé, D.: An extended TRANSCAR model including ionospheric convection: simulation of EISCAT observations using inputs from AMIE, Ann. Geophys., 23, 419–431, https://doi.org/10.5194/angeo-23-419-2005, 2005.
Breneman, A., Crew, A., Sample, J., Klumpar, D., Johnson, A., Agapitov, O., Shumko, M., Turner, D., Santolik, O., Wygant, J., Cattell, C., Thaller, S., Blake, B., Spence, H., and Kletzing, C.: Observations directly linking relativistic electron microbursts to whistler mode chorus: Van Allen Probes and FIREBIRD II: Simultaneous chorus and microbursts, Geophys. Res. Lett., 44, 11265–11272, https://doi.org/10.1002/2017GL075001, 2017.
Buchert, S. C.: Entangled Dynamos and Joule Heating in the Earth's Ionosphere, Ann. Geophys. Discuss., https://doi.org/10.5194/angeo-2019-71, in review, 2019.
Burchill, J. K., Knudsen, D. J., Bock, B. J. J., Pfaff, R. F., Wallis, D. D., Clemmons, J. H., Bounds, S. R., and Stenbaek-Nielsen, H.: Core ion interactions with BB ELF, lower hybrid, and Alfvén waves in the high-latitude topside ionosphere. J. Geophys. Res.. 109, A01219, https://doi.org/10.1029/2003JA010073, 2004.
Burchill, J. K., Knudsen, D. J., Clemmons, J. H., Oksavik, K., Pfaff, R. F., Steigies, C. T., Yau, A. W., and Yeoman, T. K.: Thermal ion upflow in the cusp ionosphere and its dependence on soft electron energy flux, J. Geophys. Res., 115, A05206, https://doi.org/10.1029/2009JA015006, 2010.
Burchill, J. K., Clemmons, J. H., Knudsen, D. J., Larsen, M., Nicolls, M. J., Pfaff, R. F., Rowland, D., and Sangalli, L.: High-latitude E region ionosphere-thermosphere coupling: A comparative study using in situ and incoherent scatter radar observations, J. Geophys. Res., 117, A02301, https://doi.org/10.1029/2011JA017175, 2012.
Cai, L., Aikio, A. T., and Nygrén, T.: Height-dependent energy exchange rates in the high-latitude E region ionosphere, J. Geophys. Res.-Space, 118, 7369–7383, https://doi.org/10.1002/2013JA019195, 2013.
Carlson, C. W., Curtis, D. W., Paschmann, G., and Michael, W.: An instrument for rapidly measuring plasma distribution functions with high resolution, Adv. Space Res., 2, 67–70, 1983.
Chun, F. K., Knipp, D. J., McHarg, M. G., Lu, G., Emery, B. A., Vennerstrom, S., and Troshichev, O. A.: Polar cap index as a proxy for hemispheric Joule heating, Geophys. Res. Lett., 26, 1101–1104, 1999.
Codrescu, M. V., Fuller-Rowell, T. J., and Foster, J. C.: On the importance of E-field variability for Joule heating in the high-latitude thermosphere, Geophys. Res. Lett., 22, 2393–2396, https://doi.org/10.1029/95GL01909, 1995.
Codrescu, M. V., Fuller-Rowell, T. J., Roble, R. G., and Evans, D. S.: Medium energy particle precipitation influences on the mesosphere and lower thermosphere, J. Geophys. Res., 102, 19977–19987, 1997.
Connor, H., Zesta, E., Fedrizzi, M., Shi, Y., Raeder, J., Codrescu, M., and Fuller-Rowell, T.: Modeling the ionosphere-thermosphere response to a geomagnetic storm using physics-based magnetospheric energy input: OpenGGCM-CTIM results, J. Space Weather Space Clim., 6, A25, https://doi.org/10.1051/swsc/2016019, 2016.
Crowley, G., Fish, C., Swenson, C., Burt, R., Neilsen, T., Barjatya, A., Bust, G., and Larsen, M.: Dynamic Ionosphere Cubesat Experiment (DICE), Proceedings of the 24th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 9–12 August, 2010, SSC10-III-7, 2010.
Crowley, G., Fish, C., Swenson, C., Burt, R., Stromberg, E., Neilsen, T., Burr, S., Barjatya, A., Bust, G., and Larsen, M.: Dynamic Ionosphere Cubesat Experiment (DICE), Proceedings of the 25th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 8–11 August, 2011, paper: SSC11-XII-6, 2011.
Cully, C. M., Ergun, R. E., and Eriksson, A. I.: Electrostatic structure around spacecraft in tenuous plasmas, J. Geophys. Res.-Space, 112, A09211, https://doi.org/10.1029/2007JA012269, 2007.
Cully, C. M., Ergun, R. E., Stevens, K., Nammari, A., and Westfall, J.: The THEMIS Digital Fields Board, Space Sci. Rev., 141, 343–355, https://doi.org/10.1007/s11214-008-9417-1, 2008.
Davies, J. A., Yeoman, T. K., Lester, M., and Milan, S. E.: Letter to the Editor: A comparison of F-region ion velocity observations from the EISCAT Svalbard and VHF radars with irregularity drift velocity measurements from the CUTLASS Finland HF radar, Ann. Geophys., 18, 589–594, https://doi.org/10.1007/s00585-000-0589-6, 2000.
Deng, W., Killeen, T. L., Burns, A. G., Johnson, R. M., Emery, B. A., Roble, R. G., Winningham, J. D., and Gary, J. B.: One-dimensional hybrid satellite track model for the Dynamics Explorer 2 (DE 2) satellite, J. Geophys. Res., 100, 1611–1624, 1995.
Dhadly, M. S., Emmert, J. T., Drob, D. P., Conde, M. G., Doornbos, E., Shepherd, G. G., and Ridley, A. J.: Seasonal dependence of geomagnetic active-time northern high-latitude upper thermospheric winds, J. Geophys. Res.-Space, 123, 739–754, https://doi.org/10.1002/2017JA024715, 2018.
Doss, N., Fazakerley, A. N., Mihaljčić, B., Lahiff, A. D., Wilson, R. J., Kataria, D., Rozum, I., Watson, G., and Bogdanova, Y.: In-flight calibration of the Cluster PEACE sensors, Geosci. Instrum. Method. Data Syst., 3, 59–70, https://doi.org/10.5194/gi-3-59-2014, 2014.
Doornbos, E., van den Ijssel, J., Lühr, H., Förster, M., and Koppenwallner, G: Neutral Density and Crosswind Determination from Arbitrarily Oriented Multiaxis Accelerometers on Satellites, J. Spacecraft Rockets, 47, 580–589, https://doi.org/10.2514/1.48114, 2010.
Drob, D. P., Emmert, J. T., Crowley, G., Picone, J. M., Shepherd, G. G., Skinner, W., Hays, P., Niciejewski, R. J., Larsen, M., She, C. Y., Meriwether, J. W., Hernandez, G., Jarvis, M. J., Sipler, D. P., Tepley, C. A., O'Brien, M. S., Bowman, J. R., Wu, Q., Murayama, Y., Kawamura, S., Reid, I. M., and Vincent, R. A.: An empirical model of the Earth's horizontal wind fields: HWM07, J. Geophys. Res., 113, A12304, https://doi.org/10.1029/2008JA013668, 2008.
Dunlop, M. W., Balogh, A., Glassmeier, K. H., and Robert, P.: Four-point Cluster application of magnetic field analysis tools: The Curlometer, J. Geophys. Res., 107, 1384–1397, 2002.
Earle, G. D., Klenzing, J. H., Roddy, P. A., Macaulay, W. A., Perdue, M. D., and Patrick, E. L. : A new satellite-borne neutral wind instrument for thermospheric diagnostics, Rev. Sci. Instrum., 78, 114501, https://doi.org/10.1063/1.2813343, 2007.
Earle, G. D., Davidson, R. L., Heelis, R. A., Coley, W. R., Weimer, D. R., Makela, J. J., Fisher, D. J., Gerrard, A. J., and Meriwether, J.: Low latitude thermospheric responses to magnetic storms, J. Geophys. Res.-Space, 118, 3866–3876, https://doi.org/10.1002/jgra.50212 2013.
Emery, B. A., Roble, R. G., Ridley, E. C., Killeen, T. L., Rees, M. H., Winningham, J. D., Caringan, G. R., Hays, P. B., Heelis, R. A., Hanson, W. B., Spencer, N. W., Brace, L. H., and Sugiura, M.: Thermospheric and ionospheric structure of the southern hemisphere polar cap on October 21, 1981, as determined from Dynamics Explorer 2 satellite data, J. Geophys. Res., 90, 6553–6566, 1985.
Emmert, J. T.: Thermospheric mass density: A review, Adv. Space Res., 56, 773–824, https://doi.org/10.1016/j.asr.2015.05.038, 2015.
Ergun, R. E., Tucker, S., Westfall, J., Goodrich, K. A., Malaspina, D. M., Summers, D., Wallace, J., Karlsson, M., Mack, J., Brennan, N., Pyke, B., Withnell, P., Torbert, R., Macri, J., Rau, D., Dors, I., Needell, J., Lindqvist, P.-A., Olsson, G., and Cully, C. M.: The Axial Double Probe and Fields Signal Processing for the MMS Mission, Space Sci. Rev., 199, 167–188, https://doi.org/10.1007/s11214-014-0115-x, 2016.
Fang H. and Cheng, C.: Retarding Potential Analyzer (RPA) for sounding rocket, in: An Introduction to Space Instrumentation, edited by: Oyama, K. I. and Cheng, C. Z., 139–153, 2013.
Fang, X., Randall, C. E., Lummerzheim, D., Wang, W., Lu, G., Solomon, S. C., and Frahm, R. A.: Parameterization of monoenergetic electron impact ionization, Geophys. Res. Lett., 37, L22106, https://doi.org/10.1029/2010GL045406, 2010.
Fedrizzi, M., Fuller-Rowell, T. J., and Codrescu, M. V.: Global Joule heating index derived from thermospheric density physics-based modeling and observations, Space Weather, 10, S03001, https://doi.org/10.1029/2011SW000724, 2012.
Fish, C., Swenson, C. M., Crowley, G., Barjatya, A., Neilsen, T., Gunther, J., Azeem, I., Pilinski, M., Wilder, R., Allen, D., Anderson, M., Bingham, B., Bradford, K., Burr, S., Burt, R., Byers, B., Cook, J., Davis, K., Frazier, C., Grover, S., Hansen, G., Jensen, S., LeBaron, R., Martineau, J., Miller, J., Nelsen, J., Nelson, W., Patterson, P., Stromberg, E., Tran, J., Wassom, S., Weston, V., Whiteley, M., Young, Q., Petersen, J., Schaire, S., Davis, C. R., Bokai, M., Fullmer, R., Baktur, R., Sojka, J., and Cousins, M.: Design, Development, Implementation, and On-orbit Performance of the Dynamic Ionosphere CubeSat Experiment Mission, Springer, Space Sci. Rev., 181, 61–120, https://doi.org/10.1007/s11214-014-0034-x, 2014.
Fok, M. C., Moore, T. E., Wilson, G. R., Perez, J. D., Zhang, X. X., C:Son Brandt, P., Mitchell, D. G., Roelof, E. C., Jahn, J. M., Pollock, C. J., and Wolf, R. A.: Global ENA IMAGE Simulations, in: Magnetospheric Imaging – The Image Prime Mission, edited by: Burch, J. L., Springer, Dordrecht, 2003.
Foster, J. C., St.-Maurice, J.-P., and Abreu, V. J.: Joule heating at high latitudes, J. Geophys. Res., 88, 4885–4896, 1983.
Fratter, I., Léger, J.-M., Bertrand, F., Jager, T., Hulot, G., Brocco, L., and Vigneron, P.: Swarm Absolute Scalar Magnetometers first in-orbit results Acta Astronautica, 121, 76–87, https://doi.org/10.1016/j.actaastro.2015.12.025, 2016.
Ganushkina, N. Y., Liemohn, M. W., Dubyagin, S., Daglis, I. A., Dandouras, I., De Zeeuw, D. L., Ebihara, Y., Ilie, R., Katus, R., Kubyshkina, M., Milan, S. E., Ohtani, S., Ostgaard, N., Reistad, J. P., Tenfjord, P., Toffoletto, F., Zaharia, S., and Amariutei, O.: Defining and resolving current systems in geospace, Ann. Geophys., 33, 1369–1402, https://doi.org/10.5194/angeo-33-1369-2015, 2015.
Gary, J. B., Heelis, R. A., Hanson, W. B., and Slavin, J. A.: Field aligned Poynting flux observations in the high latitude ionosphere, J. Geophys. Res., 99, 11417–11427, 1994.
Gordiets, B. F., Kulikov, Y. N., Markov, M. N., and Marov, M. Y.: Numerical modeling of the thermospheric heat budget, J. Geophys. Res., 87, 4504–4514, https://doi.org/10.1029/JA087iA06p04504, 1982.
Hanson, W., Heelis, R., Power, R., Lippincott, C., Zuccaro, D., Holt, B., Harmon, L., and Sanatani, S.: The retarding potential analyzer for dynamics explorer-b, Space Sci. Instrum., 5, 503–510, 1981.
Hanson, W. B., Ponzi, U., Arduini, C., and DiRuscio, M.: A satellite anemometer, J. Astro. Sci., 40, 429 pp., 1992.
Hatch, W. S.: Plasma velocity vector instruments for small satellites, Master's thesis, Utah State University, Logan, UT, 2016.
Hedin, A. E.: Extension of the MSIS Thermospheric Model into the middle and lower atmosphere, J. Geophys. Res., 96, 1159–1172, https://doi.org/10.1029/90JA02125, 1991.
Heise, S., Jakowski, N., Wehrenpfennig, A., Reigber, C., and Lühr, H.: Sounding of the topside ionosphere/plasmasphere based on GPS measurements from CHAMP: Initial results, Geophys. Res. Lett., 29, 44-1–44-4, 2002.
Hernandez, S., Lopez, R. E., and Wiltberger, M.: Ionospheric joule heating during magnetic storms: MHD simulations, Adv. Space Res., 36, 1845–1848, https://doi.org/10.1016/j.asr.2005.05.132, 2005.
Hoang, H, Røed, K., Bekkeng, T., Moen, J., Clausen, L., Trondsen, E., Lybekk, B., Strøm, H., Bang-Hauge, D., Pedersen, A., Nokes, C., Cupido, C., Mann, I., Ariel, M., Portnoy, D., and Sagi, E.: The Multi-needle Langmuir Probe Instrument for QB50 Mission: Case Studies of Ex-Alta 1 and Hoopoe Satellites, Space Sci. Rev., 215, 21, https://doi.org/10.1007/s11214-019-0586-x, 2019.
Janhunen, P., Palmroth, M., Laitinen, T., Honkonen, I., Juusola, L., Facskó, G., and Pulkkinen, T. I.: The GUMICS-4 global MHD magnetosphere–ionosphere coupling simulation, J. Atmos. Sol.-Terr. Phys., 80, 48–59, 2012.
Jones, M., Jr., Forbes, J. M., and Hagan, M. E.: Tidal-induced net transport effects on the oxygen distribution in the thermosphere, Geophys. Res. Lett., 41, 5272–5279, https://doi.org/10.1002/2014GL060698, 2014.
Juusola, L., Amm, O., Kauristie, K., and Viljanen, A.: A model for estimating the relation between the Hall to Pedersen conductance ratio and ground magnetic data derived from CHAMP satellite statistics, Ann. Geophys., 25, 721–736, https://doi.org/10.5194/angeo-25-721-2007, 2007.
Kelley, M.: The Earth's Ionosphere: Plasma Physics and Electrodynamics, Academic Press, 38–46, 2009.
Kestilä, A., Tikka, T., Peitso, P., Rantanen, J., Näsilä, A., Nordling, K., Saari, H., Vainio, R., Janhunen, P., Praks, J., and Hallikainen, M.: Aalto-1 nanosatellite – technical description and mission objectives, Geosci. Instrum. Method. Data Syst., 2, 121–130, https://doi.org/10.5194/gi-2-121-2013, 2013.
Kirkwood, S., Opgenoorth, H., and Murphree, J. S.: Ionospheric conductivities, electric fields and currents associated with auroral substorms measured by the EISCAT radar, Planet. Space Sci., 36, 1359–1380, https://doi.org/10.1016/0032-0633(88)90005-0, 1988.
Kivelson, M. G. and Russell, C. T.: Introduction to Space Physics, Cambridge atmospheric and space science series, Cambridge University Press, 1995.
Klenzing, J., Davidson, R., Earle, G., Halford, A., Jones, S., Martinis, C., Paschalidis, N., Santos, L., and Pfaff, R.: PetitSat – a 6U CubeSat to examine the link between MSTIDs and ionospheric plasma density enhancements, 42nd COSPAR Scientific Assembly, Held 14-22 July 2018, in: Pasadena, California, USA, Abstract id. C2.4-16-18., Pub Date: July 2018, 2018.
Klobuchar, J. A.: Ionospheric effects on GPS, in: Global Positioning System: Theory and Application, Vol. 1, edited by: Parkinson, B. W. and Spilker, J. J., American Institute of Aeronautics and Astronautics INC, Washington, 485–515, 1996.
Knipp, D. J., Welliver, T., McHarg, M. G., Chun, F. K., Tobiska, W. K., and Evans, D.: Climatology of extreme upper atmospheric heating events, Adv. Space Res., 36, 2506–2510, https://doi.org/10.1016/j.asr.2004.02.019, 2005.
Knudsen, D. J., Burchill, J. K., Berg, K., Cameron, T., Enno, G. A., Marcellus, C. G., King, E. P., Wevers, I., and King, R. A.: A low-energy charged particle distribution imager with a compact sensor for space applications, Rev. Sci. Instrum., 74, 202–211, https://doi.org/10.1063/1.1525869, 2003.
Knudsen, D. J., Bock, B. J. J., Bounds, S. R., Burchill, J. K., Clemmons, J. H., Curtis, J. D., Eriksson, A. I., Koepke, M. E., Pfaff, R. F., Wallis, D. D., and Whaley, N.: Lower-hybrid cavity density depletions as a result of transverse ion acceleration localized on the gyroradius scale, J. Geophys. Res., 109, A04212, https://doi.org/10.1029/2003JA010089, 2004.
Koskinen, H. E. J. and Tanskanen, E.: Magnetospheric energy budget and the epsilon parameter, J. Geophys. Res., 107, 1415, https://doi.org/10.1029/2002JA009283, 2002.
Laštovička, J.: Trends in the upper atmosphere and ionosphere: Recent progress, J. Geophys. Res.-Space, 118, 3924–3935, https://doi.org/10.1002/jgra.50341, 2013.
Laundal, K. M., Finlay, C. C., and Olsen, N.: Sunlight effects on the 3D polar current system determined from low Earth orbit measurements, Earth Planet. Space, 68, 1–19, https://doi.org/10.1186/s40623-016-0518-x, 2016.
Lean, J.: Calculations of Solar Irradiance: monthly means from 1882 to 2008, annual means from 1610 to 2008, available at: http://solarisheppa.geomar.de/solarisheppa/ (last access: 11 April, 2020), 2009.
Lefeuvre, F., Blanc, E., Pinçon, J.-L., Roussel-Dupre, R., Lawrence, D., Sauvaud, J.-A., Rauch, J.-L., Feraudy, H., and Lagoutte, D.: TARANIS-A satellite project dedicated to the physics of TLEs and TGFs, Space Sci. Rev., 137, 301–315, https://doi.org/10.1007/s11214-008-9414-4, 2008.
Léger, J.-M., Jager, T., Bertrand, F., Hulot, G., Brocco, L., Vigneron, P., Lalanne, X., and Fratter, I.: In-flight performance of the Absolute Scalar Magnetometer vector mode on board the Swarm satellites, Earth Planet. Space, 67, 1–12, https://doi.org/10.1186/s40623-015-0231-1, 2015.
Li, X., Schiller, Q., Blum, L., Califf, S., Zhao, H., Tu, W., Turner, D. L., Gerhardt, D., Palo, S., Kanekal, S., Baker, D. N., Fennell, J., Blake, J. B., Looper, M., Reeves, G. D., and Spence, H.: First results from CSSWE CubeSat: Characteristics of relativistic electrons in the near-Earth environment during the October 2012 magnetic storms, J. Geophys. Res.-Space, 118, 6489–6499, https://doi.org/10.1002/2013JA019342, 2013.
Lin, Z. W., Chao, C. K., Liu, J. Y., Huang, C. M., Chu, Y. H., Su, C. L., Mao, Y. C., and Chang, Y. S.: Advanced Ionospheric Probe scientific mission onboard FORMOSAT-5 satellite, Terr. Atmos. Ocean. Sci., 28, 99–110, https://doi.org/10.3319/TAO.2016.09.14.01(EOF5), 2017.
Lin, Y. C. and Chu, Y. H.: Model simulations of ion and electron density profiles in ionospheric E and F regions, J. Geophys. Res.-Space, 122, 2505–2529, https://doi.org/10.1002/2016JA022855, 2017.
Lopez, R. E., Wiltberger, M., and Lyon, J. G.: Coupling between the solar wind and the magnetosphere during strong driving: MHD Simulations, IEEE Trans. Plasma Sci., 32, 1439–1442, https://doi.org/10.1109/TPS.2004.834037, 2004.
MacManus D. H., Rodger, C. J., Dalzell, M., Thomson, A. W. P., Clilverd, M. A., Petersen, T., Wolf, M. M., Thomson, N. R., and Divett, T.: Long-term geomagnetically induced current observations in New Zealand: Earth return corrections and geomagnetic field driver, Space Weather, 15, 1020–1038, https://doi.org/10.1002/2017SW001635, 2017.
Malaspina, D. M., Ergun, R. E., Bolton, M., Kien, M., Summers, D., Stevens, K., Yehle, A., Karlsson, M., Hoxie, V. C., Bale, S. D., and Goetz, K.: The Digital Fields Board for the FIELDS instrument suite on the Solar Probe Plus mission: Analog and digital signal processing, J. Geophys. Res.-Space, 121, 5088–5096, https://doi.org/10.1002/2016JA022344, 2016.
McCrea, I., Aikio, A., Alfonsi, L., Belova, E., Buchert, S., Clilverd, M., Engler, N., Gustavsson, B., Heinselman, C., Kero, J., Kosch, M., Lamy, H., Leyser, T., Ogawa, Y., Oksavik, K., Pellinen-Wannberg, A., Pitout, F., Rapp, M., Stanislawska, I., and Vierinen, J.: The science case for the EISCAT_3D radar, Prog. Earth Plane. Sc., 2, 21, https://doi.org/10.1186/s40645-015-0051-8, 2015.
Mozer, F. S.: DC and low-frequency double probe electric field measurements in space, J. Geophys. Res.-Space, 121, 10942–10953, https://doi.org/10.1002/2016JA022952, 2016.
Ogawa, Y., Motoba, T., Buchert, S. C., Häggström, I., and Nozawa, S.: Upper atmosphere cooling over the past 33 years, Geophys. Res. Lett., 41, 5629–5635, https://doi.org/10.1002/2014GL060591, 2014.
O'Hanlon, J. F.: A User's Guide to Vacuum Technology, 2nd Edn., John Wiley, New York, 1989.
Olsson, A., Janhunen, P., Karlsson, T., Ivchenko, N., and Blomberg, L. G.: Statistics of Joule heating in the auroral zone and polar cap using Astrid-2 satellite Poynting flux, Ann. Geophys., 22, 4133–4142, https://doi.org/10.5194/angeo-22-4133-2004, 2004.
Palmroth, M., Janhunen, P., Pulkkinen, T. I., and Koskinen, H. E. J.: Ionospheric energy input as a function of solar wind parameters: global MHD simulation results, Ann. Geophys., 22, 549–566, https://doi.org/10.5194/angeo-22-549-2004, 2004.
Palmroth, M., Janhunen, P., Pulkkinen, T. I., Aksnes, A., Lu, G., Østgaard, N., Watermann, J., Reeves, G. D., and Germany, G. A.: Assessment of ionospheric Joule heating by GUMICS-4 MHD simulation, AMIE, and satellite-based statistics: towards a synthesis, Ann. Geophys., 23, 2051–2068, https://doi.org/10.5194/angeo-23-2051-2005, 2005.
Palmroth, M., Janhunen, P., Germany, G., Lummerzheim, D., Liou, K., Baker, D. N., Barth, C., Weatherwax, A. T., and Watermann, J.: Precipitation and total power consumption in the ionosphere: Global MHD simulation results compared with Polar and SNOE observations, Ann. Geophys., 24, 861–872, https://doi.org/10.5194/angeo-24-861-2006, 2006.
Park, J., Lühr, H., Kervalishvili, G., Rauberg, J., Stolle, C., Kwak, Y. S., and Lee, W. K.: Morphology of high-latitude 10 plasma density perturbations as deduced from the total electron content measurements onboard the Swarm constellation, J. Geophys. Res.-Space, 122, 1338–1359, 2017.
Parrot, M.: The micro-satellite DEMETER, J. Geodyn., 33, 535–541, https://doi.org/10.1016/S0264-3707(02)00014-5, 2002.
Paschalidis, N., Jones, S. L., Rodriguez, M., Sittler, E. C. Jr., and Chornay, D. J.: A Compact Ion Neutral Mass Spectrometer for the ExoCube Mission, 6th European CubeSat Symposium, Estavayet, Switzerland, 2014.
Picone, J. M., Hedin, A. E., Drob, D. P., and Aikin, A. C.: NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues, J. Geophys. Res.-Space, 107, 1468, https://doi.org/10.1029/2002JA009430, 2002.
Prölss, G. W.: Density Perturbations in the Upper Atmosphere Caused by the Dissipation of Solar Wind Energy, Survey. Geophys., 32, 101–195, https://doi.org/10.1007/s10712-010-9104-0, 2011.
Pulkkinen, A., Bernabeu, E., Thomson, A., Viljanen, A., Pirjola, R., Boteler, D., Eichner, J., Cilliers, P. J., Welling, D., Savani, N. P., Weigel, R. S., Love, J. J., Valch, C., Ngwira, C. M., Crowely, G., Schultz, A., Kataoka, R., Anderson, B., Fugate, D., Simpson, J. J., and MacAlester, M.: Geomagnetically induced currents: Science, engineering, and applications readiness, Space Weather, 15, 828–856, https://doi.org/10.1002/2016SW001501, 2017.
Qian, L., Laštovička, J., Roble, R. G., and Solomon, S. C.: Progress in observations and simulations of global change in the upper atmosphere, J. Geophys. Res., 116, A00H03, https://doi.org/10.1029/2010JA016317, 2011.
Randall, C. E., Harvey, V. L., Singleton, C. S., Bailey, S. M., Bernath, P. F., Codrescu, M., Nakajima, H., and Russell III, J. M.: Energetic particle precipitation effects on the Southern Hemisphere stratosphere in 1992–2005, J. Geophys. Res., 112, D08308, https://doi.org/10.1029/2006JD007696, 2007.
Rees, M. H.: Auroral ionization and excitation by incident energetic electrons, Planet. Space Sci., 11, 1209–1218, 1963.
Rich, F. J. and Hairston, M.: Large-scale convection patterns observed by DMSP, J. Geophys. Res., 99, 3827, https://doi.org/10.1029/93JA03296, 1994.
Richmond, A. D.: Assimilative mapping of ionospheric electrodynamics, Adv. Space Res., 12, 669–668, 1992.
Richmond, A. D.: Ionospheric Electrodynamics, in: Handbook of Atmospheric Electrodynamics, Vol. II, edited by: Volland, H., CRC Press, Boca Raton, Florida, 249–290, 1995.
Richmond, A. D., Ridley, E. C., and Roble, R. G.: A thermosphere/ionosphere general circulation model with coupled electrodynamics, Geophys. Res. Lett., 19, 601–604, https://doi.org/10.1029/92GL00401, 1992.
Richmond, A. D. and Maute, A.: Ionospheric electrodynamics modeling, in: Modeling the Ionosphere-Thermosphere System, edited by: Huba, J., Schunk, R., and Khazanov, G., John Wiley, Chichester, UK, 57–71, https://doi.org/10.1002/9781118704417.ch6, 2014.
Richmond, A. D. and Thayer, J. P.: Ionospheric Electrodynamics: A Tutorial, in: Magnetospheric Current Systems, edited by: Ohtani, S., Fujii, R., Hesse, M. and Lysak, R. L., 131–146, https://doi.org/10.1029/GM118p0131, 2013.
Rishbeth, H. and Roble, R. G.: Cooling of the upper atmosphere by enhanced greenhouse gases – Modelling of thermospheric and ionospheric effects, Planet. Space Sci., 40, 1011–1026, https://doi.org/10.1016/0032-0633(92)90141-A, 1992.
Ritter, P. and Lühr, H.: Search for magnetically quiet CHAMP polar passes and the characteristics of ionospheric currents during the dark season, Ann. Geophys., 24, 2997–3009, https://doi.org/10.5194/angeo-24-2997-2006, 2006.
Ritter, P., Lühr, H., and Rauberg, J.: Determining field-aligned currents with the Swarm constellation mission, Earth Planet Sp., 65, 9, https://doi.org/10.5047/eps.2013.09.006, 2013.
Rodger, C. J., Clilverd, M. A., Green, J. C., and Lam, M. M.: Use of POES SEM-2 observations to examine radiation belt dynamics and energetic electron precipitation into the atmosphere, J. Geophys. Res., 115, A04202, https://doi.org/10.1029/2008JA014023, 2010.
Rosenqvist, L., Buchert, S., Opgenoorth, H., Vaivads, A., and Lu, G.: Magnetospheric energy budget during huge geomagnetic activity using Cluster and ground-based data, J. Geophys. Res., 111, A10211, https://doi.org/10.1029/2006JA011608, 2006.
Sangalli, L., Knudsen, D. J., Larsen, M. F., Zhan, T., Pfaff, R. F., and Rowland, D.: Rocket-based measurements of ion velocity, neutral wind, and electric field in the collisional transition region of the auroral ionosphere, J. Geophys. Res. 114, A04306, https://doi.org/10.1029/2008JA013757, 2009.
Sarris, T. E., Talaat, E. R., Lappas, V. J., and Armandillo, E.: Feasibility Study for a Low-Flying Spacecraft for the Exploration of the MLTI Region, Technical Report, ESA/ESTEC, CN 20991, 51–80, 2010.
Sarris, T. E., Talaat, E. R., Palmroth, M., Kauristie, K., and Verronen, P., and Armandillo, E.: Electrodynamics Study of the Upper Atmosphere in Support to Future MLTI Missions, Technical Report, ESA/ESTEC, CN 4000104174/11/NL/AF, 2013.
Sauvaud, J.-A., Larson, D., Aoustin, C., Curtis, D., Médale, J.-L., Fedorov, A., Rouzaud, J., Luhmann, J., Moreau, T., Schröder, P., Louarn, P., Dandouras, I., and Penou, E.: The IMPACT Solar Wind Electron Analyzer (SWEA), Space Sci. Rev., 136, 227–239, https://doi.org/10.1007/s11214-007-9174-6, 2008.
Scarf, F. L., Fredricks, R. W., Gurnett, D. A., and Smith, E. J.: The ISEE-C Plasma Wave Investigation, IEEE Transaction on Geoscience Electronics, Vol. GE-16, 1978.
Schunk, R. and Nagy, A.: Ionospheres: Physics, Plasma Physics, and Chemistry (Cambridge Atmospheric and Space Science Series), Cambridge, Cambridge University Press, 254–287, https://doi.org/10.1017/CBO9780511551772, 2004.
Semeter, J. and Kamalabadi, F.: Determination of primary electron spectra from incoherent scatter radar measurements of the auroral E region, Radio Sci., 40, RS2006, https://doi.org/10.1029/2004RS003042, 2005.
Sechi, G, André, G., Andreis, D., and Saponara, M.: Magnetic Attitude Control of the GOCE Satellite.” In 6th International ESA Conference on Guidance, Navigation and Control Systems, Loutraki, Greece, 17–20 October 2005, ESA SP-606, 2006.
Semeter, J. and Kamalabadi, F.: Determination of primary electron spectra from incoherent scatter radar measurements of the auroral E region, Radio Sci., 40, RS2006, https://doi.org/10.1029/2004RS003042, 2005.
Seppälä, A., Verronen, P. T., Kyrölä, E., Hassinen, S., Backman, L., Hauchecorne, A., Bertaux, J. L., and Fussen, D.: Solar proton events of October–November 2003: Ozone depletion in the Northern hemisphere polar winter as seen by GOMOS/Envisat, Geophys. Res. Lett., 31, L19107, https://doi.org/10.1029/2004GL021042, 2004.
Seppälä, A., Randall, C. E., Clilverd, M. A., Rozanov, E., and Rodger, C. J.: Geomagnetic activity and polar surface air temperature variability, J. Geophys. Res., 114, A10312, https://doi.org/10.1029/2008JA014029, 2009.
Sinnhuber, M., Nieder, H., and Wieters, N.: Surv Geophys: Energetic Particle Precipitation and the Chemistry of the Mesosphere/Lower Thermosphere, Surv. Geophys., 33, 1281–1334, https://doi.org/10.1007/s10712-012-9201-3, 2012.
Slinker, S. P., Fedder, J. A., Emery, B. A., Baker, K. B., Lummerzheim, D., Lyon, J. G., and Rich, F. J.: Comparison of global MHD simulations with AMIE simulations for the events of 19–20 May, 1996, J. Geophys. Res., 104, 28379–28395, 1999.
Solomon, S. C.: Global modeling of thermospheric airglow in the far ultraviolet, J. Geophys. Res.-Space, 122, 7834–7848, https://doi.org/10.1002/2017JA024314, 2017.
Solomon, S. C., Qian, L., and Roble, R. G.: New 3-D simulations of climate change in the thermosphere, J. Geophys. Res.-Space, 120, 2183–2193, https://doi.org/10.1002/2014JA020886, 2015.
Stoneback, R. A., Davidson, R. L., and Heelis, R. A.: Ion drift meter calibration and photoemission correction for the C/NOFS satellite, J. Geophys. Res., 117, A08323, https://doi.org/10.1029/2012JA017636, 2012.
Stromberg, E.: DICE CubeSat Mission, 8th Annual CubeSat Developers' Workshop, CalPoly, San Luis Obispo, CA, USA, 20–22 April 2011, 2011.
Sutton, E. K., Nerem, R. S., and Forbes, J. M.: Density and Winds in the Thermosphere Deduced from Accelerometer Data, J. Spacecraft Rockets, 44, 1210–1219, https://doi.org/10.2514/1.28641, 2007.
Swenson, A. P.: The Field-Programmable Gate Array Design of the Gridded Retarding Ion Distribution Sensor, All Graduate Theses and Dissertations, 6876, available at: https://digitalcommons.usu.edu/etd/6876, 2017.
Thayer, J. P. and Semeter, J.: The convergence of magnetospheric energy flux in the polar atmosphere, J. Atmos. Sol.-Terr. Phys., 66, 807–824, 2004.
Trotignon, J. G., D'eau, P. M. E., Rauch, J. L., Le Guirriec, J., Canu, P., and Darrouzet, F.: The Whisper Relaxation Sounder Onboard Cluster: A Powerful Tool for Space Plasma Diagnosis around the Earth, Cosmic Res., 41, 345–348, 2003.
Trotignon, J. G., Michau, J. L., Lagoutte, D., Chabassiere, M., Chalumeau, G., Colin, F., Decreau, P. M., Geiswiller, J., Gille, P., Grard, R., Hachemi, T., Hamelin, M., Eriksson, A., Laakso, H., Lebreton, J. P., Mazelle, C., Randriamboarison, O., Schmidt, W., Smit, A., Telljohann, U., and Zamora, P.: RPC-MIP: The Mutual Impedance Probe of the Rosetta Plasma Consortium, Space Sci. Rev., 128, 713–728, https://doi.org/10.1007/s11214-006-9005-1, 2007.
Vasyliūnas, V. M. and Song, P.: Meaning of ionospheric Joule heating, J. Geophys. Res., 110, A02301, https://doi.org/10.1029/2004JA010615, 2005.
Virtanen, I. I., Gustavsson, B., Aikio, A. T., Kero, A., Asamura, K., and Ogawa, Y.: Electron energy spectrumand auroral power estimation from incoherent scatter radar measurements, J. Geophys. Res.-Space, 123, 6865–6887, https://doi.org/10.1029/2018JA025636, 2018.
Visentine, J.: Atomic oxygen effects measurements for Shuttle missions STS-8 and 41-G (NASA Technical Memorandum 100459), Houston, TX: NASA Lyndon B. Johnson Space Center, 1983.
Visentine, J., Leger, L., Kuminecz, J., and Spiker, I.: STS-8 atomic oxygen effects experiment, American Institute of Aeronautics and Astronautics, https://doi.org/10.2514/6.1985-415, 1985.
Visser, T, Doornbos, E. N., de Visser, C. C., Visser, P. N. A. M., and Fritsche, B.: Torque model verification for the GOCE satellite, Adv. Space Res., 62, 1114–1136, 2018.
Wang, H., Lühr, H., Ma, S. Y., Weygand, J., Skoug, R. M., and Yin, F.: Field-aligned currents observed by CHAMP during the intense 2003 geomagnetic storm events, Ann. Geophys., 24, 311–324, https://doi.org/10.5194/angeo-24-311-2006, 2006.
Wayne, R.: Chemistry of Atmosphere, Oxford University Press, 2000.
Weimer, D. R.: Improved ionospheric electrodynamic models and application to calculating Joule heating rates, J. Geophys. Res., 110, A05306, https://doi.org/10.1029/2004JA010884, 2005a.
Weimer, D. R.: Predicting surface geomagnetic variations using ionospheric electrodynamic models, J. Geophys. Res., 110, A12307, https://doi.org/10.1029/2005JA011270, 2005b.
Westerhoff, J., Earle, G., Bishop, R., Swenson, G., Vadas, S., Clemmons, J., Davidson, R., Fanelli, L., Fish, C., Garg, V., Ghosh, A., Jagannatha, B., Kroeker, E., Marquis, P., Martin, D., Noel, S., Orr, C., and Robertson, R.: LAICE CubeSat mission for gravity wave studies, Adv. Space Res., 56, 1413–1427, https://doi.org/10.1016/j.asr.2015.06.036, 2015.
Wu, Q., Killeen, T. L., Deng, W., Burns, A. G., Winningham, J. D., Spencer, N. W., Heelis, R. A., and Hanson, W. B.: Dynamics Explorer 2 satellite observations and satellite track model calculations in the cusp/cleft region, J. Geophys. Res., 101, 5329–5342, 1995.
Wygant, J. R., Bonnell, J. W., Goetz, K., Ergun, R. E., Mozer, F. S., Bale, S. D., Ludlam, M., Turin, P., Harvey, P. R., Hochmann, R., Harps, K., Dalton, G., McCauley, J., Rachelson, W., Gordon, D., Donakowski, B., Shultz, C., Smith, C., Diaz-Aguado, M., Fisher, J., Heavner, S., Berg, P., Malaspina, D. M., Boltn, M. K., Hudson, M., Strangeway, R. J., Baker, D. N., Li, X., Albert, J., Foster, J.C., Chaston, C. C., Mann, I., Donovan, E., Cully, C. M., Cattell, C. A., Krasnoselskikh, V., Kersten, K., Brennemann, A., and Tao, J. B.: The Electric Field and Waves Instruments on the Radiation Belt Storm Probes Mission, Space Sci. Rev., 179, 183–220, https://doi.org/10.1007/s11214-013-0013-7, 2013.
Xiong, C., Stolle, C., and Lühr, H.: The Swarm satellite loss of GPS signal and its relation to ionospheric plasma irregularities, Space Weather, 14, 563–577, https://doi.org/10.1002/2016SW001439, 2016.
Yuan, Z., Xiong, Y., Li, H., Huang, S., Qiao, Z., Wang, Z., Zhou, M., Wang, D., Deng, X., Raita, T., and Wang, J.: Influence of precipitating energetic ions caused by EMIC waves on the subauroral ionospheric E region during a geomagnetic storm, J. Geophys. Res.-Space, 119, 8462–8471, 2014.
Zhang, X. X., Wang, C., Chen, T., Wang, Y. L., Tan, A., Wu, T. S., Germany, G. A., and Wang, W.: Global patterns of Joule heating in the high-latitude ionosphere, J. Geophys. Res., 110, A12208, https://doi.org/10.1029/2005JA011222, 2005.
Zhou, Y.-L. and Lühr, H.: Net ionospheric currents closing field-aligned currents in the auroral region: CHAMP results, J. Geophys. Res.-Space, 122, 4436–4449, https://doi.org/10.1002/2016JA023090, 2017.
Zoennchen, J. H., Nass, U., Fahr, H. J., and Goldstein, J.: The response of the H geocorona between 3 and 8 Re to geomagnetic disturbances studied using TWINS stereo Lyman-α data, Ann. Geophys., 35, 171–179, https://doi.org/10.5194/angeo-35-171-2017, 2017.
Zurbuchen, H. T., von Steiger, R., Bartalev, S., Dong, X., Falanga, M., Fléron, R., Gregorio, A., Horbury, T. S., Klumpar, D., Küppers, M., Macdonald, M., Millan, R., Petrukovich, A., Schilling, K., Wu, J., and Yan, J.: Performing High-Quality Science on CubeSats, Space Research Today, 196, 11–30, https://doi.org/10.1016/j.srt.2016.07.011, 2016.
ignorosphere. Here, intriguing and complex processes govern the deposition and transport of energy. The aim is to quantify this energy by measuring effects caused by electrodynamic processes in this region. The concept is based on a mother satellite that carries a suite of instruments, along with smaller satellites carrying a subset of instruments that are released into the atmosphere.