Intercomparison of cosmic-ray neutron sensors and water balance monitoring in an urban environment

Sensor-to-sensor variability is a source of error common to all geoscientific instruments that needs to be assessed before comparative and applied research can be performed with multiple sensors. Consistency among sensor systems is especially critical when subtle features of the surrounding terrain are to be identified. Cosmic-ray neutron sensors (CRNSs) are a recent technology used to monitor hectometre-scale environmental water storages, for which a rigorous comparison study of numerous co-located sensors has not yet been performed. In this work, nine stationary CRNS probes of type “CRS1000” were installed in relative proximity on a grass patch surrounded by trees, buildings, and sealed areas. While the dynamics of the neutron count rates were found to be similar, offsets of a few percent from the absolute average neutron count rates were found. Technical adjustments of the individual detection parameters brought all instruments into good agreement. Furthermore, we found a critical integration time of 6 h above which all sensors showed consistent dynamics in the data and their RMSE fell below 1 % of gravimetric water content. The residual differences between the nine signals indicated local effects of the complex urban terrain on the scale of several metres. Mobile CRNS measurements and spatial simulations with the URANOS neutron transport code in the surrounding area (25 ha) have revealed substantial sub-footprint heterogeneity to which CRNS detectors are sensitive despite their large averaging volume. The sealed and constantly dry structures in the footprint furthermore damped the dynamics of the CRNS-derived soil moisture. We developed strategies to correct for the sealed-area effect based on theoretical insights about the spatial sensitivity of the sensor. This procedure not only led to reliable soil moisture estimation during dry-out periods, it further revealed a strong signal of intercepted water that emerged over the sealed surfaces during rain events. The presented arrangement offered a unique opportunity to demonstrate the CRNS performance in complex terrain, and the results indicated great potential for further applications in urban climate research.

1 Introduction

The monitoring of water states and fluxes is important to understand processes of the hydrological cycle, to facilitate weather predictions, and to make timely decisions (Wood et al., 2011; Beven and Cloke, 2012). Soil moisture and air humidity are interlinked key quantities that can control plant water availability, groundwater recharge, air temperature, and regional weather phenomena (Seneviratne et al., 2010). In urban environments, sealed surfaces reduce water infiltration and promote high evaporation from ponded water. These effects are linked with the formation and impact of urban heat islands and can be a major threat for society (Arnfield, 2003; Starke et al., 2010; UN, 2015).

Conventional measurement methods for soil and evaporation water operate on a point scale and are not representative of complex areas (Famiglietti et al., 2008; Schelle et al., 2013), while remote-sensing products are often limited to low resolution and shallow penetration depth (Nouri et al., 2013; Fang and Lakshmi, 2014). Up to now, few methods have been available to assess the components of the hydrological cycle non-invasively and on relevant scales (Robinson et al., 2008).

The method of cosmic-ray neutron sensing (CRNS) combines the geoscientific research fields of cosmic-ray neutron detection and environmental hydrology (Desilets et al., 2010; Zreda et al., 2012). The instrument is an epithermal neutron detector that measures the natural cosmic-ray-induced radiation 1–2 m above the ground and is highly sensitive to the abundance of hydrogen atoms in the surrounding area. As neutrons can penetrate the soil up to depths of approximately 80 cm and are then able to travel several hundreds of metres in air, the unique feature of the technology is the large averaging volume (Köhli et al., 2015). The CRNS research field aims to fill the gap between point-scale and large-scale measurements by using the sensor in a stationary and mobile mode. The main advantages of the method are its capabilities to capture different components of the water cycle in air, soil, and vegetation non-invasively (e.g. Baroni and Oswald, 2015) and to provide a representative spatial average of the environmental water content. Therefore, the method is a promising candidate to support hydrogeophysical and climate research in complex terrain (e.g. urban environments).

Consistency among the neutron signals is an important prerequisite towards joint usage of multiple sensors for scientific applications. Many studies relied on the consistent performance of a set of CRNS probes for monitoring (Rivera Villarreyes et al., 2011; Dong et al., 2014; Franz et al., 2015; Evans et al., 2016), modelling (Rosolem et al., 2014; Baatz et al., 2017; Andreasen et al., 2016), or remote-sensing validation purposes (Holgate et al., 2016; Montzka et al., 2017). Intercomparison studies are a preferable way to find sensor-to-sensor inconsistencies. Geoscientific instruments such as point-scale soil moisture probes and remote-sensing instruments typically undergo intercomparison (Walker et al., 2004; Kögler et al., 2013; Su et al., 2013), and the CRNS technology should not be an exception.

The main application of intercomparison studies is intercalibration, the determination of efficiency (or scaling) factors for individual devices (see e.g. Baatz et al., 2015; Franz et al., 2015). Neutron detector signals often exhibit systematic biases due to limitations in manufacturing and small differences in geometry and materials utilized. For example, Chiba et al. (1975) and Oh et al. (2013) revealed clear discrepancies between high-energy neutron monitors which were related to device-specific configurations. Intercalibration may be employed to normalize such differences from unit to unit and also to account for any residual instrumental configuration inconsistencies (Bachelet et al., 1965; Krüger et al., 2008).

When it comes to data analysis and interpretation, spatial heterogeneity could have a biasing effect on neutron detectors. Despite the large footprint, the sensor is not equally sensitive to every part. Its radial sensitivity decreases non-linearly with distance, showing pronounced sensitivity to the nearest few metres around the probe (Köhli et al., 2015). This might become a particular issue for co-located sensors during an intercomparison study and for the reliability of soil moisture estimations in complex terrain (Franz et al., 2013; Schrön et al., 2017a). Nonetheless, researchers have challenged the task to interpret CRNS data in complex environments (Bogena et al., 2013; Franz et al., 2016; Schattan et al., 2017; Schrön et al., 2017b), but open questions remain of how and to what degree spatial heterogeneity should be accounted for.

The CRNS measurements come with an intrinsic statistical uncertainty which is higher for lower count rates and decreases with longer integration time. Among others, Evans et al. (2016) and Hawdon et al. (2014) reported issues with low hourly count rates in wet regions and at low altitude. Bogena et al. (2013) found that the error in volumetric soil moisture estimates can be 10–20 % for hourly CRNS data in a forested environment. This statistical noise might become a problem for the reliability and consistency of CRNS measurements.

The main objective of this paper is to advance the generation of reliable CRNS products. To achieve this, we aim to explore the potential sensor-to-sensor variability of cosmic-ray neutron sensors in a systematic way and to provide solutions to improve the consistency of neutron measurements. With regards to the potential sources of variability in the neutron signal, we can formulate the following hypotheses:

• A.

  The integrated neutron measurements may be sensitive to sensor location within a few metres.

• B.

  Device-specific differences may cause systematic variations between the sensors.

• C.

  Statistical noise contributes to the count rate variability and determines the degree of comparability between sensors.

The hypotheses are tested using nine co-located CRNS probes within a maximum distance of 15 m in an urban environment. Hypothesis A was addressed by investigating the effect of sensor permutation on the neutron counts. Hypothesis B was tested by changing detection parameters of the sensors. Correlation and consistency tests of the sensor ensemble were performed with regards to temporal aggregation to address hypothesis C.

To further understand the influence of sensor location, simulations and mobile measurements were consulted to reveal the spatial heterogeneity of neutrons within the footprint. We finally evaluated the sensor performance against independent soil moisture observations, using a new approach to correct the neutron signal for the unwanted contribution of sealed areas in the footprint.

2 Methods and instrumentation

2.1 Cosmic-ray neutron sensors

Neutrons in the energy range of 10 to 10⁴ eV are highly sensitive to hydrogen, which turns neutron detectors to highly efficient proxies for changes of environmental water content. Zreda et al. (2012) presented the established method of cosmic-ray neutron sensing as a non-invasive and promising tool for hydrology applications. Köhli et al. (2015) provided more details of the underlying physics, the lateral footprint of several tens of hectares, and the sample depth of up to 80 cm (see also Franz et al., 2012; Desilets and Zreda, 2013).

Neutron sensors of type “CRS1000” (Hydroinnova LLC, US) have been the standard in CRNS research and are commercially available in several configurations. The main components and configurations have been described by Zreda et al. (2012) and are summarized in Fig. 1a (see also the manufacturer's web page: http://hydroinnova.com/ps_soil.html\#stationary). Each system comprises a bare and a moderated neutron detector, two advanced neutron pulse detecting modules (NPM), and a data logger with integrated telemetry. The mentioned components are housed in a sealed metal enclosure. The logger retrieves neutron counts and diagnostic pulse height information periodically from each NPM, which generate the high voltage required by the detector tubes. The data logger also samples from barometric pressure sensors and, in this work, from an external temperature and air humidity sensor (Campbell CS215, Campbell Scientific Inc., Logan, Utah, US). The data logger has further been configured to record signals from a tipping bucket rain gauge.

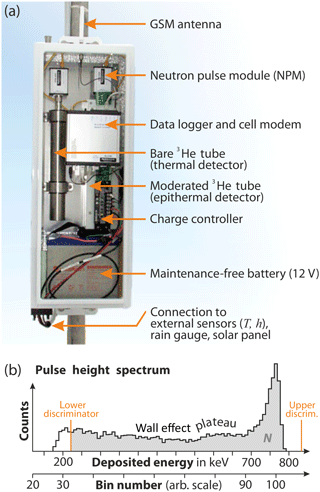
Figure 1 (a) Inside view of the cosmic-ray neutron sensor (CRNS) of type “CRS1000”. The moderated tube (surrounded by a white polyethylene block) mainly detects epithermal neutrons and is thus sensitive to water in the environment. (b) A typical, measured pulse height spectrum (PHS) shows the deposited energy in the gas tube. Upper and lower discriminators (orange) delimit the region (grey) in which events are interpreted as neutron counts N. Illustrated discriminator positions are examples. The internal representation of released energy as bin numbers is a specific feature of the sensor.

2.2 The mobile CRNS rover

The cosmic-ray neutron rover is technically similar to the stationary CRNS probes. The main differences are the added GPS functionality and much larger counting gas tubes. The larger size of the detector increases the probability to capture a neutron and consequently leads to higher count rates by factors of ≈ 11 compared to the stationary probes. This also allows for shorter integration periods of 1 min. The length of the track passed in that minute determines the spatial resolution of the measurement. Previous studies used the rover mainly to survey soil moisture on the regional scale (McJannet et al., 2014; Dong et al., 2014; Chrisman and Zreda, 2013; Wolf et al., 2016), in agricultural fields (Franz et al., 2015; Schrön et al., 2017b), and also in urban areas (Chrisman and Zreda, 2013). In this study we aim to determine the spatial distribution of neutrons within parts of the stationary CRNS footprint.

2.3 Neutron detection

A polyethylene shielded detector is employed to provide a moderated detector channel. The shielding material is designed to reduce the number of incoming thermal neutrons and to slow incoming epithermal neutrons down to thermal (i.e. detectable) energies. An additional bare detector in the CRNS probe directly records incoming thermal neutrons, while it is less sensitive to epithermal energies (Andreasen et al., 2016; Köhli et al., 2018).

2.3.1 Interactions with the detector gas

Only thermal neutrons can be efficiently detected with state-of-the-art proportional detectors employing gases enriched in ³He (Persons and Aloise, 2011; Krane and Halliday, 1988). When a thermal neutron collides with an atomic nucleus of the detector gas, a neutron absorption reaction can occur, resulting in emission of charged particles, which in turn produce ionization. Electrons are attracted to the anode, a central wire at a potential of ≈ 1000 V. Due to the steep gradient of the electrical potential towards the wire, the electrons are accelerated and collide with additional gas molecules, producing further ionization. A sensitive NPM, consisting of hybrid analogue–digital electronics, amplifies, shapes, and filters each charge pulse from the tube. The NPM further measures the pulse height and records it as a neutron count if it is a valid event. The pulse is further accumulated in a pulse height spectrum (PHS).

2.3.2 Pulse height spectrum recordings

As the energy of the reaction products in the gas is well known, a characteristic electronic pulse can be expected and translates to a prominent peak in a so-called pulse height spectrum (see Fig. 1b). However, sometimes the elements of the reaction product reach the wall of the tube before completely depositing their energy into the proportional gas. The so-called “wall effect” is then visible in the PHS as a distribution of pulses of lower pulse height than the peak. As such, the typical shape of the PHS is independent of the absorbed neutron energy. It is rather a function of the reaction kinematics and detector-specific details, including the geometry (Crane and Baker, 1991).

Pulse height spectra are autonomously and periodically recorded (typically daily or every several days) by the CRNS detector system, providing valuable self-diagnostics and long-term monitoring of the system health. An irregular PHS can have multiple reasons, for example collapsing high-voltage supply, gas leakage, or impurity in the detector tube, while variations at the lower end are an indication for current noise or gamma radiation. Typical CRNS systems have stable, long-term sensitivity to neutrons and are maximally immune to environmental changes (such as temperature), electronic noise, and instrumental drift. More information about neutron detectors can be found for example in Mazed et al. (2012) and Persons and Aloise (2011).

2.3.3 The lower discriminator

The detector recognizes a neutron capture event if the released electronic pulse lies between the lower discriminator at the lower end and the upper discriminator at the upper end of the PHS (beyond the prominent peak). The lower discriminator is an important detection parameter that is often set up on the “wall-effect shelf” (the flat plateau in Fig. 1b), slightly to the right of the lower shelf edge (bins 30–35). This ensures maximum immunity to lower amplitude electronic noise which could otherwise be counted as neutron events. In addition, a high discriminator excludes signals from gamma pileups which could otherwise produce spurious counts when in the presence of significant gamma radiation. However, the discriminator position above the shelf results in some loss of the theoretical maximum sensitivity of the neutron detector and can cause some variation in sensitivity if the location of the lower discriminator relative to the peak location is not set consistently across multiple sensors.

Improvements in the NPM electronics since 2013 have increased the stability of the electronic gain and the high voltage supply, as well as lowered the electronic noise floor. Therefore it is reasonable to use the whole pulse height spectrum for the neutron counter by setting the lower discriminator below the wall effect shelf (around bin 24). One of the benefits is in maximally counting all neutrons (i.e. essentially counting very close to 100 % of all neutron capture events). In addition, in such a configuration, small changes in NPM electronic gain or internal high voltage will have the most minimal effect on the count rate.

2.4 Data processing and analysis

2.4.1 From neutrons to soil moisture

The measured intensity of albedo neutrons depends not only on the water content in the environment but also on the intensity of incoming cosmic-ray neutrons. This radiation component changes with changing atmospheric conditions and also with incoming galactic cosmic rays (Zreda et al., 2012). For this reason, CRNSs are typically equipped with sensors for air pressure p, air temperature T, and relative humidity h_rel. Their compound average, 〈⋅〉, was utilized to correct individual neutron count rates N_raw using standard procedures:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\displaystyle }N=N_{\text{raw}}& {\displaystyle }\cdot (\mathrm{1}+\mathit{\alpha }(〈h〉-h_{\text{ref}}\left)\right)\\ {\displaystyle }& {\displaystyle }\cdot \exp \left(\mathit{\beta }\right(〈p〉-p_{\text{ref}}\left)\right)\\ {\displaystyle }& {\displaystyle }\cdot (\mathrm{1}+\mathit{\gamma }(I_{\text{ref}}/I-\mathrm{1}\left)\right),\end{array}\end{array}$$

where h(h_rel,T) is the absolute humidity, I is the incoming radiation (here the average signal from neutron monitors Jungfraujoch and Kiel), h_ref=0 g m⁻³, p_ref=1013.25 mbar, I_ref=150 cps, α=0.0054, β=0.0076, and γ=1 (for details see Zreda et al., 2012; Rosolem et al., 2013; Hawdon et al., 2014; Schrön et al., 2015). The accepted approach to convert neutron count rates to (soil) water equivalent θ uses the following relation:

$$\begin{array}{}\text{(2)}& \mathit{\theta }\left(N\right)\cdot {\mathit{\varrho }}_{\text{bulk}}={\displaystyle \frac{\mathrm{0.0808}}{N/N_{\mathrm{0}}-\mathrm{0.372}}}-\mathrm{0.115}-{\mathit{\theta }}_{\text{offset}},\end{array}$$

where ϱ_bulk (in g cm⁻³) is the soil bulk density, θ_offset (in g∕g) is the gravimetric water equivalent of additional hydrogen pools (e.g. lattice water, soil organic carbon), and N₀ (in counts per hour, cph) is a free calibration parameter (for details see Desilets et al., 2010; Bogena et al., 2013). The latter can be calibrated using the count rate N and independent measurements of the average water content 〈θ〉 in the footprint. According to Schrön et al. (2017a) the CRNS probe does not measure a simple, equally weighted average of the surrounding water content due to the non-linearity of its radial sensitivity function, W_r(h,θ). Therefore, different parts of the footprint area contribute differently to the average signal depending on their distance r from the sensor. This knowledge can be used to quantify the contribution of individual areas that are of specific interest.

2.4.2 Counting statistics

Nine CRNS probes were employed for the intercomparison study and each member of the CRNS ensemble acts as an individual monitoring system. The co-location of these sensors, however, offers a unique opportunity to combine their signals, which leads to high total count rates and thus lower statistical noise. The average count rate 〈N〉 and its propagated uncertainty σ of each ith sensor are given as

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\displaystyle }〈N〉& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{9}}}\sum N_i,\\ {\displaystyle }\mathit{\sigma }\left(〈N〉\right)& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{9}}}\sqrt{\sum \mathit{\sigma }(N_i{)}^{\mathrm{2}}},\end{array}\end{array}$$

where $\mathit{\sigma }\left(N\right)=\sqrt{N}$ is given as the standard deviation of average counts N using Gaussian statistics, and 9 is the number of individual sensors used in this study. Under the assumption that $N_i\approx N_j\forall i,j\in (\mathrm{1},\mathrm{\dots },\mathrm{9})$, their corresponding uncertainty will be similar as well:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\displaystyle }\mathit{\sigma }\left(N_i\right)& {\displaystyle }\approx 〈\mathit{\sigma }\left(N_i\right)〉\forall i,\\ {\displaystyle }\Rightarrow \mathit{\sigma }\left(〈N〉\right)& {\displaystyle }\approx {\displaystyle \frac{\mathrm{1}}{\mathrm{9}}}\sqrt{\mathrm{9}\cdot {〈\mathit{\sigma }\left(N_i\right)〉}^{\mathrm{2}}}\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}〈\mathit{\sigma }\left(N_i\right)〉\approx {\displaystyle \frac{\mathrm{1}}{\mathrm{3}}}\sqrt{〈N〉}.\end{array}\end{array}$$

Hence, the combination of nine sensors reduces the relative statistical error by ≈ 67 %, thereby allowing for accurate measurements of changes of the environmental water storage.

Temporal aggregation can further reduce the standard deviation. The measurement interval τ is usually set to 1 h, while the count rate N is given in units of cph. Aggregation of the time series N to longer intervals leads to the series N_a (counts per a hours), where a is an arbitrary factor following τ_a=a τ. In order to keep cph as the standard reference unit for all neutron time series, the units can be transformed back to τ (i.e. 1 h). Then the average count rate and uncertainty become

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{\displaystyle }{N}_a& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{a}}{\sum }_{\mathrm{1}}^{a}N\approx 〈N〉,\\ {\displaystyle }\mathit{\sigma }\left(N_a\right)& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{a}}\sqrt{{\sum }_{\mathrm{1}}^a\mathit{\sigma }(N{)}^{\mathrm{2}}}\approx {\displaystyle \frac{\mathrm{1}}{\sqrt{a}}}〈\mathit{\sigma }\left(N\right)〉.\end{array}\end{array}$$

As a consequence, the average statistical error of a daily aggregated time series (in units of cph) is given as $\mathit{\sigma }\left(〈N〉\right)=\sqrt{〈N〉/\mathrm{24}}$, which corresponds to 80 % less uncertainty compared to hourly resolution.

2.4.3 Performance measures

The spread of individual sensors around their average 〈N〉 can be expressed as

$$\begin{array}{}\text{(6)}& {\mathit{\sigma }}_x\left(N\right)={\left[{\displaystyle \frac{\mathrm{1}}{\mathrm{9}}}\sum _i{\left|N_i-〈N〉\right|}^x\right]}^{\mathrm{1}/x},\end{array}$$

where the parameter x determines the distance norm. Then, σ_x=1 is defined as average absolute deviation, and ${\mathit{\sigma }}_{x=\mathrm{2}}\equiv \mathit{\sigma }$ is the standard deviation.

The Pearson correlation coefficient can be defined for two time series N_A and N_B with standard deviations σ_A and σ_B:

$$\begin{array}{}\text{(7)}& \mathit{\rho }(N_{\mathrm{A}},N_{\mathrm{B}})={\displaystyle \frac{\langle (N_{\mathrm{A}}-〈N_{\mathrm{A}}〉)\cdot (N_{\mathrm{B}}-〈N_{\mathrm{B}}〉)\rangle }{{\mathit{\sigma }}_{\mathrm{A}}\cdot {\mathit{\sigma }}_{\mathrm{B}}}}.\end{array}$$

For example, ρ=0.7 depicts that N_A and N_B can explain 0.7²≈50 % of their respective variance. If those two variables, N_A and N_B, were ranked depending on the order of their magnitude, N_i↦rank(N_i), the Pearson correlation turns to the so-called Spearman rank correlation:

$$\begin{array}{}\text{(8)}& {\mathit{\rho }}_S(N_{\mathrm{A}},N_{\mathrm{B}})=\mathrm{1}-\mathrm{6}{\displaystyle \frac{{\sum }_t\left(\text{rank}\right(N_{\mathrm{A}})-\text{rank}(N_{\mathrm{B}}){)}^{\mathrm{2}}}{n(n^{\mathrm{2}}-\mathrm{1})}},\end{array}$$

where n is the total number of intervals and $t\in (\mathrm{1},\mathrm{\dots },n)$. This quantity can be used to identify events that changed the rank of specific sensors.

Table 1 Two soil profiles in the grass meadow sampled nearby the profiles of the wireless sensor network (WSN) on 14 January 2016. Samples were taken with core cutters of constant volume at three depths, oven-dried, and weighted according to standard procedures. The evaporated water content is given in units of volumetric percent.

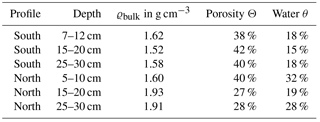
Table 2 Measurement strategy to investigate the sensor-to-sensor variability (Phase I), the influence of location (Phase II), the effects of detector parameters (Phase III), the heterogeneity of neutrons within the sensor's footprint (Survey), and the sensor's capabilities to monitor soil moisture in the complex, urban terrain.

2.5 The neutron transport simulator URANOS

The generation, interaction, and detection of neutrons can be simulated with Monte Carlo codes, which are based on physically modelled interaction processes, and state-of-the-art nuclear cross section databases. The Ultra Rapid Adaptable Neutron-Only Simulation (URANOS) has been specifically tailored to environmental neutrons relevant for CRNS research. The model was described by Köhli et al. (2015) to calculate the footprint volume and spatial sensitivity of CRNS probes. It has since been successfully applied to advance the method of cosmic-ray neutron sensing (Schrön et al., 2015, 2017a) and also to advance research in nuclear physics to simulate neutron detectors and characterize their response on the millimetre scale (Köhli et al., 2016, 2018). One of the unique features is the simulation of spatial neutron densities in an arbitrary, user-defined terrain. URANOS is very flexible and allows to input spatial bitmap information about the materials and geometries in the studied area. The software comes with a graphical user interface and is freely available (see www.ufz.de/uranos).

The urban scenario of 500 m×500 m around the CRNS probes was re-enacted using 2-D images of different layers that represent the different material compositions. More than 145 million neutrons were released equally distributed in heights of 80 to 50 m. The simulation domain in total covered a volume of 900 m×900 m and 1000 m height, where the additional padding around the area accounts for border effects. Non-sealed area was defined as grassland with an exemplary soil moisture of 30 %. Buildings were modelled as blocks of air by a 0.5 m concrete wall. Trees were modelled as blocks of organic material with 0.3 kg m⁻³ biomass stretching to heights of up to 20 m. Details of all materials used can be found in the Supplement of this paper. Simulated neutrons were counted in a detector layer 1.75 m above the surface, representing the typical position of cosmic-ray neutron sensors.

2.6 Point-scale soil moisture measurements

In order to validate and calibrate the sensors against independent soil water content, two measurement methods were consulted to quantify soil moisture profiles: volume soil samples (single measurement) and a mobile wireless ad hoc soil moisture network (WSN) (continuous). The measurements were taken in different depths at two locations near the CRNS probes. The corresponding soil parameters (Table 1) and time series data have been utilized to calibrate the neutron signal on volumetric soil moisture using Eq. (2).

WSN is a promising tool in the field of environmental science to detect and record energy and matter fluxes across Earth's compartments (Hart and Martinwz, 2006; Zerger et al., 2010; Corke et al., 2010). The WSN used in this study was developed specifically for short-term, demand-driven applications (Mollenhauer et al., 2015; Bumberger et al., 2015). The soil moisture sensors of type Truebner SMT100 used in the soil profiles directly measure electrical permittivity, ε, which is a compound quantity of the individual media (water, soil, air) and their volumetric fractions in the soil (Brovelli and Cassiani, 2008). The volumetric water content θ was deduced from ε with the CRIM formula (Roth et al., 1990), using independent measurements of porosity and soil water temperature and assuming randomly aligned microscopic soil structures. The measurement uncertainties in units of absolute volumetric percent could be related to the device (<2 %) and could vary from wet to dry conditions. They are highly dependent on prior calibration (Truebner, 2012) and may be related to inappropriate assumptions on the permittivity of quartz (<3 %) and to the heterogeneity of soil properties and composition in the meadow (<8 %). The latter uncertainty was tested by sampling soil moisture profiles at many places within the field and is taken into account when WSN is compared to CRNS observations.

2.7 Measurement Strategy

The study site is an urban area at the Helmholtz Centre for Environmental Research – UFZ in Leipzig, Germany ($\mathrm{51}{}^{\circ }{\mathrm{21}}^{\prime }{\mathrm{11}}^{\prime \prime }$ N, $\mathrm{12}{}^{\circ }{\mathrm{26}}^{\prime }{\mathrm{02}}^{\prime \prime }$ E; 116 m above sea level). The site exhibits humid climatic conditions and consists mainly of grassland patches surrounded by sealed areas such as roads and buildings (Fig. 2).

In February 2014, nine cosmic-ray neutron sensors were installed in a small grass meadow to monitor the neutron density in air. The sensors were co-located within a maximum distance of 15 m, which was assumed to be small relative to the sensor footprint. The individual count rates were logged every 15 min and were processed using the standard correction approaches described above.

Dedicated experiments were prepared (Table 2) to test the hypotheses whether a potential sensor-to-sensor variability is influenced by the location of the sensors (hypothesis A), by device-specific differences (hypothesis B), or by statistical noise (hypothesis C). In Phase I, the sensors were operated in the initial arrangement (see Fig. 2) for 3 weeks. Before entering Phase II, four sensors were swapped, while five sensors kept their position to serve as a reference. A comparison between Phase I and Phase II allows us to observe the effect of potential locational effects on the sensor response. After 4 weeks, detection parameters were adjusted to reduce the observed device-specific differences and to test their influence on the count rates when entering Phase III. In all phases, the correlation between the sensors and its dependence on temporal aggregation was investigated to test the influence of reduced statistical uncertainty.

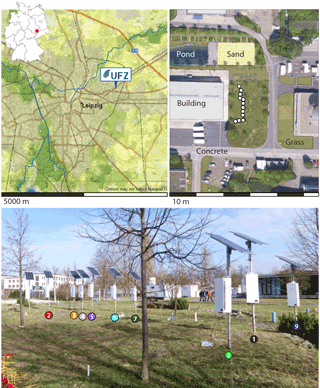
Figure 2 Location and arrangement of the nine cosmic-ray neutron sensors deployed at the small, urban meadow at UFZ Leipzig, Germany.

In order to fully understand implications of hypothesis A, i.e. the effects of location on the sensor response, we performed URANOS simulations of the site-specific neutron distribution and conducted spatial surveys in parts of the CRNS footprint area. The spatial distribution of neutrons was measured with the mobile CRNS rover detector in a car (May 2014) and on a hand wagon (July 2015). To achieve a spatial resolution in the range of a few metres, the rover was operated at walking speed. Finally, the performance of the CRNS soil moisture product in such a complex terrain was questioned. The WSN was installed in two soil profiles near the CRNS sensor arrangement in order to evaluate the capabilities of the neutron sensor to estimate water content in the urban environment.

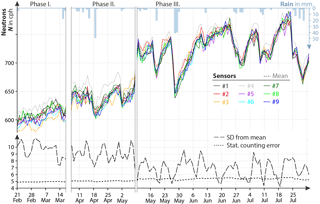
Figure 3 Time series of nine sensors covering phases I (installation), II (permutation), and III (calibration) in year 2014. By removing detector-specific effects in Phase III, the standard deviation (SD) of the sensor ensemble from their mean could be reduced down to the statistical error of σ≈5 cph.

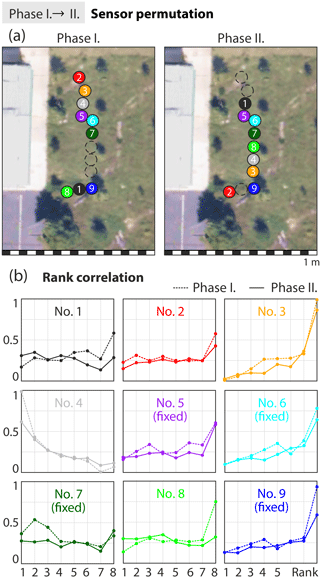
Figure 4 (a) Birds-eye view on the sensor arrangement before and after permutation of sensors 2, 3, 4, and 8. (b) Rank correlations of the nine CRNS signals before (dotted) and after (solid) permutation. Both swapped and fixed sensors showed no significant change.

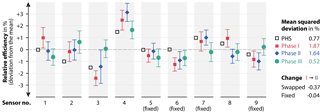
Figure 5 Relative deviation of the neutron count rates around their ensemble mean, calculated before (Phase I) and after (Phase II) the swap of sensor positions and after adjusting the detector parameters (Phase III). In addition, theoretical values before Phase III have been determined from the location of the discriminator in the pulse height spectrum (PHS, black). Error bars are based on the standard deviation of the count rate for each sensor.

3 Results and discussions

3.1 The influence of sensor location

The nine co-located sensors were operated in their initial arrangement for 3 weeks (Phase I). While all sensors showed similar trends, prominent offsets were observed between individual signals, particularly for sensors 3 and 4 (Fig. 3). The average deviation of all count rates from their ensemble mean exceeded the daily statistical error, $\mathit{\sigma }\left(N_{\mathrm{24}\mathrm{h}}\right)\approx \sqrt{\mathrm{600}/\mathrm{24}}=\mathrm{5}$, by a factor of 2.

Although the maximum distance between the sensors was only 15 m, it has been hypothesized that the individual locations could have introduced a systematic effect on the count rate due to the steep radial sensitivity curve (Köhli et al., 2015; Schrön et al., 2017a). This hypothesis A has been tested by observing the change of neutron count rates before and after the change of their position within the sensor arrangement.

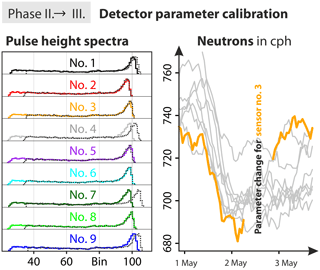
Figure 6 Adjustment of the detector parameters harmonized the pulse height spectra of the nine sensors (before: dotted black) and increased their range towards the lower left end. The impact on the count rate is shown exemplarily for sensor 3 (orange).

Before the second phase positions of a subset of sensors were swapped, while others remained fixed (Fig. 4a). In order to assess the effect on their individual measurement offsets, Spearman rank correlations were applied to the time series before and after sensor permutation (see Fig. 4b). This quantity explains the probability with which a sensor's count rate N is assigned to an ordered rank among the ensemble. The data showed that the favoured rank (or offset) of both fixed and swapped sensors was almost unaffected. In particular, the ranks of sensors 3 and 4 remained at their high or low levels, respectively.

Figure 3 further suggests that small-scale positioning has not been the main cause of the individual variability, as only subtle changes of the deviation of the sensor signals from their mean were found between phases I and II. Nevertheless, the subtle changes can be quantified in more detail by looking at the counting efficiencies of the sensors (i.e. relative deviation from their mean) in Fig. 5. The efficiency can be estimated either theoretically, by the relative positions of the lower discriminator in the PHS, or empirically, by the variability of the observed neutron counts. Figure 5 shows the theoretical relative efficiency of the nine sensors before Phase III and their empirical values in phases I, II, and III.

The results indicate that different components are contributing to the total sensor-to-sensor variability. The theoretical, detection-specific efficiency from the PHS processor accounts for only 0.77 % mean deviation, which cannot explain the high empirical values of 1.87 and 1.64 % in phases I and II, respectively. Furthermore, the fact that swapped sensors changed their mean efficiency by −0.37 %, while fixed sensors only changed by −0.04 % from Phase I to Phase II indicates that one of the additional variability components might be related to location.

All in all, a small positional effect cannot be excluded (confirming hypothesis A), but the major part of the observed sensor-to-sensor variability must have originated from other sources.

3.2 Detector-specific variability

Phase III was dedicated to the diagnosis of the count rate, which is directly related to the integral of the PHS. As explained in Sect. 2.3.2, the shape of the PHS and the parameters used to determine its integral (such as the lower discriminator) are important for the individual sensor efficiency. Thus, consistent detection parameters are a prerequisite to assure that the same fraction of neutron capture events are counted by all detectors. The inconsistent spectra in Fig. 6 (dotted black line) indicate that this requirement was not met before Phase III. Are these device-specific differences having an influence on the intercomparability of the neutron signals (hypothesis B)?

To achieve comparability of the pulse height spectra among the sensors, we set the lower discriminator consistently below the wall effect shelf (around bin 24) and adjusted the high voltage and amplifier gain parameters such that the main peaks aligned approximately to bin number 100 for the sake of visual accessibility. This procedure ensured maximum count rate for the individual sensors.

In Fig. 6 (left) the resulting change of the PHS is shown for all sensors, and the impact on the neutron count rate is demonstrated exemplarily for sensor 3. The parameter adjustments shifted the main PHS peak towards bin 100, and the reduction of the lower discriminator effectively increased the neutron count rate of the sensor. After manual adjustment of the parameters for all sensors, most of the individual offsets vanished and the standard deviation from the mean, σ(N), was reduced by 50 % down to the order of the statistical error (compare Fig. 3). Moreover, the average absolute deviation was reduced even below the statistical error $\mathit{\sigma }\left(N\right)=\sqrt{N/\mathrm{24}}$ of the daily aggregated time series (not shown). All in all, the instruments showed greater consistency in neutron counting sensitivity since the recovery of lower amplitude neutron pulse events that were previously being filtered by the lower discriminator.

In terms of relative variation (Fig. 5), the adjustment of the detector parameters at the beginning of Phase III caused the sensor efficiencies to change from 1.64 to 0.52 %. Thereby the detector-specific variability was almost removed and the sensors have since shown the best agreement to each other.

The remaining variability could be contributed to small differences in design and geometry from the manufacturer or the sensor location. The overall variability of 0.52 % is now comparable with the standard relative error of the daily mean, σ(N)∕N, which went down to 0.55 % in certain periods of this study.

3.3 Temporal resolution for consistent observations

The previous sections have shown that the CRNS probes exhibited small but measurable sensor-to-sensor variability that was related to positional effects and to the factory configuration of the neutron detector operating parameters. This section tests hypothesis C, the potential influence of statistical noise to the sensor intercomparability. The statistical variability component is related to the random nature of neutron detection. According to Sect. 2.4.2, the corresponding uncertainty can be reduced by temporal aggregation. This is expected to influence the correlation between the nine CRNS probes. While Bogena et al. (2013) calculated the uncertainties for several temporal resolutions theoretically, the present arrangement provides a unique opportunity for an experimental approach with multiple sensors.

Figure 7a shows that the ensemble-averaged correlation of the nine sensors significantly increased with increasing integration time across the three phases. The correlation coefficient was 0.12 and 0.26 for 1 h integration time and went up to 0.61 and 0.74 for 10 h in phases I and II, respectively. Since the sensor swap itself should have no effect on the correlation, the difference between Phase I and Phase II could be attributed solely to the meteorological dynamics in these periods. While rain events were almost absent during Phase I (compare Fig. 3), the corresponding neutron dynamics were mainly influenced by statistical and detector-specific variability. In Phase II, a number of rain events led to large amplitudes of neutron count dynamics and thus naturally to increased correlations.

The highest correlation was achieved in Phase III, when most of the detector-specific variability was removed (Sect. 3.2). Moreover, correlation coefficients exceeded a value of 0.90 for more than 6 h of integration time and went up to 0.97 for daily aggregation. These results demonstrate the reliability of CRNS observations for integration times of at least 6 h under humid conditions, in complex terrain, and at sea level. Even higher correlations can be expected for dry regions and homogeneous terrain at high altitude, where higher neutron count rates and less structural disturbances would lead to lower noise.

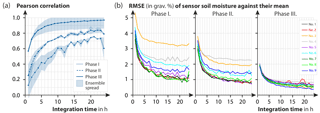
Figure 7 Influence of integration time, in hours (h), on the correlation and performance among the ensemble of nine sensors. (a) Ensemble-average Pearson correlation of the nine signals by twos for phases I, II, and III and temporal aggregation from 1 to 24 h. (b) Root mean square error of the individual soil moisture products against the soil moisture product of the ensemble mean 〈N〉. Accuracy below gravimetric water contents of 1 % can be achieved for all sensors when sensor-specific offsets were removed (Phase III) and the integration time exceeds 6 h.

The accuracy of the CRNS soil moisture product also improves for higher integration times. In Fig. 7b the effect of the temporal aggregation of neutron counts is propagated to the individual soil moisture products θ(N_i), where their root-mean-square errors (RMSEs) against the ensemble mean θ(〈N〉_i) are plotted. For all sensors, RMSEs were reduced by 50–70 % using daily aggregation, while an accuracy of 1 % gravimetric water content was achieved beyond integration times of 6 h. These findings agree quantitatively with theoretical calculations by Bogena et al. (2013) and with similar experiments using spherical neutron detectors (Figs. 8–9 in Rühm et al., 2009).

3.4 Spatial heterogeneity in the footprint area

The previous sections have confirmed that there is a measurable positional effect (hypothesis A), that device-specific variability exists (hypothesis B), and that statistical noise contributes to the measurement uncertainty (hypothesis C). Solutions have been found to overcome the latter two issues by adjusting the detector parameters or by aggregating the temporal resolution, respectively. But what can be done to better understand the influence of local structures in the CRNS footprint?

Positional effects within a few metres can occur and should be taken into account, although their effect was shown to be less important than the detector-specific variability. Several of the conducted observations supported the hypothetical influence of local effects within the complex terrain. For example, Fig. 3 shows high variability of neutron count rates in drying periods and low variability in wetting periods. This could be an effect of the dynamic size of the footprint and of the varying rates of evaporation and dewfall. According to Köhli et al. (2015), the distance which neutrons travelled before detection is smaller for wetter conditions. Thereby, distant structures could lose influence during and after rain events and thus would contribute to a harmonization of the nine sensor count rates. A second observation refers to Fig. 5, where noticeable changes of variability were observed for swapped sensors (phase transition I→II), while the behaviour of fixed sensors was almost unchanged.

The two examples indicate that local effects might have the potential to influence the sensor performance. Local sensitivity of the neutron detectors has been augured already by Köhli et al. (2015) and could be a reasonable explanation given the heterogeneous distribution of the soil, of vegetation, and of nearby structures. This section tries to further quantify the local effects in a moisture-averaging footprint of several tens of hectares, where all sensors are exposed to similar meteorological forcings.

To assess the influence of complex terrain in the urban area, neutron transport simulations were conducted with the Monte Carlo code URANOS (Sect. 2.5). The model calculated the neutron response to the structures in the footprint and simulated the neutron density that could be potentially observed with CRNS detectors in the whole area. Figure 8c shows features of low and high neutron counts on the metre scale that are related to the effects of buildings, sealed areas, the pond, iron-containing structures, and vegetation. Under these conditions it is evident that local heterogeneity in the footprint can have an effect on CRNS probes located within a distance of a few metres.

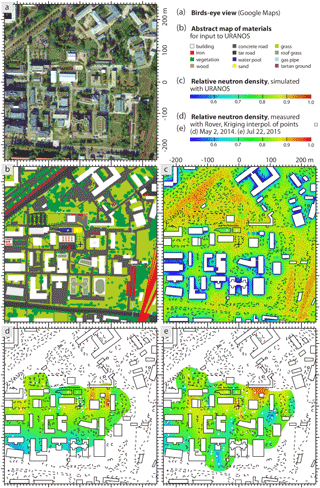
Figure 8 (a) Neutron environment of the urban CRNS test site (centred black cross). (b) Abstract model of the area using geometric shapes and colour-coded material definitions. (c) URANOS simulation of epithermal neutrons in a detector layer above the surface. (d, e) Measured neutrons with the mobile CRNS rover confirm heterogeneity of neutron patterns in the centred grass meadow as well as in the surrounding urban domain.

The URANOS model can help to assess those effects to support optimal sensor positioning or to explain unusual features in the spatial signal. The simulation results demonstrate the non-uniformity of the neutron density in the footprint. However, the simulated quantities are not expected to exactly match reality due to many modelling assumptions that have been put into the scenario (clean material composition, uniform biomass density, homogeneous soil moisture). Nevertheless, the modelled patterns can be assessed visually using measurements from a CRNS rover (Fig. 8d, e). The relative uncertainties of both the modelled and measured results are in the range of 6–9 % for ≈200 modelled neutrons per m² and ≈200 measured neutrons per minute. A direct comparison with the simulation results was not intended, as the low number of measurement points does not allow for metre-scale predictions of neutron density from the ordinary kriging interpolation. However, the collected data have been sufficient to support the theory of highly heterogeneous patterns in the urban terrain.

Both experimental and theoretical results clearly demonstrate that a significant neutron heterogeneity can occur within the CRNS footprint under conditions of complex terrain. These patterns have the potential to influence the CRNS measurements. Moreover, slight variability is evident in the small meadow (centre cross in Fig. 8), where trees and structures might influence the neutron density on a scale of a few metres. This could serve as an explanation for the minor position-related variability observed in the course of this study.

3.5 Soil moisture estimation and areal correction for sealed areas

Considering the revealed small-scale heterogeneity in the sensor footprint, as well as large sealed areas around the sensors, the important question arises whether CRNS in urban areas will be able to reliably estimate environmental water content. Therefore, we have evaluated the CRNS soil moisture product (Eq. 2) with time series data from two nearby profiles using the WSN. The locations (crosses) of each profile are shown in Fig. 9; the data were averaged and compared against the CRNS signal of sensor 7 (point).

Figure 9 shows that the CRNS soil moisture product (orange) differs significantly from the point measurements (grey dashed). Most importantly, the response to rain events appears to be much more damped in the CRNS signal. A damping effect can occur when a constant fraction of measured neutrons is independent of precipitation events.

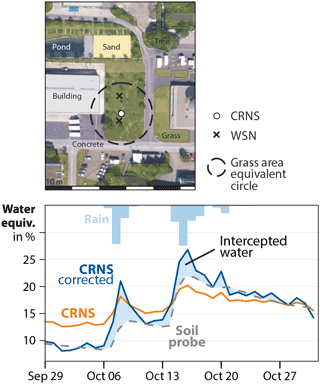
Figure 9 Top: illustration of the circular area (dashed) around the CRNS probe 7 that confines an area equivalent to the non-sealed grassland meadow. Bottom: demonstrating the area correction approach (Eq. 11). The constant contribution of neutrons from the sealed area leads to a damped signal of soil moisture dynamics measured by the CRNS (orange line). The corrected signal (blue line) shows more pronounced dynamics based only on the areal contribution of the meadow. The remaining deviation (shaded blue) from the WSN soil moisture measurements (grey dashed) probably represents intercepted water over the sealed ground during and after rain events.

The CRNS probe's footprint is much larger than the small meadow of 0.1 ha where the CRNS and the WSN probes are located. It is thus evident that the paved and sealed areas beyond the meadow could bias the integral soil moisture signal. We suspect the dry soil under the sealed surface in the footprint of having a constant and thus damping influence on the neutron signal. In the following, we aim to test the application of recent insights about the sensor's spatial sensitivity and demonstrate how this knowledge can help to understand and even correct the biasing effect of sealed areas.

Following theoretical considerations from Köhli et al. (2015) and robust evidence from Schrön et al. (2017a), the radial sensitivity function W_r(h,θ) depicts the number of detected neutrons that originated from the distance r under certain homogeneous conditions of air humidity, h, and (soil) water equivalent, θ. Its integral across all distances represents the total number of neutrons detected, N:

$$\begin{array}{}\text{(9)}& N=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{W}_r(h,\mathit{\theta })\cdot \text{d}r.\end{array}$$

A circular section of angle φ (in radiant), which is confined between radii r₁ and r₂, contributes the following fraction of neutrons n:

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{\displaystyle }n(r_{\mathrm{1}},r_{\mathrm{2}},\mathit{\phi })& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }}}{\int }_{\mathrm{0}}^{\mathit{\phi }}{\int }_{r_{\mathrm{1}}}^{r_{\mathrm{2}}}{W}_r(h,\mathit{\theta })\cdot \text{d}r\cdot \text{d}{\mathit{\phi }}^{\prime }\\ {\displaystyle }& {\displaystyle }={\displaystyle \frac{\mathit{\phi }}{\mathrm{2}\mathit{\pi }}}{\int }_{r_{\mathrm{1}}}^{r_{\mathrm{2}}}{W}_r(h,\mathit{\theta })\cdot \text{d}r.\end{array}\end{array}$$

The contribution area of the grassland meadow and surrounding patches is roughly equivalent to a circle of radius r₂≈20 m. Hence, the portion of measured neutrons from this area is $n(\mathrm{0},r_{\mathrm{2}})\approx \mathrm{41}\pm \mathrm{2}$ %, depending on h and θ. The dry and sealed areas beyond the grass meadow are effectively damping the otherwise highly dynamic signal from the soil (orange line in Fig. 9).

To remove this damping effect, we suggest a new method to rescale the dynamic component of the neutron signal that is influenced by both a variable and a constant patch in the footprint. At the urban test site, only 0.1 ha of the footprint contains soil, beyond which everything else is either paved area or solid building. Thus, only a small fraction $n(r_{\mathrm{1}},r_{\mathrm{2}},\mathit{\phi })$ of the total neutrons is connected to soil moisture variability. In order to compare these measurements with independent soil moisture sensors, we introduce an areal correction,

$$\begin{array}{}\text{(11)}& N_{\text{corr}}={\displaystyle \frac{N-〈N〉}{n(r_{\mathrm{1}},r_{\mathrm{2}},\mathit{\phi })}}+〈N〉,\end{array}$$

that essentially scales the anomaly of neutrons by the inverse fraction of the contributing area, where 〈⋅〉 denotes the temporal mean. Using the corrected data from the CRNS probe (blue line) and the average soil moisture from the two profiles (grey), Fig. 9 demonstrates that this scaling approach brings both signals into good agreement and is therefore helpful to interpret CRNS data with confined areal coverage.

Besides the improved match of soil moisture dynamics, the area-corrected signal apparently overestimates soil moisture peaks during and after rain events. This can be interpreted as a representation of an important hydrological feature in urban areas. When the whole footprint is considered for data interpretation, it becomes evident that the CRNS should be sensitive to precipitation water ponded on buildings and paved ground before it eventually evaporates. Therefore, the additional water seen by the CRNS probe following rain events can be suspected of representing the intercepted water over sealed areas.

4 Summary and conclusion

This intercomparison study was motivated by the observation of unknown variability in CRNS data and by the aim to understand how reliable and reproducible soil moisture data could be generated using the method of cosmic-ray neutron sensing. To address the open questions, we co-located nine CRNS measurement stations within a 5 m ×15 m grassland area, surrounded by complex urban terrain. Three main hypotheses were investigated and the following conclusions were drawn:

• A.

  We claimed that the sensor location has an influence on the neutron measurement. The hypothesis was tested by swapping the position of four out of nine CRNS probes. We found the influence on the neutron counts is measurable, but insignificant within a few metres. However, mobile surveys as well as neutron simulations indicated that neutron abundance can be highly heterogeneous within the sensor's footprint, making the signal prone to local effects on scales above a few metres.

• B.

  Device-specific differences were suspected of being responsible for systematic variations in the CRNS signal. This was tested with the help of the manufacturers by consistently adjusting neutron detection parameters and aligning the pulse height spectra of the nine sensors. The detection parameters were found to have significant influence on the count rate by up to 3 %. The adjustment led to a reduction of the total contribution of systematic errors down to the order of the statistical counting errors. We recommend applying this adjustment in order to achieve consistent measurements among sensors.

• C.

  Statistical noise was suspected to be the reason for much of the remaining variability that hinders comparability of neutron signals. We applied temporal aggregation to the neutron signals and looked at the correlation and ensemble spread of the CRNS products. Sensors showed correlations below 0.6 for hourly data and above 0.9 for aggregation of 6 h and beyond. In the same manner the RMSE between the soil moisture products improved from 2 % down to 0.9 % gravimetric percent. If multiple standard CRNS detectors are required to deliver similar results under similar conditions, a minimum temporal resolution of 6 h was found to provide acceptable comparability for humid climate at sea level. This value can be considered as an upper limit, as it gets further reduced by drier climates, higher altitudes, and more sensitive detectors.

This work highlights the importance of studies on sensor-to-sensor intercomparison for geoscientific instruments. Those efforts can reveal unexpected features or systematic errors, can highly improve the understanding of the sensor response, and will thus improve their application in environmental sciences. One of the impacts of this study has already led to improved efforts to adjust the detection parameters during the manufacturing process.

The CRNS water equivalent measured in the urban environment has shown remarkable agreement with independently measured soil moisture profiles when accounted for the sealed-area effect. With the proposed “areal correction” approach the influence of sealed (and thus constantly dry) areas in the footprint can be quantified and the corresponding damping effects removed. The quantification of the sensitivity to local patches in the footprint is particularly meaningful for supporting hyper-resolution land surface modelling (e.g. Chaney et al., 2016) and precision agriculture. The latter includes targeted irrigation based on information about soil properties, plant variety, and density (Hedley et al., 2013; Pan et al., 2013). In addition to soil moisture, the CRNS probe appeared to be sensitive to intercepted water over sealed areas. Such information could be used to actually quantify interception and evaporation processes (see e.g. Baroni and Oswald, 2015) and could eventually contribute to closing the water balance.

In future studies we would recommend to further assess the potential of cosmic-ray neutron sensors for urban hydrology. Since water in complex terrain is almost impossible to quantify with point sensors, the large-scale averaging capabilities of cosmic-ray neutron probes could be a promising advantage for urban sciences.